Законы массопереноса

Основные понятия массопереноса

Многие процессы теплообмена, происходящие в природе и технике, сопровождаются внешним и внутренним массообменом. При этом пред­полагается, что химических реакций между компонентами нет. Напри­мер, испарившаяся жидкость, распространяясь путем диффузии в парогазовой среде, будет изменять интенсивность теплоотдачи в этой среде. При тепловлажностной обработке бетона происходят конденса­ция пара и его испарение с поверхности изделий, миграция влаги, паров и воздуха внутри этих изделий. Конденсация пара на открытых поверхностях изделий может привести к переувлажнению поверхност­ных слоев бетона, а испарение влаги с этих поверхностей - к его пересушиванию. Все это в конечном счете может ухудшить качества бето­на (прочность, морозостойкость, долговечность и т. п.). Массообмен (диффузия) лежит в основе таких физических и химических процессов, как адсорбция вещества из растворов, сублимация, окисление, горение, разделение изотопов, цементирование металлических изделий и т.д.

Законы массопереноса

Между процессами тепло- и массообмена существует аналогия, ос­нованная на общности механизма переноса энергии и массы. Поэтому основные законы массо- и теплообмена имеют одинаковые выражения. Например, аналогично закону Фурье, определяющему вели­чину потока теплоты, поток массы одного из компонентов вследствие молекулярной (концентрационной) диффузии определяется законом Фика, связывающим массоперенос с полем концентрации:

j = -Ddс/dn = -D grad c, (1)

где j - массоперенос, т. е. плотность диффузионного потока массы вещества, моль/(м²с); D - коэффициент диффузии, м²/с; dc/dn - градиент концентрации, моль/(м³×м).

Поскольку при расчете газовых смесей принято концентрацию с выражать через парциальное давление компонента по ра­венству с = p/R₀T = n/V, то выражение (1) можно записать в форме

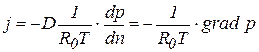. (1')

Из уравнения (1') наиболее наглядно видно влияние температу­ры газовой смеси на массоперенос.

При стационарности процесса и постоянстве коэффициента диффу­зии D аналогично дифференциальному уравнению переноса энергии движущейся жидкости выводится дифференциальное уравнение Фика, отражающее материальный баланс диффундирующего вещест­ва в условиях вынужденного движения:

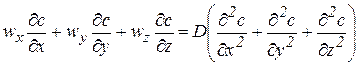. (2)

Коэффициент диффузии D в этом уравнении аналогичен температу­ропроводности а и характеризует интенсивность изменения концентрации.

В условиях турбулентного движения жидкости вместо молекуляр­ной диффузии возникает турбулентная. В этом случае уравнения (1) и (2) по форме написания сохраняются, но под концентрациями и компонентами скоростей нужно понимать их усредненные по време­ни значения. Коэффициент D в этом случае называется турбулентным коэффициентом диффузии, который во много раз превышает молеку­лярный коэффициент диффузии.

В условиях турбулентного течения аналогично формированию ди­намического пограничного слоя неодинаковая концентрация на внут­ренней его границе и вне его приводит к образованию диффузионного пограничного слоя. Если по аналогии с коэффициентом теплоотдачи a ввести понятие о коэффициенте массоотдачи b, то

j = bDс, (4)

где Dс - разность концентраций в потоке и у стенки; b - коэффициент массоот­дачи, м/с, представляющий собой плотность диффузионного потока массы вещест­ва при разности концентраций этого вещества в потоке и у стенки, равной единице.

Для газовых смесей уравнение (4) более удобно записать с уче­том парциального давления компонента в форме

j = bDp/R₀T (4')

По аналогии с уравнением -l×dt/dn = αDt условие массопереноса на границе потока выразится равенством

bDc = D(dc/dn). (5)

Поскольку в уравнение диффузии (2), как и в уравнение пе­реноса энергии, входят составляющие скорости w_x, w_y и w_z, то система уравнений (2) и (5) должна быть дополнена урав­нениями движения, сплошности потока, а также усло­виями однозначности, дающими описание всех частных особенностей рассматриваемого явления.