Расчет коэффициентов теплопередачи
Коэффициент теплопередачи для первого корпуса определяют по уравнению аддитивности термических сопротивлений:
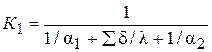 .
.
Примем, что суммарное термическое сопротивление равно термическому coпротивлению стенки δст/λст и накипи δн/λн. Термическое сопротивление загрязнений со стороны пара не учитываем. Получим:
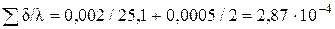 (
( 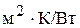 ).
).
Коэффициент теплоотдачи от конденсирующегося пара к стенке α1 находится по уравнению (3.16):

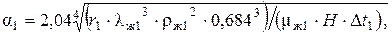
где r1—теплота конденсации греющего пара, Дж/кг; ρж1, λж1, μж1 —соответственно плотность (кг/м3), теплопроводность (Вт/(м·К)), вязкость (Па с) конденсата при средней температуре пленки tпл=tг1-Δt1/2, где Δt1— разность температур конденсации пара и стенки, град.
Расчет α1, ведут методом последовательных приближений. В первом приближении примем разность температур конденсации пара и стенки Δ 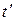 1 =2,0 оС. Тогда
1 =2,0 оС. Тогда
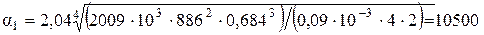
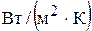
Из уравнения (3.22) находится перепад температур на стенке:
Δtст= α1 Δ 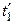 ∑δ/λ=10500
∑δ/λ=10500 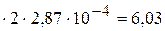 оС.
оС.
И разность температур конденсации пара и стенки со стороны раствора и его температурой кипения Δ 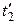 :
:
Δ 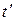 2= Δt1- Δtст - Δ
2= Δt1- Δtст - Δ 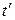 1=13,13-6,03-2=5,1 оС.
1=13,13-6,03-2=5,1 оС.
Распределение температур в процессе теплопередачи от пара через стенку к кипящему раствору показано на рис. 4.4.
Коэффициент теплоотдачи от стенки к кипящему раствору α2, для пузырькового кипения в вертикальных кипятильных трубках при условии естественной циркуляции раствора находиться по уравнению (3.17):
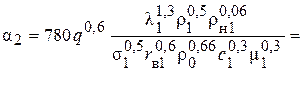
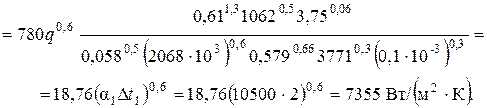
Физические свойства кипящих растворов КОН и их паров из табл.4.2 приведены (табл. П1, П2, П27-П30):
Таблица 4.2
| Параметр | Корпус | ||
Теплопроводность раствора λ, Вт/ 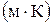
| 0,61 | 0,62 | 0,69 |
| Плотность раствора ρ, кг/м3 | |||
Теплоемкость раствора с, Дж/ 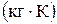
| |||
Вязкость раствора μ, 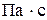
| 0,1 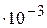
| 0,29 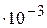
| 0,7 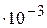
|
| Поверхностное натяжение σ, Н/м | 0,058 | 0,066 | 0,099 |
| Теплота парообразования rв, Дж/кг | 2068 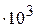
| 2148 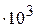
| 2372 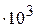
|
| Плотность пара ρн, кг/м3 | 3,75 | 2,0 | 0,098 |
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
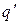 = α1 Δ
= α1 Δ 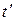 1=10500
1=10500 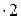 = 21000 Вт/м2;
= 21000 Вт/м2;
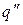 = α2 Δ
= α2 Δ 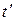 2=7355
2=7355 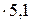 = 37510 Вт/м2.
= 37510 Вт/м2.
Как видим, 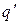
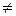
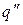 .
.
Для второго приближения примем Δ 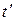 1 = 3,0 оС.
1 = 3,0 оС.
Пренебрегая изменением физических свойств конденсата при изменении температуры на 1,0 оС, рассчитаем α1 по соотношению:
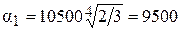 Вт/(м2·К)
Вт/(м2·К)
Получим:
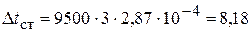 оС;
оС;
Δt2=13,13-3-8,18=1,95 оС;
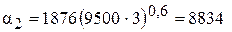 Вт/(м2·К);
Вт/(м2·К);
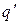 =9500
=9500 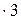 = 28500 Вт/м2;
= 28500 Вт/м2; 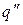 =8834
=8834 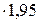 = 17220 Вт/м2.
= 17220 Вт/м2.
 |
Очевидно, что
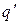
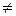
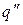 .
.
Рис. 4.4. Распределение температур в процессе теплопередачи от пара к кипящему раствору через многослойную стенку: 1 - пар; 2 - конденсат; 3 – стенка; 4 – накипь; 5 – кипящий раствор

Рис. 4.5. Зависимость удельной тепловой нагрузки q от разности температур Δ 
Для расчета в третьем приближении строим графическую зависимость удельной тепловой нагрузки q от разности температур между паром и стенкой в первом корпусе (рис. 4.3) и определяем Δ 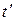 1=2,6 оС. Получим:
1=2,6 оС. Получим:
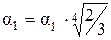
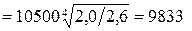 Вт/(м2·К);
Вт/(м2·К);
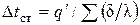
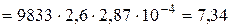 оС;
оС;
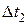
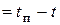 кип =13,13-2,6-7,34=3,19 оС;
кип =13,13-2,6-7,34=3,19 оС;
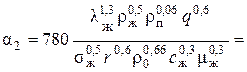
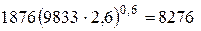 Вт/(м2·К);
Вт/(м2·К);
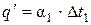 =9833
=9833 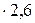 = 25570 Вт/м2;
= 25570 Вт/м2; 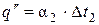 =8276
=8276 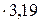 = 2640Вт/м2.
= 2640Вт/м2.
Как видим, 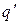
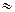
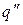 .
.
Если расхождение между тепловыми нагрузками не превышает 3 %, расчет коэффициентов α1 и α2 на этом заканчивают. Находим К1, 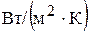 :
:
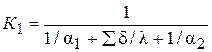 =1/(1/9833+2,87
=1/(1/9833+2,87 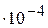 +1/8276)=1963
+1/8276)=1963 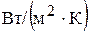 .
.
Далее рассчитаем коэффициент теплопередачи для второго корпуса К2 , 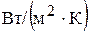 . Для этого найдем:
. Для этого найдем:
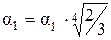
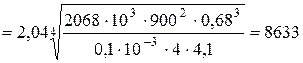
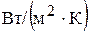 ;
;
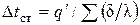
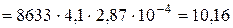 оС;
оС;
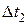
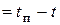 кип =19,56-4,1-10,16=5,3 оС;
кип =19,56-4,1-10,16=5,3 оС;
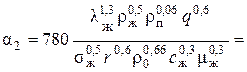
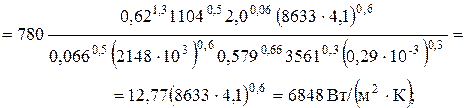
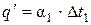 = 8633
= 8633 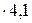 = 35395 Вт/м2;
= 35395 Вт/м2;
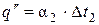 = 6848
= 6848 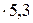 = 36294 Вт/м2.
= 36294 Вт/м2.
Как видим, 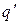
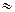
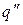 .Определим К2:
.Определим К2:
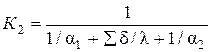
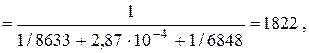
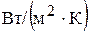 .
.
Рассчитаем теперь коэффициент теплопередачи для третьего корпуса К3, найдем:
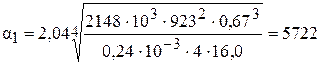
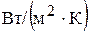 ;
;
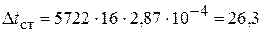 оС;
оС;
Δt2 = 53,17-16,0-26,3=10,87 оС;
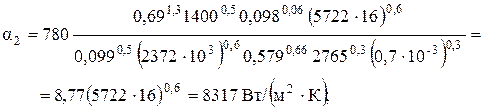
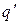 =5722
=5722 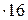 = 91550 Вт/м2;
= 91550 Вт/м2; 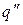 = 8317
= 8317 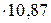 = 90410 Вт/м2.
= 90410 Вт/м2.
Как видим, 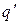
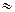
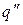 . Найдем К3:
. Найдем К3:
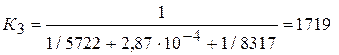
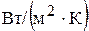 .
.
Дата добавления: 2016-05-28; просмотров: 5035;











