аналитические выражения
В общем случае, рассматривая рабочее тело как термодинамическую систему, можем сформулировать первый закон термодинамики:
изменение энергии системы, численно равно сумме мер взаимодействии с окружающими телами
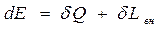 (3-16)
(3-16)
где dE - элементарное изменение полной энергии рабочего тела;
dQ - элементарное количество подведённого тепла;
dLвн - элементарная работа, совершенная внешними телами над рабочим телом.
Для рабочих тел кинетическая энергия которых и ее изменение невелики можно записать
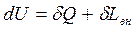 (3-17)
(3-17)
или
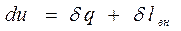 (3-17а)
(3-17а)
Для исследования процессов преобразования тепла в работу используется выражение первого закона термодинамики в форме
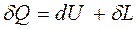 (3-18)
(3-18)
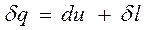 (3-18а)
(3-18а)
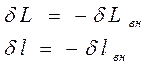
где dL и d l - работа, совершённая рабочим телом над окружающими телами.
"Тепло, подведенное к рабочему телу, идет на совершение работы и изменение внутренней энергии".
Для конечного процесса
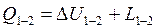 (3-19)
(3-19)
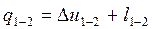 (3-19а)
(3-19а)
где: 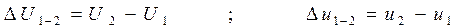

Если протекает процесс при постоянном объёме - изохорный процесс, то
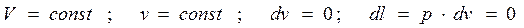
тогда из (1-17), получим
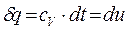 (3-20)
(3-20)
или. полагая сv=const для конечного процесса
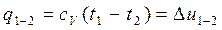 (3-20а)
(3-20а)
т.е. всё тепло в изохорном процессе идёт на изменение внутренней энергии. Последний вывод позволяет всякое изменение внутренней энергии численно определять как тепло, подведённое в изохорном процессе.
Найдем аналитическое выражение I-oго закона термодинамики через энтальпию h, для чего продифференцируем выражение
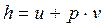
откуда 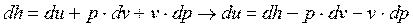
Подставляя последнее выражение в (3-18а), получим
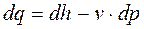 (3-21)
(3-21)
Интегрируя (3-21) от состояния I до состояния 2, получим
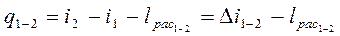 (3-22)
(3-22)
где 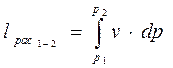
Величина lрас носит название располагаемой работы. Если протекает процесс при постоянном давлении - изобарный процесс, то
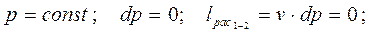
тогда из (3-21) получим
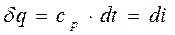 (3-23)
(3-23)
или полагая cp=const для конечного процесса
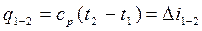 (3-23а)
(3-23а)
т.е. все тепло в изобарном процессе идет на изменение энтальпии рабочего тела. Последний вывод позволяет всякое изменение энтальпии численно определять как тепло, подведённое в изобарном процессе.
Первый закон термодинамики позволяет получить зависимости для измерения энтропии в произвольных обратимых процессах для чего из определения энтропии выразим и подставим в (3-19а)
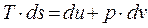 или
или 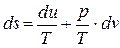
Заменяя 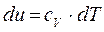
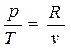
получим 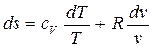
Интегрируя последнее выражение от начального состояния (1) до конечного состояния (2) найдём
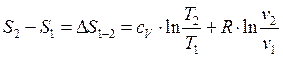 (3-24)
(3-24)
Записав уравнение состояния для состояний 1 и 2, найдём
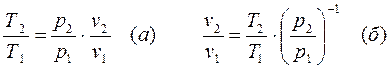
Подставив в (а) получим (3-24)
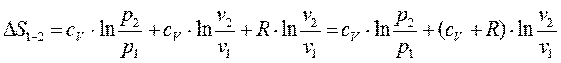
Или в окончательном виде
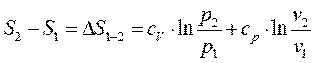 (3-25)
(3-25)
Подставив б в (3-24) после преобразования получим
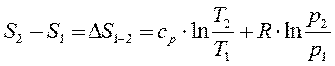 (3-26)
(3-26)
Зависимости (3-24) ¸ (3-26) справедливы для любых обратимых процессов.
Дата добавления: 2018-11-26; просмотров: 1042;











