Аналитические методы

К аналитическим относятся классический метод непосредственного интегрирования и метод источников.

В качестве примера использования классического метода рассмотрим технологический процесс иглофрезерования поверхностей металлической щеткой (рис.3.1).

Инструмент представляет собой массивный корпус, снабженный большим количеством жестких металлических проволочек (игл).

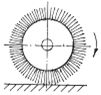
Рис. 3.1 – Схема процесса иглофрезерования

Стойкость такого инструмента зависит от интенсивности износа каждой проволочки, который определяется в большой степени температурой её в процессе обработки.

Схематизируем процесс (рис.3.2)

- Представим иголку как стержень, ограниченный с двух сторон;

- Плотность q теплового потока на торце иголки распределена равномерно;

- Температура на верхнем торце (x = l) равна температуре Θ₀ корпуса инструмента;

- Принимаем тепловой процесс установившимся;

- Боковые поверхности иголки адиабатичны, т.е. теплообмен с окружающей средой отсутствует, q_S = 0;

- Принимаем, что коэффициент теплопроводности λ = const, т.е. не зависит от температуры материала.

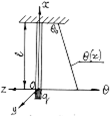
Рис. 3.2 – Распределение температур в стержне

Размеры торца иголки по сравнению с ее длиной существенно меньшие, что позволяет принять допущение о небольшом изменении температуры в направлении осей y и z, т.е. рассматривать задачу с одномерным температурным полем.

Дифференциальное уравнение теплопроводности для одномерного стационарного температурного поля.(1.25) имеет вид

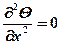
Дифференцируя это уравнение первый раз, получаем

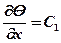, откуда .

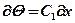Интегрируя второй раз, получаем

Θ(х) = С₁х + С₂ (3.1)

Для определения постоянных интегрирования используем начальные условия

При x = 0 в соответствии с законом Фурье (1.9)

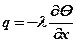или

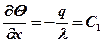
При x = l из (3.1) С₂ = Θ(х) – С₁х, температура Θ(х) = Θ₀,

Тогда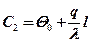

Таким образом

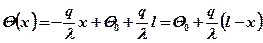(3.2)

Это и есть решение дифференциального уравнения (1.25) для задачи с одномерным температурным полем при принятых допущениях. Уравнение (3.2) представляет собой прямую линию (рис.3.2)

Если же принять, что коэффициент теплопроводности зависит от температуры, то решение дифференциального уравнения существенно усложняется. Еще более сложным оказывается решение для двумерных и трехмерных задач при более сложной форме тел. Это приводит к тому, что классический метод применяют сравнительно редко.

Основные положения метода источников состоят в следующем:

1.Источник теплоты любой формы, движущийся или неподвижный, действующий в течение любого промежутка времени может быть представлен как система точечных мгновенных источников теплоты.

2.Процесс распространения теплоты в теле ограниченных размеров может быть представлен как процесс распространения теплоты в неограниченном теле, если фактические источники теплоты дополнить системой фиктивных источников. Это положение называется принципом отражения источников.

Основные положения метода разработаны Рыкалиным Н.Н. Он использовал математическое выражение, описывающее температурное поле, которое возникает под действием мгновенного точечного источника теплоты в неограниченном теле, которое было получено лордом Кельвином. Код такой задачи , а формула имеет вид

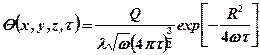, (3.3)

где Q – количество теплоты, внесенное в тело источником,

τ – время, прошедшее от момента теплового импульса,

λ, ω – коэффициенты теплопроводности и температуропроводности материала тела,

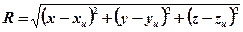– расстояние от места

вспышки до рассматриваемой точки,

x_u, y_u, z_u – координаты источника,

x,y,z – координаты рассматриваемой точки.

Рыкалин показал, что процесс распространения теплоты в полупространстве 1 (рис.3.3) от действия источника I можно представить как часть процесса в неограниченном пространстве 2, но с дополнительным источником теплоты I_l. Источник, расположенный на адиабатической поверхности А полупространства, вызывает в нем температуру в 2 раза большую, чем такой же источник в неограниченном пространстве.

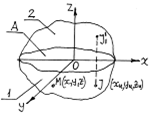
Рис. 3.3 – Схема отраженных источников

Как перейти от формулы (3.3) к описанию температурных полей от действия реальных источников теплоты?

Для этого необходимо произвести следующие интегральные переходы.

1-й переход – от точечного к одно-, дву- и трехмерному источнику:

- Одномерный (линейный) – бесконечное множество точечных источников, поставленных рядом и действующих одновременно.

- Двумерный – совокупность множества точечных, занимающих площадку поверхности и действующих одновременно.

- Трехмерный – совокупность множества точечных, занимающих некоторый объем и действующих одновременно.

2-й переход – от мгновенного источника к действующему непрерывно. Непрерывное действие имитируется серией мгновенных импульсов, действующих друг за другом с бесконечно большой частотой.

3-й переход – от мгновенного источника к движущемуся. Движение источника имитируется рядом последовательных вспышек мгновенных импульсов, последовательно возникающих по траектории перемещения источника.

Осуществляя эти переходы, можно получить формулы для определения температурных полей в различных тепловых задачах.

Для примера приведем некоторые решения тепловых задач.

1-й переход – от мгновенного точечного источника к мгновенному любой другой конфигурации.

Код задачи 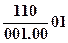– источник одномерный, прямой, неограниченный, с равномерным распределением по оси x, действующий в неограниченном теле при ГУ1.

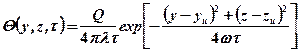. (3.4)

Код задачи 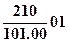– источник двумерный, плоский, неограниченный, с равномерным распределением по осям x и y в неограниченном теле при ГУ1.

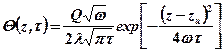. (3.5)

2-й переход – от мгновенного точечного источника к непрерывно действующему неподвижному.

Код задачи 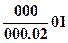– источник точечный, действующий в неограниченном теле в течение длительного времени при ГУ1.

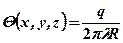, (3.6)

где R – расстояние от источника до рассматриваемой точки.

Код задачи 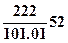– источник двумерный круговой с равномерным распределением, неподвижный, действующий некоторое время на стержне, ограниченном с одной стороны при ГУ2.

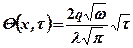(3.7)

3-й переход – от мгновенного точечного к движущемуся, действующему некоторое время.

Код задачи – источник двумерный, полосовой, ограниченный по одной оси, с равномерным распределением, быстродвижущийся, действующий длительное время в неограниченном теле с ГУ2.

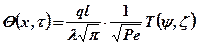, (3.8)

где Т(ψ, ζ) специальная функция, приводится в литературе в виде таблиц или графиков.

Для других тепловых задач формулы приводятся в литературе [1].