Смеси идеальных газов

Идеальный газ. Уравнение состояния

Под идеальным газом понимают газ, в котором полностью отсутствуют силы межмолекулярного взаимодействия, а молекулы можно считать материальными точками.

Для такого газа справедливо уравнение состояния Клапейрона - Менделеева

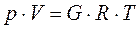(3-1)

где V и G - объём и масса газа;

R - газовая постоянная данного газа.

Газовая постоянная определяется выражением

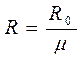(3-2)

где m - молекулярная масса данного газа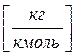

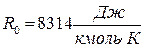- универсальная газовая постоянная.

Реальные газы при достаточно высоких температурах и малых плотностях хорошо соответствуют модели идеального газа, а такие условия очень широко распространены в технике.

Смеси идеальных газов

В тоже время в технике очень редко приходится иметь дело с чистыми газами. В большинстве случаев рабочие тела представляют собой газовые смеси, под которыми понимают механическую смесь нескольких газов - компонентов химически между собой не взаимодействующих.

В соответствии с определенней идеального газа можно считать, что каждый компонент газовой смеси ведет себя так, как будто других компонентов нет, т.е. каждый компонент равномерно заполняет объём смеси V и оказывает на стенки давление p_i ; которое называется парциальным давлением. Очевидно, что все компоненты в смеси имеют одинаковую температуру Т .

Давление газовой смеси определяется законом Дальтона, который гласит: "Давление газовой смеси при отсутствии химических реакций равно сумме парциальных давлений компонентов, составляющих смесь''.

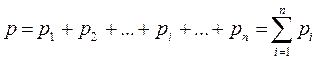(3-3)

Поскольку каждый компонент смеси подчиняется уравнению состояния идеального газа, то и вся смесь должна подчиняться этому уравнению, которое можно представить в виде

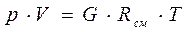(3-4)

где G и R_см - масса и кажущаяся газовая постоянная смеси, для которой будем считать справедливым соотношение (3-2), которое для смеси примет вид

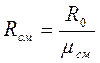(3-2а)

где m_см - кажущаяся молекулярная масса смеси,

Как видим, чтобы использовать в термодинамических расчётах уравнение (3-4) необходимо знать величину R_см или m_см, которые отвечают данному составу смеси.

Состав смеси может быть задан тремя способами: с помощью массовых, объёмных и мольных долей.

I. Массовое задание состава смеси, когда заданы массовые доли компонентов g_i:

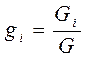(3-5)

где G_i - масса i -того компонента в смеси.

Очевидно, что

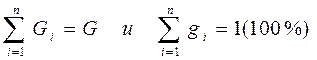(3-6)

2. Объемное задание состава смеси, когда заданы объёмные доли компонентов r_i :

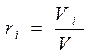(3-7)

где V_i - парциальный объём компонента - объём который имел бы компонент, если бы один находился под давлением смеси и имел температуру смеси.

Очевидно, что

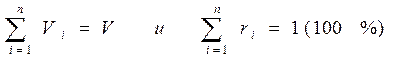(3-8)

Запишем уравнение состояния i - ого компонента при температуре смеси

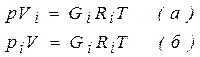
Разделив выражение (б) на (а), получим

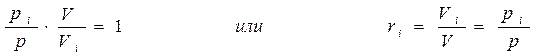
2. Мольное задание состава смеси, когда заданы мольные доли компонентов n_i:

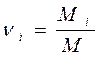(3-9)

где M_i и M - количество молей i - го компонента и общее количество молей в смеси.

Выразим парциальный объем V_i - го компонента и объём смеси через мольный объём и количество молей

(в) (г)

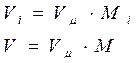
Разделив выражение (г) на (в), получим:

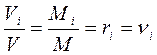
т.е. мольная доля идеального газа численно равна объёмной доле, поэтому в дальнейшем будем оперировать только с объёмными долями.

Найдём взаимосвязь между массовыми и объёмными долями компонента:

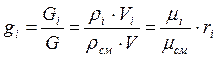,т.е.

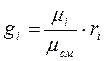(3-10)

Из зависимости (3-2) можно получить

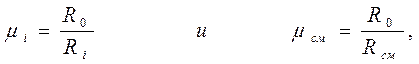
тогда

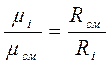(д)

Подставив выражение (д) в (3-10), получим

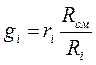(3-11)