Примеры сетевых задач, сводящихся к задачам линейного программирования

Напомним, прежде всего, постановку задачи линейного программирования. Требуется найти экстремум линейной функции, на аргументы которой наложены линейные ограничения.

Таким образом, задачи линейного программирования (ЗЛП) относятся к задачам на условный экстремум. Однако для исследования линейной функции многих переменных на условный экстремум нельзя применять хорошо разработанные методы математического анализа.

Действительно, пусть

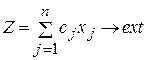
при линейных ограничениях

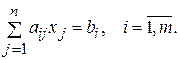
Необходимым условием экстремума является равенство нулю частных производных

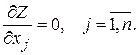
Но эти частные производные от линейной функции равны константам

,

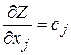Отсюда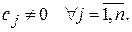

Так как все коэффициенты линейной функции не могут быть равны нулю, то внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть только на границе области.

Поэтому для подобных задач разработаны специальные методы линейного программирования.

Рассмотрим вначале формы записи задач линейного программирования.

Модель задачи линейного программирования может быть записана в одной из приведенных ниже форм:

1. Общая или произвольная форма записи

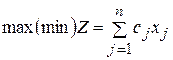
при ограничениях

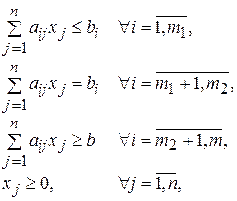
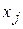– произвольные .

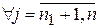2. Симметричная или стандартная форма записи

а)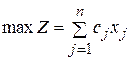

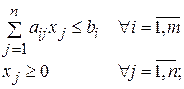
б)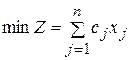

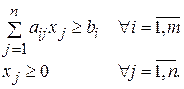
3. Каноническая или основная форма записи

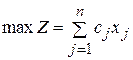
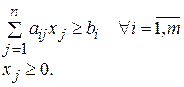
Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме.

Таким образом, если имеется способ решения ЗЛП в одной из приведенных форм, то тем самым может быть определен оптимальный план задачи в любой другой форме. В этом случае говорят о стратегической эквивалентности ЗЛП в любой из форм.

Так, при необходимости задачу минимизации можно заменить задачей максимизацией и наоборот:

.

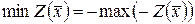Неравенство типа 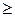путем умножения левых и правых частей на -1 можно превратить в неравенство типа 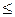и наоборот.

Ограничения-неравенства типа

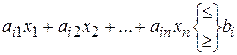
преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных :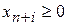

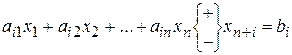
Если в ЗЛП какая-либо переменная 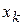не подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных 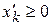и :

.

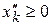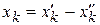Далее рассмотрим геометрическую интерпретацию задачи линейного программирования применительно к двум переменным.

Найти оптимальный план 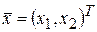, доставляющий

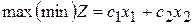(1)

при ограничениях

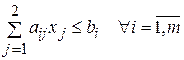(2)

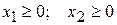(3)

Начнем с геометрической интерпретации области допустимых решений.

Каждые из неравенств (2) определяет на координатной плоскости 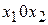некоторую полуплоскость, а система неравенств (2), (3) в случае ее совместности – их пересечение.

Это множество будет выпуклым. Оно может представлять собой следующие геометрические конструкции (Рисунок 28).

Перейдем далее к геометрической интерпретации целевой функции (1).

Уравнение 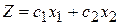при фиксированном значении 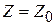определяет на плоскости прямую линию

.

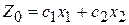При изменении 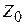получается семейство параллельных линий, называемое линиями уровня.

а)		выпуклый многоугольник (число вершин равно m);
б)		неограниченная выпуклая многоугольная область;
в)		отрезок прямой;
г)		луч;
д)		точка;
е)		пустое множество.

Рисунок 28 – Геометрическая интерпретация ЗЛП

Вектор 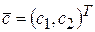с компонентами из коэффициентов пр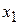и и 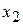перпендикулярен к каждой из линий уровня.

Вектор 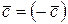показывает направление возрастания (убывания) целевой функции.