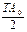Классы точности подшипников

Качество подшипников качения при прочих равных условиях определяется точностью присоединительных размеров D, d, В и тел качения, и точностью вращения, характеризуемой радиальным и осевым биением дорожек качения и торцов колец.

В зависимости от указанных показателей точности по СТ СЭВ 774 – 77 установлено пять классов точности подшипников: 0, 6, 5, 4, 2. Самый точный – 2-й класс, у которого точностые показатели в 10 раз выше, чем у нулевого класса.

Класс точности подшипника выбирают исходя из степени точности механизма в целом и условий его работы.

0 и 6 классы применяют в общем машиностроении в узлах нормальной и повышенной точности, причём 6-й класс применяют при больших частотах вращения валов.

5 и 4 классы применяют в станкостроении, причём 4 – в прецизионных станках.

2 класс применяют в особо точных изделиях (гироскопы, космическая техника).

Пример обозначения подшипников 6 – 205, где 6 – класс точности, 205 – серия.

Поля допусков колец подшипников качения

r

L

B

По СТ СЭВ 774 – 77

Для сокращения номенклатуры подшипники качения изготовляют с отклонениями размеров колец, не зависящими от посадок, по которым их будут монтировать.

Отклонения зависят только от класса точности и величины размеров колец.

Для всех классов точности верхнее предельное отклонение присоединительных диаметров принято равным нулю.

Т. е. наружное кольцо является основным валом, а внутреннее – основным отверстием. Но в отличии от основного отверстия в гладких цилиндрических соединениях поле допуска на внутреннее кольцо подшипника зеркально перевёрнуто вниз. Вследствие этого, обычные переходные посадки в сочетании с таким полем допуска дают, как правило, только натяги.

Поля допусков колец подшипников буквами не обозначают т.к. их отклонения определяются по специальному ГОСТу СТ СЭВ 774 – 77.

Посадки нужно выбирать так, чтобы вращающееся кольцо подшипника было смонтировано с натягом, исключающим возможность обкатки или проскальзывания этого кольца по посадочной поверхности вала или отверстия в корпусе в процессе работы под нагрузкой; другое кольцо нужно монтировать с зазором.

Исходя из этого:

1. при вращающемся вале необходимо иметь неподвижное соединение внутреннего кольца с валом; наружное кольцо соединить с корпусом с небольшим зазором;

2. при неподвижном вале внутреннее кольцо должно иметь посадку на валу с небольшим зазором, а наружное кольцо – неподвижную в корпусе.

Рекомендуемые поля допусков и примеры их применения приведены в СТ СЭВ 773 – 77.

С зазором монтируют то кольцо, которое испытывает местное нагружение; при такой посадке устраняется заклинивание шариков, а кольцо, смонтированное с зазором под действием толчков и вибрацией постепенно поворачивается по посадочной поверхности, благодаря чему износ беговой дорожки происходит равномерно по всей окружности кольца, что увеличивает срок службы подшипника

Также с зазором монтируется кольцо подшипника, испытывающее колебательное нагружение.

Рекомендуемые посадки с зазором выбирают по табл. 4.76 и 4.84 (Мягков).

Монтаж подшипника с натягом производят преимущественно по тому кольцу, которое испытывает циркуляционное нагружение.

Поэтому, в обозначении подшипниковых посадок записывают только поле допуска отверстия под наружное кольцо подшипника или вала под внутреннее кольцо.

Например, Ø50Н7 – для наружного кольца, Ø36m9 – для внутреннего кольца.

Выбор посадок подшипников качения на валы и в корпуса

Посадку подшипников качения на вал и в корпус выбирают в завсимости от типа подшипника (радиальный, радиально-упорный, упорный), его размера, условий его эксплуатации, величины и характера действующих на него нагрузок и вида нагружения колец.

В соответствии с СТ СЭВ 773 – 77 различают три основных вида нагружения колец: местное, циркуляционное, колебательное

При местном нагружении кольцо воспринимает постоянную по направлению результирующую радиальную нагрузку F_r одним и тем же ограниченным участком окружности дорожки качения и передаёт её соответствующему ограниченному участку посадочной поверхности вала или корпуса, что имеет место, например, когда кольцо не вращается относительно нагрузки.

При циркуляционном нагружении кольцо воспринимает результирующую радиальную нагрузку F_r последовательно всей окружностью дорожки качения и передаёт её также последовательно всей посадочной поверхности вала или корпуса. Такое нагружение кольца получается при его вращении относительно постоянно-направленной нагрузку F_r или наоборот, при радиальной нагрузке, вращающейся относительно рассматриваемого кольца.

При колебательном нагружении вращающееся кольцо воспринимает равнодействующую нагрузку F_r+с двух радиальных нагрузок (одна F_r – постоянная по направлению, а другая F_с – меньшая по величине, вращается) ограниченным участком окружности дорожки качения и передаёт её соответствующему ограниченному участку посадочной поверхности вала или корпуса. Равнодействующая нагрузка F_r+с не совершает полного оборота, а колеблется в пределах некоторого сектора.

ЛЕКЦИЯ 13

Взаимозаменяемость зубчатых передач.

Зубчатые передачи - это сложные кинематические пары, которые имеют ряд назначений, а именно: передача крутящих| моментов, смены направления движения, смены частоты вращения, преобразования вращательного движения в поступательное и наоборот.

Классифицируются зубчатые передачи по таким признакам:

назначением/кинематические, скоростные, силовые, общего назначения/;

формой детали/цилиндрические, конические, гипоидные, червячные/;

направлением зуба/прямо- и косозубые, шевронные/;

формой зуба/эвольвентные, циклоидные, дуга круга/.

Геометрические параметры зубов зубчатых колес стандартизированы. Самые распространенные в промышленности зубчатые колеса с эвольвентным| профилем зуба, ГОСТ 13755-81 /СТ СЭВ| 308-76/.

Система допусков цилиндрческиих зубчатых кольев.

Параметры точности регламентируют точность отдельного колеса и эксплуатационные параметры передачи за ГОСТ 1643-81 /СТ СЭВ 641-77, СТ СЭВ 642-77/.

Установлено 12 степеней точности зубчатых колес и передач: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 /ступени 1 и 2 - перспективные/.

Применение передач с различными степенями точности:

3...5 - в контрольно-измерительных приборах;

5...7 - в станках;

6...9 - в автомобилях и тракторах, сельскохозяйственных машинах;

9...12 - в подъемно-транспортных машинах.

Для каждой степени точности установлены нормы допустимых отклонений параметров, которые определяют кинематическую точность, плавность работы и контакт зубов /нормы кинематической точности, плавности работы, контакта зубов/.

Нормы кинематической точности.

Кинематические погрешности колеса и передачи ограничиваются.

1. Наибольшая кинематическая погрешность зубчатого колеса - это наибольшая алгебраическая разность значений кинематической погрешности зубчатого колеса в пределах угла j /полного оборота/:

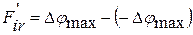/1.72/

где 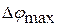, 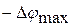- соответственно наибольшая положительная и отрицательная погрешность угла. График кинематической погрешности изображен на рис.1.69.

2. Накопленная погрешность шага зубчатого колеса 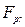наибольшая алгебраическая разность накопленных погрешностей в пределах зубчатого колеса

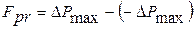
где 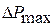, 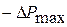- наибольшая соответственно положительная и отрицательная погрешность.

График накопленной погрешности шага изображен на рис. 1.70.

Рис. 1.70

3. Радиальное битье зубчатого венца 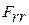— это разность действительных предельных положений контуру в пределах зубчатого колеса /рис. 1.71/:

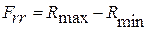/1.75/

где 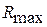, 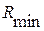- соответственно больше всего и наименьшее предельное положение контуру зуба.

4. Колебание длины общей нормали 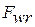, - это разность между предельными длинами общей нормали /рис. 1.72/:

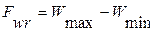/1.75/

где 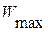, 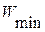- больше всего и наименьшее значение длины общей нормали.

На параметры кинематической точности установлены допуски.

Рис. 1.71

Рис. 1.72

Допуски 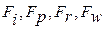наведены в таблицах.

Нормы плавности работы характеризуют параметры, погрешности которых|каких| на один оборот зубчатого колеса составляют|складывают,сдают| часть кинематической погрешности.

1. Наибольшая местная кинематическая погрешность зубчатого колеса 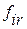- это удвоенная амплитуда составной кинематической погрешности /наибольшая разность между соседними предельными значениями погрешностей зубчатого колеса, черт. 1.73/.

2. Погрешность профиля зуба 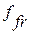— это расстояние между соприкасающимся к|до| реальному профилю номинального профиля. Погрешность профиля уменьшает поверхность контакта зубов и ухудшает плавность работы /рис. 1.74/.

3. Погрешность шага 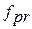— это разность между действительным и номинальным шагами /рис. 1.75/:

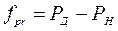
Рис. 1.73

Рис. 1.74 Рис. 1.75

На все параметры норм плавности предусмотренные допуски.

Допуски 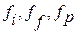и тому подобное наведенные в таблицах.

Нормы контакта зубов.

Контакт зубов в передаче определял долговечность. Качества контакта могут характеризоваться пятном контакта, погрешностью направления зуба, не параллельностью осей и их перекосом.

1. Суммарная прямая контакта - это часть активной боковой поверхности зуба колеса, на которой|какой| размещаются следы прилегания его к|до| зубам парного|четного| колеса. На зубы парного|четного| колеса предварительно наносят краску. Пятно контакта определяется относительными размерами - в процентах /рис. 1.76/.

Рис. 1.76

2. Погрешности направления зуба - расстояние за нормами между двумя более близкими номинальными делительными линиями зуба, между которыми|какими| размещенная действительная делительная линия зуба /рис. 1.77/.

Рис. 1.77

3. Отклонением от параллельности осей 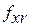называется отклонение от параллельности проекций рабочих осей зубчатых колес в передаче на плоскость, в которой|какой| лежит одна из осей и точки второй оси в средней плоскости передачи /рис. 1.78,а/.

Средняя площадь - это площадь, что проходит через средину рабочей ширины венца:

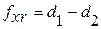. /1.77/

Рис. 1.78

4. Перекос осей - отклонение от параллельности проекций рабочих осей зубчатых колес в передаче на плоскость, параллельную одной из осей и перпендикулярную к|до| плоскости, в которой|какой| лежит эта ось, и точка пересечения второй оси.

Средняя плоскость передач /рис. 1.78, 6/

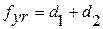. /1.78/

Виды сопряжений зубов колес.

С целью предотвращения заклинивания при перегреве передач, обеспечению условий смазки и ограничению мертвого хода при реверсировании в передаче должен быть боковой зазор 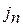/между нерабочими профилями зубов сопрягаемых| колёс/. Предусмотрено шесть видов сопряжений, которые|какие| определяют разные|различные| значения 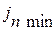/рис. 1.79/. Каждый вид сопряжения имеет условное название, символ и предусматривает различные значения зазора, а именно: вид А - увеличенный; В - нормальный; С - уменьшенный; D - малый; Е - особенно|в особенности| малый; Н - нулевой

/рис. 1.80/.

В результате увеличения температуры при работе в передаче размеры колес увеличиваются, а боковой зазор уменьшается. Необходим для компенсации температурных деформаций и размещения смазочного материала боковой зазор

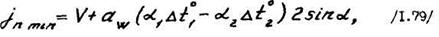
где V - толщина слоя смазки между зубами; 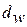- межосевое расстояние;

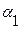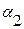, - температурные коэффициенты линейного расширения материала соответственно колес и корпуса|;

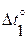
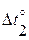- отклонение температур колес и корпуса| от 20 °С;

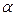— угол профиля выходного контура.

Рис. 1.79

Рис. 1.80

На боковой зазор установлен допуск 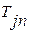, который|какой| определяется разностью между наибольшим и наименьшим зазорами.

На него установлено восемь видов допуска 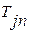: x, в, z, а, b, c, d, h.

Принципы построения системы допусков для зубчатых конических передач по ГОСТ 1758-81 /СT СЭВ 186-75, СТ| СЭВ 1161-78/ аналогичны принципам построений системы для цилиндровых передач.

Обозначение параметров точности.

Примеры|приклады| обозначения зубчатых колес и передач:

7-в ГОСТ 1643-87- цилиндровая передача 7-ой степени точности с видом сопряжения В, видом допуска бокового зазору b;

8-7-6-Bа ГОСТ 1643-88- цилиндрическая зубчатая передача 8-ой степени точности по нормам кинематической точности, 7-го - по нормам плавности, 6-го - по нормам контакта зубов, с видом сопряжения B, видом допуска бокового зазору а.

ЛЕКЦИЯ 18.

Размерные цепи: их классификация, основные термины и определения. Методы решения размерных цепей

Для нормальной работы машин необходимо, чтобы составляющие их детали и их поверхности занимали одна относительно другой определённое, соответствующее её служебному назначению положение.

При расчёте точности относительного положения деталей и их поверхностей учитывают взаимосвязь многих размеров.

Например,

А₁

А₀

А₁

А₂ А₀

А₂

Эту взаимосвязь устанавливаю с помощью размерных цепей.

Размерной цепью называется совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи.

Замкнутость размерного контура – необходимое условие для составления и анализа размерной цепи.

Однако на рабочем чертеже размеры следует проставлять в виде не замкнутой цепи - не проставляют размер замыкающего звена, т.к. для обработки он не требуется.

Размеры, образующие размерную цепь, называют звеньями размерной цепи.

По взаимному расположению звеньев размерные цепи делят на линейные, плоские и пространственные.

Размерную цепь называю линейной, если все ей звенья номинально параллельны одно другому и, следовательно, могут проектироваться без изменения их величины на две или несколько параллельных линий.

Размерная цепь называется плоской, если все звенья её лежат в одной или нескольких параллельных плоскостях.

Пространственной называют размерную цепь, все или часть звеньев которой расположены в непараллельных плоскостях.

Размерные цепи, звеньями которых являются угловые размеры, называются угловыми размерными цепями.

При анализе точности электрических и электронных элементов машин и приборов используют цепи, звеньями которых являются величины сопротивлений, ёмкости, индуктивности, тока, напряжений, и других электрических и физических параметров.

Задача обеспечения точности при конструировании изделий решается с помощью конструкторских размерных цепей, а при изготовлении деталей – с помощью технологических размерных цепей, выражающих связь размеров обрабатываемой детали по мере выполнения технологического процесса.

Когда решается задача измерения величин, характеризующих точность изделия, используют измерительные размерные цепи, элементами которой являются размеры детали и измерительного средства.

Звенья размерной цепи делят на составляющие и одно замыкающее.

Замыкающим называется размер А₀, который получается последним в процессе обработки детали, сборки узла машины или измерения.

Его величина и точность зависит от величины и точности всех остальных размеров цепи, называемых составляющими, которые обозначают А₁, А₂ … А_m-1, где m – общее количество звеньев размерной цепи.

Звено сборочной размерной цепи, которое определяет функционирование механизма и для обеспечения, точности которого решается размерная цепь, называется исходным размером.

Это может быть зазор , натяг, или перемещение какой-либо детали.

Исходя из предельных значений исходного размера рассчитывают допуски и отклонения всех остальных размеров цепи.

В процессе сборки исходный размер, как правило, становится замыкающим.

Различают увеличивающие и уменьшающие размеры размерной цепи.

Увеличивающим называют размер, с увеличением которого, величина замыкающего размера также увеличивается.

Уменьшающим называется размер, с увеличением которого, величина замыкающего размера уменьшается.

В приведенном размере размер А₁ увеличивающий, а А₂ – уменьшающий.

На схемах размерных цепей увеличивающие и уменьшающие звенья условно обозначают стрелкой над буквой. На увеличивающих звеньях стрелку ставят вправо, на уменьшающих – влево.

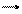Например: А₁

А₂ А₀

При размерном анализе могут встречаться взаимосвязанные размерные цепи с общими звеньями, а также цепи, в которых исходным звеном является одно из составляющих звеньев основной цепи. В последнем случае цепи называют производными.

Расчёт и анализ размерных цепей позволяет:

- установить количественную связь между размерами деталей машины и уточнить номинальные значения и допуски взаимосвязанных размеров исходя из эксплуатационных требований и экономической точности обработки детали и сборки машины;

- определить, какой вид взаимозаменяемости (полный или ограниченный) будет наиболее рентабельный;

- добиться наиболее правильной простановки размеров на рабочих чертежах;

- определить операционные допуски и пересчитать конструктивные размеры на технологические (в случае несовпадения конструктивных баз с технологическими).

Расчёт размерных цепей и их анализ – обязательный этап конструирования машин, способствующий повышению качества, обеспечению взаимозаменяемости и снижению трудоёмкости их изготовления.

Сущность расчёта размерной цепи заключается в установлении допусков и предельных отклонений всех её звеньев исходя из требований конструкции и технологии. При этом различают две задачи:

1. Определение допуска и предельных отклонений составляющих размеров по заданным номинальным размерам всех размеров цепи и допуску исходного размера.

Такая задача возникает при проектировочном расчёте и называют её условно прямой задачей.

2. Определение номинального размера и допуска (предельных отклонений) замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев (такая задача возникает при необходимости выполнить проверочный расчёт на соответствие допуска замыкающего звена допускам составляющих звеньев).

Такую задачу условно называют обратной задачей.

Обе задачи можно решать различными методами, которые обеспечивают полную или неполную (ограниченную) взаимозаменяемость.

На практике применяется два основных метода: метод максимума и минимума, и теоретико-вероятностный метод.

При использовании метода максимума и минимума допуск замыкающего звена определяется арифметическим сложением допусков составляющих звеньев, т.е. предполагается, что величины составляющих звеньев в пределах их допусков могут принимать любые значения, в том числе и предельные.

Метод максимума и минимума обеспечивает полную взаимозаменяемость. Заданная точность сборки достигается без какой-либо пригонки или сортировки деталей

Теоретико-вероятностный метод основан на следующем.

На практике в условиях серийного и массового производства размеры деталей распределяются по закону, близкому к закону нормального распределения, (который мы изучали на предыдущей лекции).

В соответствии с этим законом большая часть деталей имеет отклонения близкие к середине поля допуска.

Вероятность появления деталей с размерами, близкими к предельным, – т.е. на краях поля допуска – ничтожно мала.

6σ

dmin

dmax

А практике принимают, что границы вероятного рассеяния размеров деталей 6σ (±3σ) совпадают с границами полей допусков. При этом допускается ничтожно малая вероятность несоблюдения предельных значений замыкающего звена 0,0027 или 0,27%

Это допущение позволяет значительно расширить допуски составляющих размеров и тем самым снизить себестоимость деталей. При этом заранее допускается, что 0,27% деталей попадут в брак.

ЛЕКЦИЯ 14.

Расчёт размерных цепей методом максимума и минимума. Основные зависимости. Пример решения.

В предыдущей лекции мы рассмотрели основные идеи метода максимума и отметили, что в соответствии с данным методом величины составляющих звеньев в пределах их допусков могут принимать любые значения, в том числе и предельные.

Метод максимума и минимума обеспечивает полную взаимозаменяемость.

Рассмотрим основные соотношения метода максимума и минимума при решении обратной задачи.

Пусть размерная цепь содержит m – звеньев из которых n – увеличивающих звеньев и р – уменьшающих.

Номинальный размер замыкающего звена линейной размерной цепи определяется формулой

.

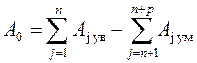Допуск замыкающего звена равен сумме допусков составляющих звеньев

.

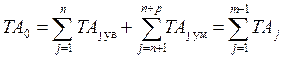Наибольшее и наименьшее предельные отклонения замыкающего звена определяются по формулам:

;

.

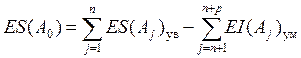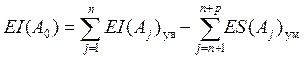Координата середины поля допуска замыкающего звена определяется по формуле

.

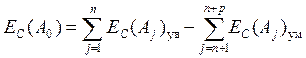Предельные отклонения замыкающего звена связаны с координатой середины поля допуска замыкающего звена соотношениями

ТA0

ES(A0)

0 0

EI(A0)

EС(A0)

;

.

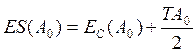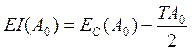На основе приведенных формул можно сделать некоторые выводы:

1. Чем больше количество составляющих звеньев, тем больше допуск замыкающего звена.

2. Чем больше допуски составляющих звеньев, тем больше допуск замыкающего звена.

3. Чтобы обеспечить наименьшую погрешность замыкающего звена нужно соблюдать принцип кратчайшей цепи с возможно меньшим числом звеньев.

4. Порядок обработки и сборки деталей надо строить так, чтобы замыкающим был менее ответственный размер, т.к. его погрешность будет наибольшей.

Рассмотрим пример.

А₁ А₂

А₃ А₅

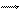А₁ А₂

А₀

А₃ А₄ А₅

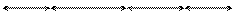
А₄ А₀

А₁ = 101^+0,14; А₂ = 50^+0,1; А₃ = А₅ = 5_-0,03; А₄ = 140_-0,1.

Величина замыкающего звена (номинальный размер) равна

А₀ = (101+50) – (5+140+50) = 1 мм.

Допуски составляющих звеньев

ТА_j = ЕS(А_j) – ЕI(А_j);

ТА₁ = 0,14 – 0 = 0,14; ТА₂ = 0,1 – 0 = 0,1;

ТА₃ = ТА₅ = 0 – (-0,03) = 0,03; ТА₄ = 0–(-0,1)=0,1.

Допуск замыкающего звена

ТА₀ = 0,14+0,1+0,03+0,03+0,1 = 0,4 мм.

Предельные отклонения замыкающего звена

ЕS(А₀) = 0,14+0,1 – (-0,03) – (-0,03) – (-0,1) = 0,4 мм.

ЕI(А₀) = 0 + 0 – 0 – 0 – 0 = 0.

А₀ = 1^+0,4; ТА₀ = 0,4 – 0 = 0,4 мм.

Как видно из результатов расчёта, допуск замыкающего звена получился наибольший по сравнению с допусками составляющих звеньев.

Предельные размеры замыкающего звена:

А_{0 max} = А₀ + ES(A₀) = 1 + 0,4 = 1,4 мм;

А_{0 min} = А₀ + EI(A₀) = 1 + 0= 1 мм.

Решение прямой задачи по методу максимума и минимума.

Прямая задача в конструкторской практике встречается наиболее часто. Основная цель при этом – назначить допуски на составляющие звенья так, чтобы обеспечить заданную точность исходного размера.

Прямая задача по методу max и min решается двумя способами:

- способ равных допусков;

- способ допусков одного квалитета.

Способ равных допусков применяют, если размеры звеньев, составляющих размерную цепь, являются величинами одного порядка, например, входят в один интервал и могут быть выполнены с примерно одинаковой экономической точностью.

В этом случае можно принять

ТА₁ = ТА₂ = … = ТА_j т.е. ТА₀ = (m – 1) · ТА_j, откуда ,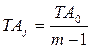

где m – общее количество звеньев размерной цепи, включая и исходное звено.

Полученный средний допуск корректирует в зависимости от величина составляющих размеров так, чтобы соблюдалось правило:

,

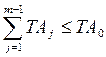т.е. чтобы сумма допусков составляющих звеньев не превышала допуск исходного звена.

Способ равных допусков прост, но имеет ограниченную область применения.

Способ допусков одного квалитета.

При использовании данного способа предполагают, что по известному допуску исходного звена допуски на остальные звенья могут быть назначены по одному квалитету с учётом величин этих звеньев.

Требуемый квалитет определяют следующим образом.

Как вы помните, допуск любого размера в интервале 1…500 мм определяется формулой

Т = а · i.

Т.к. мы приняли, что на составляющие звенья будем назначать допуски по одному квалитету, то количество единиц допуска а будет для всех звеньев одно и тоже.

А единица допуска i будет для каждого размера своя, в зависимости от того, в какой интервал попадёт этот размер.

Как вы помните .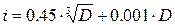

Запишем условие равенства допуска исходного звена сумме допусков остальных звеньев.

ТА₀ = а·i₁ + а·i₂ + … + а·i_j + … + а·i_{m – 1};

т.е. ,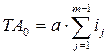

Откуда .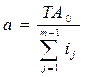

Полученное количество единиц допуска округляем до ближайшего стандартного и по нему в соответствии с СТ СЭВ 145-75 определяем квалитет.

По известному квалитету и номинальным размерам составляющих звеньев определяем их допуски.

Рекомендуется для охватывающих размеров допуски определять как для основного отверстия, а для охватываемых – как для основного вала.

Затем производится проверка на соблюдение условия.

.

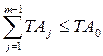Если это условие не соблюдается, на одно из звеньев размерной цепи допуск назначают по более точному квалитету.

Пример. Рассмотрим туже размерную цепь, но для решения прямой задачи методом допусков одного квалитета. Пусть заданы номинальные размеры всех звеньев и допуск исходного звена А₀.

А₁ А₂

А₀

А₃ А₄ А₅

А₁ = 101; А₂ = 50; А₃ = А₅ = 5; А₄ = 140 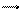; А₀ = 1^+0,75.

Допуск исходного звена

ТА₀ = ES – EI = 0,75 – 0 = 0,75 = 750 мкм.

Определим число единиц допуска

.

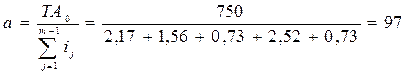По СТ СЭВ 145-75 10^му квалитету соответствует а=64, а 11^му а=100.

Принимаем а = 100, т.е. 11^й квалитет и определяем по таблицам допуски для составляющих звеньев.

ТА₁ = 0,22; ТА₂ = 0,16; ТА₃ = ТА₅ = 0,075; ТА₄ = 0,25 мм.

Проверяем условие равенства допуска исходного звена сумме допусков составляющих звеньев.

0,22 + 0,16 + 0,075 + 0,075 + 0,25 = 0,78 > 0,75,

т.е. условие не соблюдается.

На четвёртое звено назначаем допуск не по 11^му, а по 10^му квалитету ТА₄ = 0,16 мм.

При этом условие соблюдается

0,22 + 0,16 + 0,075 + 0,075 + 0,16 = 0,69 < 0,75.

В соответствии с рекомендациями по полученным допускам назначаем отклонения с учётом того, что размеры А₁ и А₂ – охватывающие, а А₃, А₄, А₅ – охватываемые.

А₁ = 101^+0,22; А₂ = 50^+0,16; А₃ = А₅ = 5_-0,075; А₄ = 140_-0,16.

ЛЕКЦИЯ 15.

Расчёт размерных цепей теоретико-вероятностным методом. Метод групповой взаимозаменяемости. Селективная сборка. Методы регулирования и пригонки.

На предыдущих лекциях мы изучили закон нормального распределения вероятностей и рассмотрели сущность теоретико-вероятностного метода расчёта размерных цепей.

Решение обратной задачи теоретико-вероятностным методом.

Полагая, что погрешности составляющих и замыкающего размеров подчиняются закону нормального распределения, а границы их вероятного рассеяния (6σ) совпадают с границами полей допусков, можно принять

; .

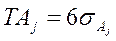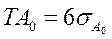При этом 0,27% деталей окажутся бракованными.

На основе методов теории вероятностей можно получить выражение для допуска замыкающего звена.

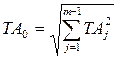- геометрическая сумма.

После распределения допуска замыкающего звена определяют координату середины поля допуска

.

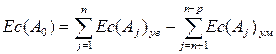Затем определяют предельные отклонения замыкающего звена

;

.

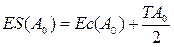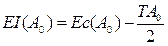Пример:

А₁ = 40_-0,039; А₂ = 60^+0,046.

А2

А1

А0

Определим допуски составляющих звеньев

ТА₁ = 0 – (-0,039) = 0,039 = 39 мкм.

ТА₂ = 0,046 – 0 = 0,046 = 46 мкм.

Определим допуск замыкающего звена

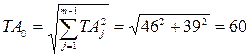мкм.

По м