Синтез механізмів за заданими положеннями ланок

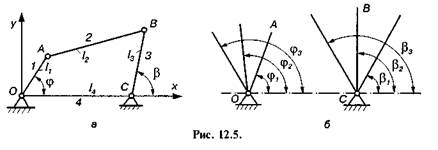
Розглянемо задачу про синтез шарнірного чотириланкового механізму (рис. 12.5, а) за заданими положеннями його ланок.

Для спрощення задачі слід припустити, що нерухомі шарніри О і С розташовані на осі Ох, від якої ведеться відлік кутів ц і в, і прийняти, що кут б = 0, то при заданих довжинах ланок будь-якому заданому значенню ц, кута ц (рис. 12.5, б) відповідатиме цілком визначене значення в, кута в, а тому кількість параметрів механізму, які необхідно визначити, дорівнюватиме трьом (див. параграф 12.3). Це параметри л₂ =

Отже, 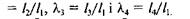якщо будуть задані три положення ланки ОА (рис.

12.5, б) кутами ц_[; ц₂, ц₃, а три відповідні їм положення ланки
ВС — кутами в,, в₂, в₃, то завжди будуть визначені параметри
л₂, л₃, л₄, оскільки кількість рівнянь вигляду (12.8) дорівнює
кількості цих параметрів.

Поставлену задачу можна розв'язати аналітичним і графічним методами.

Аналітичний метод. Зобразимо сторони механізму (рис. 12.6) у вигляді векторів л,, л₂, л₃, л₄, причому л] = 1. Тоді маємо

л, + л₂ = л₄ + л₃. (12.9)

Проектуємо обидві частини рівнянь (12.9) на осях Ох, Оу. Позначимо кут, утворений шатуном АВ з віссю Ох, буквою д і отримаємо для довільного /-го положення механізму рівняння проекцій на осях Ох і Оу у вигляді

або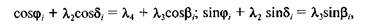

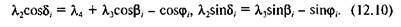
Підносимо почленно рівняння (12.10) до квадрата і додаємо їх. Тоді отримаємо

Перенесемо 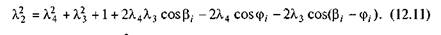л\ у праву частину (12.11) і поділимо всі члени на 2л₄. Розв'язуючи рівняння відносно cos ц,, матимемо

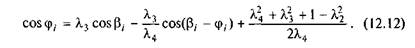
Введемо позначення:

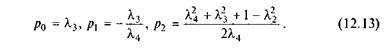
Тоді (12.12) запишеться так:

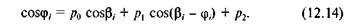
Підставляючи у рівність (12.14) задані кути ц,, ц₂, ц₃ і в,, в₂, в₃ (див. рис. 12.5, б), записуємо систему, складену із трьох лінійних рівнянь:

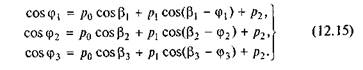
Розв'язуючи сумісно цю систему рівнянь, визначаємо величини коефіцієнтів р₀, />!, р₂, після чого за допомогою співвідношень (12.13) можна знайти невідомі параметри л₂, л, і л₄.

Якщо необхідно спроектувати механізм за двома положеннями ланок ОА і ВС, то один із параметрів механізму можна задати довільно і задача матиме нескінченну кількість можливих розв'язків.

Такі задачі можна розв'язати графічним методом за допомогою нескладних геометричних побудов.

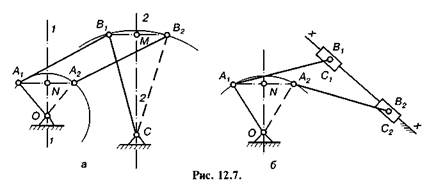
Синтез механізмів за двома заданими положеннями шатуна.Нехай задано два положення /Й,в, і А₂В₂ шатуна шарнірного чо-тириланкового механізму (рис. 12.7). Необхідно знайти положення точок О і С — центрів обертання ланок механізму, які входять у кінематичні пари зі стояком. Точки А\ і А₂ повинні лежати на колі з центром у точці О, а точки B_t і В₂ — на колі з центром С. Оскільки через дві точки можна провести нескінченну кількість кіл, то геометричним місцем цих кіл є прямі 11 або 22, які перпендикулярні до хорд A_tA₂ або В_{В₂ і проходять через їх середину N або М. Точку О можна розмістити у будь-якій точці прямої 7/, а точку С — прямої 22. Отже, для 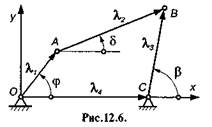вказаного завдання можна побудувати нескінченну кількість механізмів, які задо вольняють задані умови. Додаткові умови можна накласти, якщо, наприклад, поставити умову, щоб механізм був двокривошипним або кривошипно-коромисловим тощо.

Якщо вимагається, щоб одна із точок ланки АВ, наприклад точка В, рухалась вздовж нерухомої прямої хх, то центр С кола повинен знаходитися у нескінченності, обертова пара С перетворюється у поступальну (рис. 12.7, б), тоді отримаємо кривошипно-повзунковий механізм.

Можна поставити додаткову вимогу, щоб при заданому переміщенні шатуна АВ кути повороту ц і в відповідно ланок ОА і ДС були також заданими (рис. 12.8). Тоді з'єднуємо точки А\ і А₂ прямою і відкладаємо при точках А_{ і А₂ кути, що дорівнюють 90° - ц/2. Точка перетину О прямих Б_гб\ і А₂а₂ визначить положення осі О обертання ланки ОА. Так само, якщо з'єднати точки В\ і В₂ і при цих точках відкласти кути 90° - в/2, то точка С перетину прямих B_tb_{ і В₂Ь₂ визначить положення осі обертання С ланки ВС.

Синтез механізмів за трьома положеннями шатуна(рис. 12.9). Задача зводиться до знаходження центра кола, яке проходить через три точки. Як відомо, ця задача має тільки один розв'язок. Отже, маючи три точки А\, Б₂, А₃, з'єднуємо прямими