Умова існування кривошипа в чотириланкових механізмах

123 4

До найпростіших механізмів, які широко використовуються у техніці, належать шарнірні чотириланкові механізми. Основна характеристика таких механізмів — прокручування їх ланок (наявність у них одного або двох кривошипів), яке залежить від співвідношення довжин ланок. Для встановлення цієї умови розглянемо шарнірний чотириланковий механізм (рис. 12.1), в якого довжини ланок відповідно становлять 1_ОА = а, 1_АВ = в,l_bc=c,l_DC=d

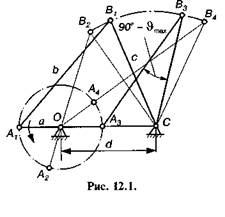Для того щоб ланка ОА могла стати кривошипом, вона повинна при обертанні послідовно пройти через крайнє ліве ОА_{ і праве ОА_гположення. Тоді, прийнявши, що а — довжина найкоротшої ланки, d — найдовшої, та використавши відомі співвідношення між довжинами сторін трикутника (довжина сторони трикутника менша суми довжин двох інших сторін), записуємо такі нерівності:

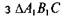
a + d<b + c (12.1)

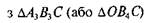
d-a<b + c. (12.2)

Незалежно від співвідношення довжин b і с нерівність (12.1) завжди забезпечує виконання нерівності (12.2). Якщо ж найдовшою ланкою буде ланка АВ або ВС (Ь > с > d або с > b > d), то нерівність (12.1) тільки підсилюється.

Нерівність (12.1) дає змогу дати загальне формулювання умови прокручування ланок шарнірного чотириланкового механізму, тобто існування кривошипа, а саме — найкоротша ланка шарнірного чотириланкового механізму може бути кривошипом, якщо сума довжин найкоротшої і найдовшої ланок менша суми довжин решти ланок. Це положення носить назву правила Грасгофа.

Використовуючи це правило, шарнірні чотириланкові механізми поділяють на три групи:

• механізм буде кривошипно-коромисловим (див. рис. 12.1),
якщо розміри його ланок задовольняють правило Грасгофа
(12.1) і за стояк прийнято ланку b або d, розташовану біля найкоротшої ланки а;

• механізм буде двокривошипним, якщо його розміри
відповідають правилу Грасгофа і за стояк прийнято найкоротшу
ланку а (рис. 12.2, а). Це випливає з того, що якщо кривошип
при виконанні правила Грасгофа виконує повний оборот
відносно стояка ОС і шатуна АВ (див. рис. 12.1), то й ці ланки
здійснюють повний оборот відносно стояка;

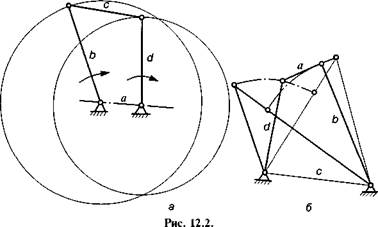
•механізм буде двокоро-мисловим, якщо його розміри не задовольняють правило Грасгофа, а також у випадку, коли задовольняють це правило, але найкоротша ланка є шатуном (рис. 12.2, б). Тому можливість цієї ланки бути кривошипом зникає, оскільки вона не є ланкою, розташованою біля стояка.

У граничному випадку, коли нерівність (12.1) перетворюється у рівність, усі ланки механізму в одному з крайніх положень розташовано вздовж однієї прямої. Внаслідок цього з'явиться невизначеність руху відповідної ланки (вона може рухатися або в одному, або в іншому напрямку).

У кривошипно-повзунковому механізмі (рис. 12.3, а) ланка 1 буде кривошипом, якщо при обертанні вона пройде положення ц = 90° і 270°, що можливо, коли виконується умова

де г — довжина ланки ОА; 1 — ланки АВ; е — зміщення (дезаксіал).

Штриховою лінією зображена схема механізму, коли е < 0. Якщо г > І - е , то ланка 1 буде коромислом, і такий механізм правильніше називати коромислово-повзунним.

У кулісному механізмі (рис. 12.3, б) ланка / може бути кривошипом; ланка 3 (куліса) буде кривошипом, якщо при обертанні пройде положення ц = 270°, що можливо при виконанні умови

г>а + е, (12.4)

де г — довжина кривошипа ОА\ а = І_ос — міжосьова відстань; е — зміщення куліси; е = І_вс. У цьому випадку маємо механізм з обертовою кулісою. Якщо г < а + е, то куліса 3 буде коромислом (механізм з коливальною кулісою). Найбільш розповсюджені кулісні механізми, в яких зміщення е = 0.