Тертя гнучкої ланки

1 23

У техніці широко застосовуються механізми з гнучкими ланками (пасові та канатні передачі, стрічкові гальма та транспортери тощо). У таких механізмах передача руху можлива лише при наявності достатньої сили тертя між гнучкою ланкою і шківом.

Формулу, що зв'язує основні параметри передачі гнучкою ниткою, вивів у 1765 р. Л. Ейлер [1, 4].

Для виведення цієї формули розглянемо ковзання гнучкої нитки по нерухомому шківу (рис. 6.19, а). Тоді кінець гнучкої нитки, який при своєму русі набігатиме на шків, назвемо побіжним кінцем, а той кінець, який збігатиме зі шківа, —збіжним. Дуга аЬ, по довжині якої нитка прилягає до шківа, називається дугою обхвату, а центральний кут а, що їй відповідає, — кутом обхвату. Нехай натяг набіжного кінця буде /J, а збіжного Р₂. Знайдемо зв'язок між цими натягами. При цьому зробимо такі спрощення. Вважатимемо, що нитка не розтягується і не чинить опору згину при набіганні і збіганні нитки. Далі припустимо, що нитка рухається зі сталою швидкістю н. Масою нитки та її відцентровими силами інерції знехтуємо.

Щоб надати гнучкій ланці рівномірного руху в бік сили F₂, необхідно подолати не тільки опір сили /є, але й силу тертя F_fміж ниткою і шківом, тобто

звідки

Отже, при 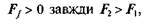а це значить, що при пере-

ході від точки а до точки Ь, де нитка набігає і збігає зі шківа, сила тертя постійно збільшується від fi до F₂. Для встановлення залежності між цими величинами виділимо на дузі обхвату

нескінченно малий елемент нитки 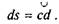Якщо на початку

цього елемента — в точці с — натяг має деяке значення F, то в

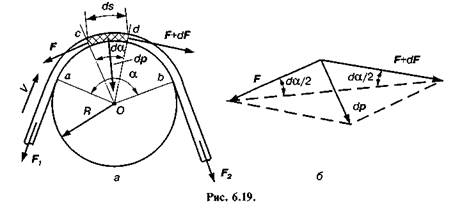
кінці його, як вказано раніше, він збільшується на df і дорівнюватиме F+ dF. Нерівномірність натягу зумовлюється наявністю сил тертя між елементом нитки і шківом. Лінії дії сил F і F + dF будуть дотичними до шківа і перпендикулярними до радіусів, проведених з точки О в точки дотику с і d.

Елементарна сила тертя dF_f згідно з рівнянням (6.48) має вигляд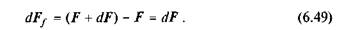

Згідно з формулою Амонтона—Кулона, сила тертя визначається за формулою

де dp — елементарна сила тиску елемента ds на шків; /— коефіцієнт тертя.

Із співвідношення (6.49) і (6.50) випливає

Позначивши через da. кут, який стягується дугою cd, знаходимо суму проекцій сил, прикладених до елемента cd, на радіус, проведений через середину дуги cd. У результаті дістанемо

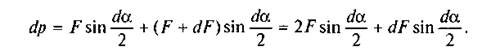
Нехтуючи нескінченно малими величинами другого порядку 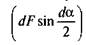і враховуючи, що для малих кутів 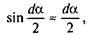одер-

жуємо

dp = Fda. (6.52)

Підставивши знайдене значення для сили dp в рівняння (6.51), дістанемо

звідки, розділивши змінні, запишемо

Інтегруючи ліву і праву частини цього рівняння, дістаємо

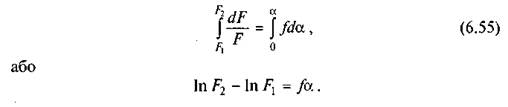
Потенціюючи цей вираз, одержуємо відому формулу Ейлера,

з якої випливає, що сила натягу зростає із зростанням кута обхвату α і коефіцієнта тертя f/ Легко побачити, що при сталому коефіцієнті тертя збільшення кута обхвату дає дуже швидке зростання сили F₂.

Підставивши в рівняння (6.48) значення F₂ (6.56), дістанемо для сили тертя вираз

Сила F_f є тією найбільшою коловою силою, яку можна передати шківу. Якщо коловий опір на веденому шківі дорівнює або менший від сили F_f, то гнучка нитка змусить шків обертатися. Коли ж коловий опір більший від сили Ff, то гнучка ланка ковзатиме по шківу, не обертаючи його. Таким чином, натягнена силами F₁ і F₂ гнучка ланка при F₂ > F₁ може передавати веденому шківу обертовий момент

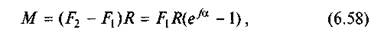
де R — радіус шківа.

Формула Ейлера дає тільки наближений зв'язок між натягами гілок гнучкої ланки. Тому останнім часом у технічній літературі рекомендуються також і інші методи розрахунку, які тут не наводяться.

Тертя кочення

Як уже зазначалося, тертям кочення називають опір, який виникає при перекочуванні одного тіла по поверхні іншого.

Цей опір виникає головним чином від того, що тіла не абсолютно тверді і завжди дещо деформуються в місцях їх стикання. Досвід показує, що опір перекочуванню тіл залежить від пружних властивостей тіл, які стикаються, їх кривизни та сили притискання.

Фізичні явища, які викликають тертя кочення, так само, як і при терті ковзання, вивчені мало. В технічних розрахунках користуються переважно даними, одержаними при експериментальних дослідженнях, які проводились над різними конкретними об'єктами: котками, колесами, роликами і шариками в підшипниках кочення тощо.

На перемагання опору під час перекочування тіл витрачається якась робота, яка йде переважно на деформацію стичних поверхонь. Якщо на коток /, який лежить на горизонтальній площині 2 (рис. 6.21, а), діє тільки сила Q, то деформація котка і опорної поверхні симетричні відносно лінії дії Q. В результаті деформації коток і опорна поверхня дотикаються не в одній точці (лінії), а деякою площиною контакту, ширина якої АВ. Реакція з боку опорної поверхні розподіляється по всій площині контакту. Згідно з положенням теорії пружності напруження в зоні контакту розподіляються за еліптичним законом. При цьому крива напружень симетрична, а значить, напрямок рівнодіючої N цих напружень збігається з напрямком сили Q. За модулем нормальна реакція N дорівнює силі Q і напрямлена в протилежний від неї бік.

Якщо на коток діє на деякій висоті h ще й горизонтальна сила F (рис. 6.21, б), то деформація котка і опорної поверхні вже несиметричні відносно лінії дії сили Q. Це пояснюється тим, що ділянка ВС буде знаходитися в зоні зростання деформації, а ділянка АС — у зоні спадання деформації (ВС > АС). Завдяки внутрішньому тертю в матеріалі тіл, що деформуються, криві навантаження і розвантаження матеріалу не збігаються (явище пружної післядії і гістерезису). Тому крива напружень у зоні СВ буде вища від кривої в зоні AC, a значить, розподіл напружень відносно лінії дії сили Q буде несиметричним з максимумом, зсунутим у бік руху котка. Отже, рівнодіюча N напружень буде зміщена в бік руху від точки С на величину k, яка називається плечем сили, або коефіцієнтом тертя кочення.

Враховуючи, що деформація тіл при коченні незначна порівняно з розмірами тертьових тіл, приймаємо, що CD = h. Тоді, записуючи рівняння моментів сил, що діють на коток, відносно точки С, маємо

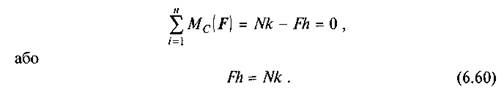
Величина М_к = Nk називається моментом тертя кочення, а Fh — обертальним (рушійним) моментом. Якщо врахувати, що N = Q, то момент тертя кочення матиме вигляд

де роль коефіцієнта пропорційності відіграє плече тертя k. Як видно з рис. 6.21 і формули (6.61), коефіцієнт тертя кочення k вимірюється одиницею довжини (мм або см), в той час коефіцієнт тертя ковзання є безрозмірна величина, і визначає максимальне значення зміщення нормальної реакції N відносно лінії дії сили Q.

Коефіцієнт тертя кочення залежить від пружних властивостей матеріалів тертьових тіл, стану їх поверхні та радіусів кривизни. На практиці, як правило, користуються значеннями, знайденими експериментальним шляхом. Наприклад, для стального колеса і рейки k ~ 0,05 мм, для гартованих стальних шариків і роликів — 0,01 мм, чавуну по чавуну — 0,05 мм, дерева по сталі — 0,3—0,4 мм, дерева по дереву — 0,5—0,8 мм.

З рівнянь (6.60) і (6.61) знаходимо силу F, яку необхідно прикласти до котка, щоб він рівномірно перекочувався по площині:

На практиці інколи користуються умовною безрозмірною величиною

яка називається зведеним (умовним) коефіцієнтом тертя кочення. Тоді залежність (6.62) набуває такого ж вигляду, як і при терті ковзання:

Втрати енергії при терті кочення, як правило, значно менші, ніж при терті ковзання. Ось чому в техніці намагаються якомога більше замінити тертя ковзання тертям кочення. Для цього широко використовується колісний транспорт, підшипники кочення, шарикові або роликові напрямні тощо.

Оскільки на практиці, звичайно, тертя кочення супроводжується тертям ковзання, то важливо розглянути, за яких умов яке тертя має місце. Тут можливі три випадки.

1. Якщо 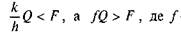— коефіцієнт тертя ковзання, то коток буде тільки котитися. Об'єднавши ці нерівності,
одержимо умову чистого кочення:

Отже, при чистому коченні необхідно, щоб зведений коефіцієнт тертя кочення (k/h) був меншим від коефіцієнта тертя ковзання.

2. Якщо ж 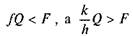, то циліндр буде тільки ков
зати. Тоді умова чистого ковзання зображується так:

При чистому ковзанні необхідно, щоб коефіцієнт тертя ковзання був меншим за зведений коефіцієнт тертя кочення.

3. Якщо ж 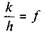, то можливе спільне кочення і ковзання,

тобто з'являється невизначеність у русі.

Розглянемо деякі приклади з техніки, де використовується тертя кочення.

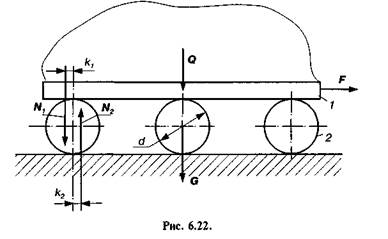
Переміщення тіл на котках.Для переміщення важких тіл (машин, верстатів, споруд тощо) на невеликі відстані часто використовують котки у вигляді циліндричних стержнів чи труб, на які спираються ці тіла або платформа з вантажем, як це зображено на рис. 6.22.

Визначимо силу F, яку необхідно прикласти до платформи 1 для рівномірного переміщення її з вантажем у горизонтальному напрямку. Позначимо через Q вагу платформи і вантажу, G — сумарну вагу котків 2, k_{ і k₂ — коефіцієнти тертя кочення відповідно по платформі і площині (настилу). Якщо умовно прикласти всі сили до одного котка і скласти рівняння рівноваги сил, то дістанемо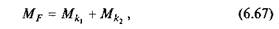

де М_F = Fd — рушійний момент від сили 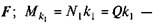момент тертя кочення між котком і платформою (N_l = Q);

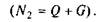
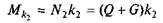— момент тертя між котком і площиною

Підставивши значення моментів у рівняння (6.67), одержимо

Оскільки вага котків порівняно з вагою вантажу, звичайно, мала, то нею можна знехтувати. У такому випадку

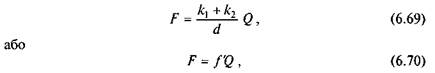
де 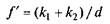— зведений (умовний) коефіцієнт тертя кочення при переміщенні вантажу на котках.

Переміщення вантажів на колесах.Для переміщення вантажів на значні відстані користуються платформами або візками, які обладнані колесами (рис. 6.23), що служать для них рухомими опорами (автомобілі, вагони та інший колісний транспорт). У цьому випадку при переміщенні вантажу з платформою треба перемогти не тільки сили тертя кочення між колесами і опорною поверхнею (дорогою), але і сили тертя ковзання в буксових вузлах, тобто між шипами і підшипниками, через які навантаження передається від платформи до коліс.

Розглянемо випадок рівномірного руху навантаженого візка з однаковими колесами (рис. 6.23). Для знаходження сили F, що забезпечує цей рух, знову умовно прикладемо всі сили і моменти сил до одного колеса та складемо рівняння його руху за один оберт (рівняння робіт):

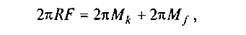
де 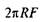— робота сили F; 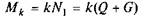— момент тертя кочення; 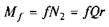— момент сил тертя ковзання в буксі.

Підставивши значення моментів, після відповідних перетворень дістанемо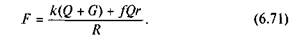

Якщо знехтувати вагою коліс, то залежність (6.71) набуває вигляду

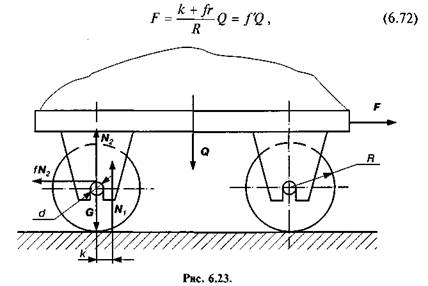
де 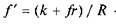— зведений (умовний) коефіцієнт тертя при

переміщенні тіл на колесах.

Якщо замість підшипників ковзання використовуються підшипники кочення, то коефіцієнт тертя /' визначається з

урахуванням зведеного коефіцієнта тертя кочення [46]: для роликових підшипників кочення

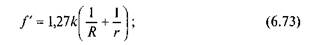
для шарикових підшипників кочення

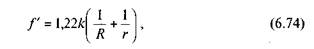
де k — коефіцієнт тертя кочення для гартованих стальних шариків і роликів; R — зовнішній радіус внутрішнього кільця підшипника; г — радіус ролика або шарика.

1 23

Дата добавления: 2016-06-15; просмотров: 2879;