Тертя в обертових кінематичних парах

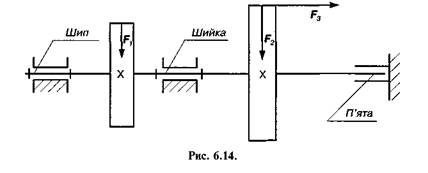
Обертові пари одержали надзвичайно широке поширення в машинах. Найхарактернішим прикладом такої пари може служити пара, утворена цапфою вала або осі та їх опорами. Цапфою називається та частина вала або осі, якою вони спираються на опори. Якщо цапфа передає на опори радіальні сили та розміщена на кінці вала, то її називають шипом (рис. 6.14), а якщо всередині вала, — шийкою. Опори в таких випадках називаються підшипниками. Якщо цапфа передає силу в осьовому напрямку, то її називають п'ятою, а опори — підп 'ятниками.

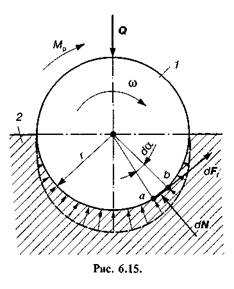
Тертя цапф у підшипниках. При виводі розрахункових формул у такій кінематичній парі використовують, як правило, дві гіпотези. Згідно з першою гіпотезою вважають, що питомий тиск с розподіляється рівномірно на проекції поверхні цапфи на горизонтальну площину (рис. 6.15), тобто

де / — довжина цапфи; d = 1г — її діаметр.

Для забезпечення рівномірного обертання вала 7, який притискається до підшипника 2 силою Q, необхідно прикласти рушійний момент Л/р, що дорівнює моменту тертя, який виникає між ланками 7 і 2.

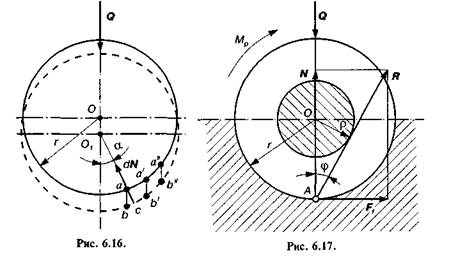
Для визначення цього моменту розглянемо елементарну ділянку ds = ab поверхні цапфи, на яку діє нормальний тиск

де 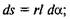/ — довжина цапфи.

Внаслідок дії сили dN на ділянці ds виникає елементарна сила тертя, яка за законом Амонтона—Кулона записується у вигляді

Ця сила створює при обертанні вала протидійний момент тертя 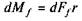, або з урахуванням (6.30) та (6.31) маємо

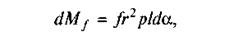
де кут da змінюється від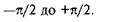

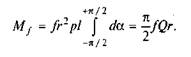Тоді момент тертя в обертовій парі має вигляд

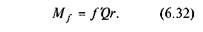Якщо позначити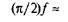 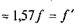— зведений коефіцієнт тертя в обертовій парі, то остаточно дістанемо

Одержана за цим припущенням (р = const) величина моменту тертя добре узгоджується з експериментальними даними для неприпрацьованих(нових) обертових пар. Для припрацьованих (старих) обертових пар більше відповідає друга гіпотеза, згідно з якою знос у напрямку дії сили однаковий. Звичайно, цапфа виготовляється з твердішого матеріалу, ніж підшипник, тому можна вважати, що під час роботи зношується тільки підшипник, а цапфа переміщається в глибину підшипника (на величину зносу) в напрямку дії сили Q. На початку роботи (до зносу) центр цапфи знаходився в точці О (рис. 6.16), через деякий час роботи він перемістився на значення зносу 5 = 00\, на стільки ж перемістилися точки, які лежать на поверхні цапфи, тобто

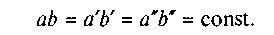
Виділимо біля точки а нескінченно вузьку смужку поверхні цапфи, площа якої 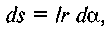де / — довжина цапфи.

Нормальний тиск на цю смужку де с — змінний

нормальний питомий тиск.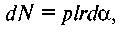

Сила тертя смужки 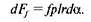Момент тертя смужки

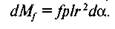Повний момент тертя визначається за формулою

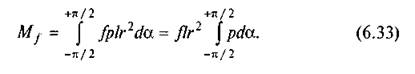Оскільки с — змінна величина, то вона залишилась під знаком інтегралу. Виразимо с через кут а. Постійний знос д = ab у напрямку сили Q і змінний радіальний знос 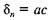зв'язані між собою співвідношенням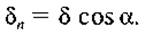

З іншого боку, радіальний знос 5„ буде прямо пропорційний питомому тиску с і відносній швидкості ковзання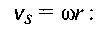

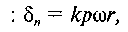де k — невідомий коефіцієнт пропорційності. Отже, 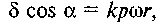звідки

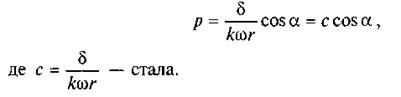
Підставивши значення с у вираз (6.33) і проінтегрувавши, знайдемо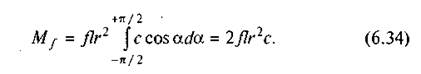

У формулі (6.34) стала с невідома. Щоб визначити її, візьмемо суму проекцій усіх сил на вертикаль: 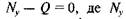— сума

проекцій елементарних реакцій dN на вертикальну вісь:

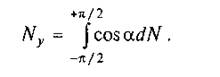
Підставивши в цей вираз значення dN = plrda і с = с cos б, візьмемо інтеграл

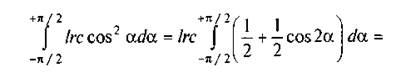
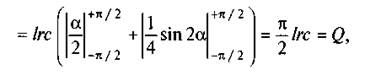
звідки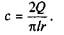

Підставивши с у вираз для моменту тертя (6.34), одержимо

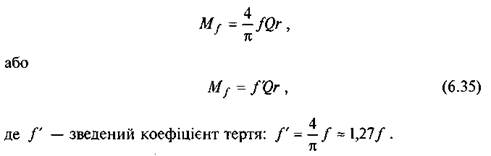
Круг тертя.Якщо цапфа нерухома, нормальна реакція N підшипника проходитиме через цапфи О (рис. 6.17). Коли ж до цапфи прикласти рушійний момент М_р, вона почне обер­татися в підшипнику, і при цьому виникає сила тертя, мо­мент якої і є моментом тертя 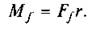Склавши силу тертя

fj з нормальною реакцією N, дістанемо повну реакцію R, яка відхилена від нормальної реакції на кут тертя ц. Момент сили тертя відносно осі цапфи можна виразити також через мо­мент реакції Л:

де с = r sin ц .

Круг радіуса с називають кругом тертя.Повна реакція R завжди дотикається до круга тертя. Круг тертя має всі власти­вості конуса тертя, а саме: якщо рівнодіюча сил, прикладених до вала, проходить поза цим кругом, то вал рухається прискоре­но; коли рівнодіюча сил — дотична, то вал рухається рівномірно або знаходиться в стані спокою, тобто в рівновазі; якщо ж рівнодіюча проходить усередині круга тертя, то вал рухається сповільнено або перебуває в стані спокою.

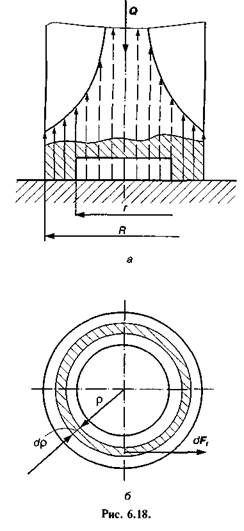
Тертя п'яти в підп'ятнику.Одним із різновидів обертових пар є п'ята, яка при роботі взаємодіє з підп'ятником в умовах тертя ковзання. Опорну поверхню вала можна виготовити у вигляді суцільного круга або кільця, як показано на рис. 6.18, а.

Для визначення моменту тертя в плоскій кільцевій п'яті також користуються двома гіпотезами. Згідно з першою гіпотезою вважають, що питомий тиск с розподіляється рівномірно по поверхні п'яти, тобто

Це буде ближче до істини для неприпрацьованих кінематичних пар та для вужчого кільця, тобто чим менша різниця R — г. Елементарний момент сил тертя dMj на нескінченно вузькому кільці шириною ц (рис. 6.18, б) визначається за формулою

де dF_f— сила тертя, що виникає при обертанні вала в зоні елемен­тарного кільця. Згідно з формулою Амонтона—Кулона маємо

Нормальний тиск, що припадає на це кільце,

де 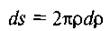— площа кільця.

Підставивши (6.39), (6.40) у формулу (6.38), маємо

Повний момент тертя кільцевої поверхні має вигляд

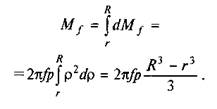
Якщо врахувати (6.37), то остаточно дістанемо

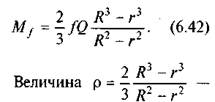
радіус тертя. Тоді

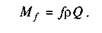
Якщо п'ята буде суцільною, то г = 0, а тому момент тертя має вигляд

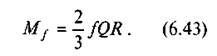
Відповідно до другої гіпо­тези, яка справедливіша для припрацьованих пар, знос у напрямку дії сили Q однако-· вий. У цьому випадку, перш ніж брати інтеграл з функції (6.41), треба виразити с як функцію від р, оскільки

Позначимо знос у напрямку сили 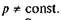Q через д, який у кожній точці кільцевої поверхні буде прямо пропорційний питомому тис­ку і швидкості ковзання v_s= щс, тобто 5 = cpv_s= сдоа> = const, де с — невідомий коефіцієнт пропорційності, звідки

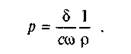
Введемо позначення 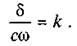Тоді

Підставивши с у вираз (6.41), після інтегрування дістанемо

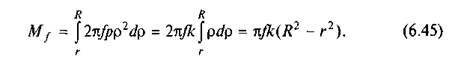
Щоб визначити невідому сталу k, візьмемо суму проекцій усіх сил на вісь вала:

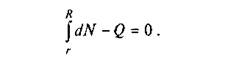
Враховуючи (6.40), одержуємо

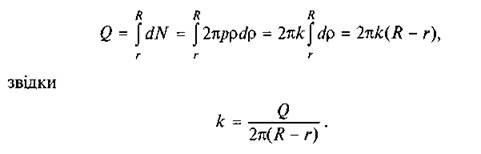
Підставивши k у вираз (6.45), знайдемо момент тертя за другою гіпотезою

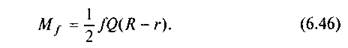
Для суцільної п'яти при г — О момент тертя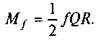

Як показує досвід, суцільна п'ята і підп'ятник зношуються нерівномірно, причому більший знос має місце на більшому радіусі. З умови (6.44) видно, що для суцільної п'яти питомий тиск розподіляється за законом рівнобічної гіперболи (див. рис. 6.18). Очевидно, що при р = 0 теоретично повинно бути 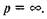Практика підтверджує, що тиск у центрі п'яти дійсно до­сягає досить великих значень. Це викликає зчеплення металу і відокремлення окремих частинок від більш м'якої поверхні. У результаті цього перерозподіляються питомі тиски і вони не досягають тих значень, на які вказує (6.44). Але значні нерівномірності тисків приводять до того, що з часом роботи тертьові поверхні втрачають свою початкову плоску форму.

У кільцевій п'яті знос рівномірніший, що робить її більш вигідною і зручною в експлуатації.