Побудова хеш-функцій на основі ітеративної послідовної схеми

Хеш-функцієюназивають однозначнематематичне перетворення вхідних даних змінного (за звичай, великого) розміру в дані фіксованої довжини. Тоді, хешування(від англ. ‑ hashing) це процедура перетворення вхідного масиву даних довільної довжини у вихідний (частіше – бітовий) рядок фіксованої довжини. Такі перетворення також називаються функціями згортки, а їх результати називають дайджестом повідомлення (від англ. message digest) або хеш-кодом та, навіть, скорочено ‑ хешем,

Криптографічною хеш-функцієюназивають будь-яку хеш-функцію, що задовольняє деякому набору специфічних для криптографічних застосувань вимог. Зокрема, хеш-функція є криптографічно стійкою або безпечною, якщо вона є:

1. Необоротною, тобто теоретично або практично (неможливість обчислити вхідні дані за результатом перетворення). Вимога необоротності або стійкості до відновлення вхідних даних хеш-функції (прообразу) означає, що пошук по заданому значенню хеш-функції h блоку даних M, для якого H(M)=h, є занадто складною обчислювальною задачею;
2. Стійкість до колізій, що означає: два різні набори даних повинні мати різні результати перетворення. При цьому розрізняють стійкість до колізій першого роду, яка означаєнеможливість обчислити (підібрати або відновити)для заданого повідомлення M інше, не співпадаюче з ним, повідомлення N, для якого виконуватиметься рівняння H(N)=H(M). Стійкість до колізій другого роду передбачає обчислювальну неможливість підібрати пару повідомлень (M,M^’), які мають однаковий хеш.

Вказані вимоги не можуть вважатися незалежними, оскільки:

ü Обернена функція нестійка до колізій першого та другого роду.

ü Функція, яка не є стійкою стосовно колізій першого роду, нестійка до колізій другого роду; зворотне невірно.

Слід зазначити, що поки не доведено існування необоротних хеш-функцій, для яких обчислення будь-якого прообразу для заданого значення хеш-функції теоретично неможливо. Тому стійкість хеш-функції у плані находження її прообразу оцінюється лише обчислювальною складністю розв’язання вказаної задачі.

Під час оцінки практичної стійкості враховується, що застосування оптимізованих математичних методів забезпечує більш ефективні обчислення ніж послідовний перебір усіх можливих варіантів розв’язку задачі.

Зокрема, це стосується так званої атаки «днів народження» яка дозволяє знаходити колізії. Вона базується на парадоксі днів народження ‑ твердженні, що в групі з 23 або більше людей ймовірність того, що хоча б у двох з них співпадуть і число, і місяць народження перевищує 50%. На практиці означає що в групі з більш ніж 22 студентів ймовірність хоча б однієї «спільної» дати народження більше ймовірності, що кожного своя дата народження.

Ціллю вказаної атаки є пошук колізії другого роду для заданої хеш-функції 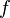. Для этого вычисляются значения 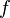для случайно выбранных блоков входных данных до тех пор, пока не будут найдены два блока, имеющие один и тот же хеш. Таким образом, если 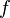имеет 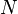различных равновероятных выходных значений и 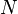является достаточно большим, то из парадокса дней рождения следует, что в среднем после перебора 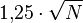различных входных значений будет найдена искомая коллизия. Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно 2^n/2 вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к 2^n/2 .

Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования пользовательских паролей для получения ключей.