Крокові функції стиску та коди автентифікації повідомлень
Досить часто зустрічаються геш-функції, що побудовані у вигляді послідовності ітерацій, на кожному кроці яких застосовуються так звані крокові функції стиску.
Крокові функції являють собою вектор-функції від двох змінних. Їхні аргументи - двійкові вектори, а значення, за звичай, - вектори розмірності 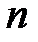 .
.
Розглянемо типові ітеративні геш-функції, для випадку, коли розмірність аргументів 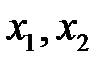 крокової функції
крокової функції 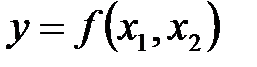 дорівнює довжині геш-коду
дорівнює довжині геш-коду 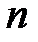 .
.
Для обчислення геш-коду 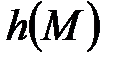 повідомлення
повідомлення 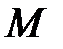 тим, чи іншим, чином доповнюється до довжини кратної
тим, чи іншим, чином доповнюється до довжини кратної 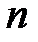 та розділяється на блоки:
та розділяється на блоки: 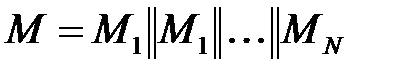 .
.
Далі обчислюється послідовність ітерацій: 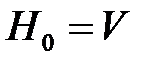 ,
, 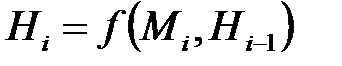 ,
, 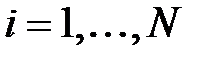 , де
, де 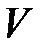 - фіксований несекретний вектор (вектор ініціалізації).
- фіксований несекретний вектор (вектор ініціалізації).
У якості геш-коду приймається значення 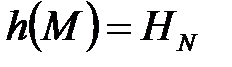 .
.
Очевидно, що при обчисленні геш-функцій можна використати секретний параметр, скажимо, 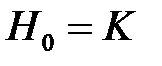 . Відповідні процедури називаються алгоритмами обчислення кодів автентифікації повідомлення. Зустрічається також така назва як ключова геш-функція.
. Відповідні процедури називаються алгоритмами обчислення кодів автентифікації повідомлення. Зустрічається також така назва як ключова геш-функція.
У цих випадках значення 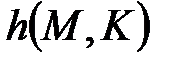 називається кодом автентифікації повідомлення. Код автентифікації зазвичай позначається абревіатурою
називається кодом автентифікації повідомлення. Код автентифікації зазвичай позначається абревіатурою 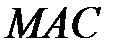 (Message Authentification Code).
(Message Authentification Code).
Прикладом може служити геш-функція, яка ґрунтується на однокроковій функції стиску, що виконує перетворення 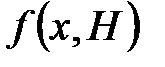 за допомогою блокового шифру
за допомогою блокового шифру 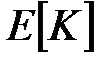 з ключем
з ключем 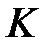 :
: 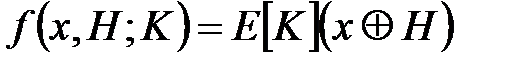 . Процедура обчислення коду автентифікації полягає в наступному.
. Процедура обчислення коду автентифікації полягає в наступному.
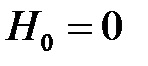 ,
, 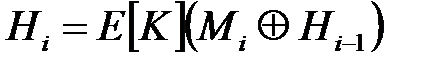 ,
, 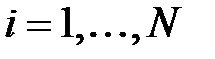 ,
, 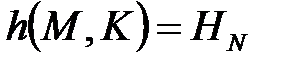 .
.
Виходячи з блокових шифрів можна також будувати геш-функції без секретних параметрів. Для шифрування у якості блоків відкритого тексту можна використовувати як блоки як блоки 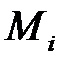 , так і блоки
, так і блоки 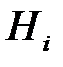 .
.
Аналогічно, будь-який з цих блоків можна використовувати як ключі.
Наведемо дві відповідні крокові функції стиску (аргумент 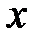 приймає значення відповідних блоків
приймає значення відповідних блоків 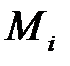 ):
):
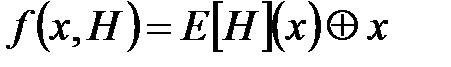 ,
, 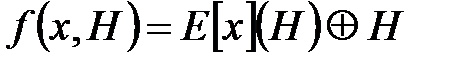 .
.
Деколи, як ключи, замість блоків 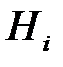 розміру
розміру 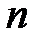 використовуються блоки виду
використовуються блоки виду 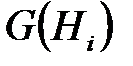 розміру
розміру 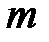 , де
, де 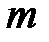 - довжина ключа
- довжина ключа 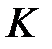 , наприклад,
, наприклад, 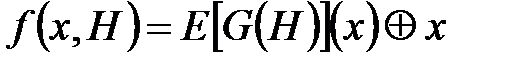 .
.
В стандартизованих геш-функціях, скажимо, SHA-1, ГОСТ 34.311-95, застосовуються складні крокові функції стиску. Зокрема, розмірності аргументів крокової функції не обов’язково однакові і не обов’язково співпадають з довжиною геш-коду.
Взагалі, слід зауважити, що побудова геш-функцій - дуже складна задача.
Низку геш-функцій було дешифровано або знайдено їх слабкі місця вже після їх оприлюднення та практичного використання. Крім того, якщо ітеративна геш-функція використовує стійку крокову функцію, то стійкість самої геш-функції автоматично не гарантується.
Алгоритм НМАС
Стандартизовані геш-функції безпосередньо не передбачають використання секретних параметрів. Разом з тим, бажано мати можливість, за необхідності, застосовувати їх для створення кодів автентифікації, оскільки криптографічна стійкість геш-функцій є високою, а час їхнього обчислення не більший, ніж час шифрування блочним шифром.
У комп’ютерних системах та мережах використовується типовий алгоритм обчислення 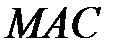 на основі довільної вбудованої геш-функції
на основі довільної вбудованої геш-функції 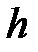 . Стандартне позначення цього алгоритму:
. Стандартне позначення цього алгоритму: 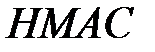 .
.
Вхідні дані алгоритму – повідомлення 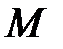 і ключ
і ключ 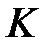 , що розглядаються як рядки бітів.
, що розглядаються як рядки бітів.
Алгоритм обчислення 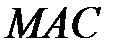 можна записати у виді формули:
можна записати у виді формули:
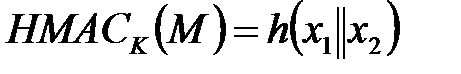 , де
, де 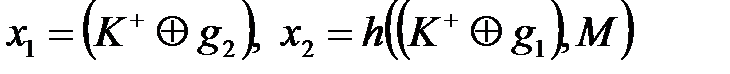 .
.
До повідомлення 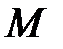 входять біти розширення, що їх можливо вимагає вбудована геш-функція.
входять біти розширення, що їх можливо вимагає вбудована геш-функція.
Нехай кількість 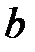 бітів у блоці повідомлення
бітів у блоці повідомлення 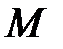 є кратною 8-ми і
є кратною 8-ми і 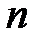 - довжина геш-коду функції
- довжина геш-коду функції 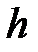 .
.
Якщо довжина ключа 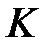 перевищує
перевищує 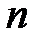 , то застосовується ключ
, то застосовується ключ 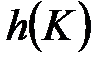 .
.
Довжина ключа 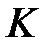 може виявитися і меншою, ніж
може виявитися і меншою, ніж 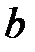 бітів. У цьому випадку, до початку ключа приписуються нулі, у такий спосіб, щоб його довжина дорівнювала
бітів. У цьому випадку, до початку ключа приписуються нулі, у такий спосіб, щоб його довжина дорівнювала 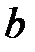 бітів.
бітів.
З урахуванням цих випадків ключ 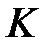 у формулі позначено через
у формулі позначено через 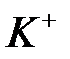 .
.
Рядок 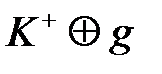 утворюється за допомогою гамування ключа
утворюється за допомогою гамування ключа 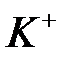 двійковою періодичною гамою
двійковою періодичною гамою 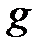 .
.
При цьому, 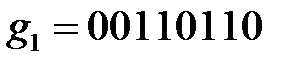 ,
, 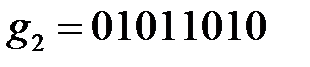 .
.
Алгоритм SHA-1
Алгоритм SHA (Secure Hash Algorithm) є частиною стандарту SHS, що прийнятий АНБ і Національним інститутом стандартів і технологій США (NIST) в 1993г. Для версії SHA-1 довжина геш-коду 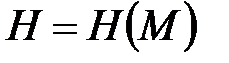 становить 160 бітів.
становить 160 бітів.
У кінець повідомлення 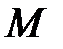 , яке розглядається як рядок бітів, дописується біт, рівний 1. Після цього у кінець повідомлення, за необхідності дописуються нулі, у такий спосіб, щоб довжина отриманного повідомлення, якщо її збільшити на 64, була кратною 512. Далі формується повідомлення, що складається з
, яке розглядається як рядок бітів, дописується біт, рівний 1. Після цього у кінець повідомлення, за необхідності дописуються нулі, у такий спосіб, щоб довжина отриманного повідомлення, якщо її збільшити на 64, була кратною 512. Далі формується повідомлення, що складається з 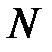 блоків довжиною 512 бітів, в останньому блоці якого зарезервовано поле довжиною у 64 біта. У цьому полі розміщується число, що дорівнює початковій довжині повідомлення
блоків довжиною 512 бітів, в останньому блоці якого зарезервовано поле довжиною у 64 біта. У цьому полі розміщується число, що дорівнює початковій довжині повідомлення 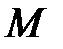 (без врахування дописувань).
(без врахування дописувань).
Розширене повідомлення 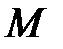 обробляється блоками по 512 бітів. При цьому, окремий блок розглядається як масив, що складається з 16 слів, кожне довжиною у 32 біти.
обробляється блоками по 512 бітів. При цьому, окремий блок розглядається як масив, що складається з 16 слів, кожне довжиною у 32 біти.
Кожний блок обробляється за одну ітерацію (цикл) Обчислення геш-коду здійснюється як послідовність ітерацій з однокроковою функцією стиску 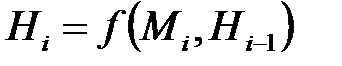 ,
, 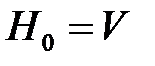 ,
, 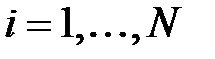 .
.
Блок 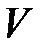 є конкатенацією п’яти початкових зарезервованих значень змінних
є конкатенацією п’яти початкових зарезервованих значень змінних 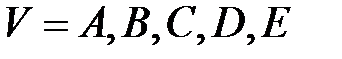 , довжиною у 32 біти, які в системі за основою 16 -мають наступний запис:
, довжиною у 32 біти, які в системі за основою 16 -мають наступний запис:
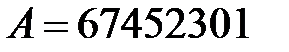 ,
, 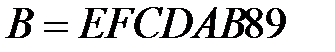 ,
, 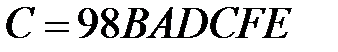 ,
, 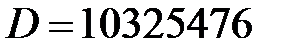 ,
, 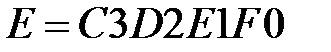 .
.
Після обробки чергового блоку 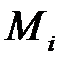 повідомлення
повідомлення 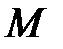 значення змінних
значення змінних 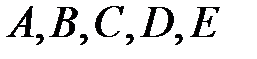 , модифікуються. Результатом роботи кожного циклу
, модифікуються. Результатом роботи кожного циклу 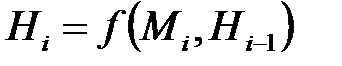 є конкатинація модифікованих значень змінних
є конкатинація модифікованих значень змінних 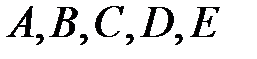 . Результат роботи останнього циклу дає значення геш-коду
. Результат роботи останнього циклу дає значення геш-коду 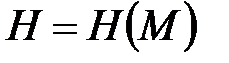 .
.
Таким чином, вхідними даними циклу є блоки 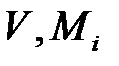 , довжиною 160 та 512 бітів відповідно.
, довжиною 160 та 512 бітів відповідно.
Кожний цикл складається з 80 кроків. На кожному кроці  цикла з номером
цикла з номером 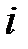 обробляється слово
обробляється слово 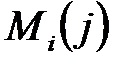 , довжиною у 32 біти.
, довжиною у 32 біти.
На початку кожного циклу створюються копії змінних 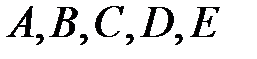 :
: 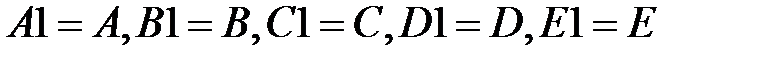 .
.
Слова, що обробляються на циклі 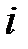 утворюються з блока
утворюються з блока 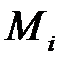 наступним чином.
наступним чином.
1. Блок 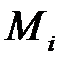 розглядається як послідовність 16 слів
розглядається як послідовність 16 слів 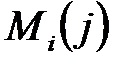 ,
, 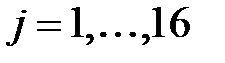 , виходячи з яких, за рекурентним законом формуються інші 64 слова. Рекурентне співвідношення має вид:
, виходячи з яких, за рекурентним законом формуються інші 64 слова. Рекурентне співвідношення має вид:
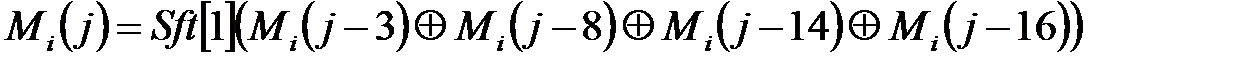 ,
, 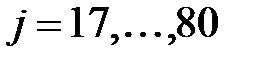 .
.
Тут функція 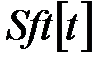 означає циклічний зсув слова на
означає циклічний зсув слова на 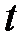 розрядів вліво, а операція Å - порозрядну суму слів за модулем два.
розрядів вліво, а операція Å - порозрядну суму слів за модулем два.
2. Обробка вісьмидесяти слів 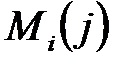 виконується послідовно, групами по 20 слів в групі. Кожній з чотирьох груп відповідають 20 кроків циклу (один раунд):
виконується послідовно, групами по 20 слів в групі. Кожній з чотирьох груп відповідають 20 кроків циклу (один раунд): 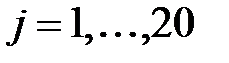 ;
; 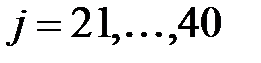 ;
; 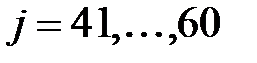 ;
; 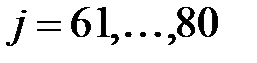 .
.
Крім того, з кожним раундом 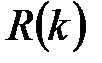 ,
, 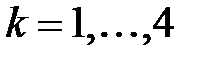 пов’язані константа
пов’язані константа 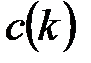 довжиною у 32 біти та функція
довжиною у 32 біти та функція 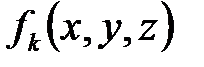 від трьох змінних, кожна з яких є словом тієї ж довжини. При обробці слова
від трьох змінних, кожна з яких є словом тієї ж довжини. При обробці слова 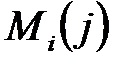 використовуються константа і функція, що пов’язані з відповідним раундом
використовуються константа і функція, що пов’язані з відповідним раундом 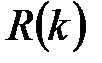 ,
, 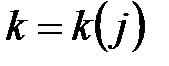 .
.
3. Обробка чергового слова призводить до зміни вмісту слів 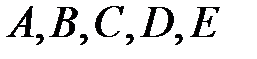 , що виглядає наступним чином:
, що виглядає наступним чином:
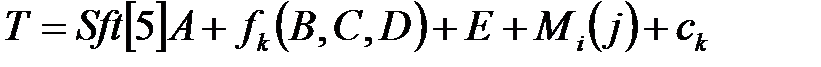 ,
, 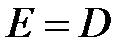 ,
, 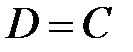 ,
, 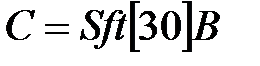 ,
, 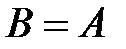 ,
, 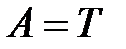 .
.
Тут 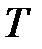 - Допоміжна змінна, а додавання виконується за модулем
- Допоміжна змінна, а додавання виконується за модулем 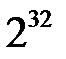 .
.
4. Після 80 кроків обробки блоку повідомлення цикл завершується модифікацією змінних 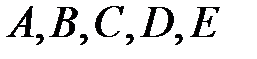 :
: 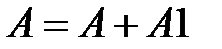 ,
, 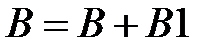 ,
, 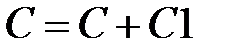 ,
, 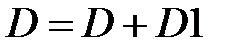 ,
, 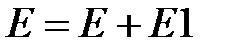 (додавання за
(додавання за 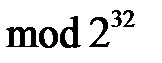 ).
).
Кінець циклу.
Для повноти, приведемо 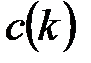 та
та 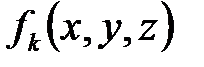 , що застосовуються в раундах
, що застосовуються в раундах 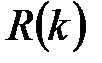 ,
, 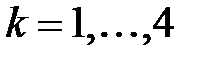 .
.
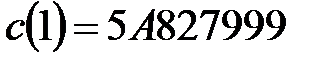 ,
, 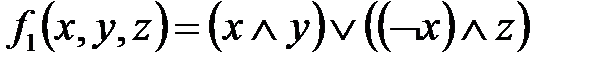 ;
;
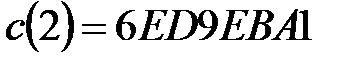 ,
,  ;
;
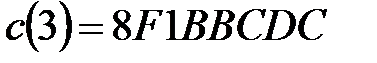 ,
, 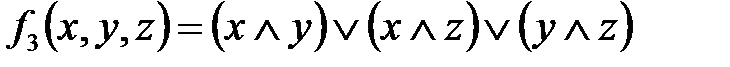 ;
;
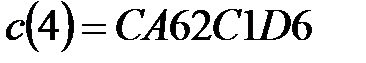 ,
, 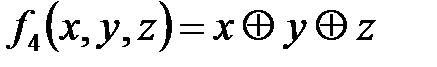 .
.
Дата добавления: 2016-06-15; просмотров: 1379;











