Примеры решения задач.

1. Даны координаты вершин A(1,– 6), B(–3, 0), C(6, 9) треугольника ABC. Составить уравнение окружности описанной вокруг треугольника.

Решение. Для того, чтобы составить уравнение окружности нам необходимо знать ее радиус R и координаты центра О(a, b). Тогда уравнение выглядит так:

(x–a)² +(y–b)² = R² .

Центр окружности, описанной вокруг треугольника находится на пересечении серединных перпендикуляров к сторонам этого треугольника. Находим координаты середин M₁(x₁, y₁), и M₃(x₃, y₃) сторон BC и AB соответственно:

x₁= = = , y₁= = = , M₁ .

Аналогично M₃(–1,–3).

Пусть l₃ – прямая, являющаяся серединным перпендикуляром к AB , а l₁ – к BC. Тогда = (– 4, 6) ^ l₃ и l₃ проходит через M₃ . Поэтому ее уравнение:

– 4(x+1) + 6(y+3) = 0.

Аналогично = (9, 9) ^ l₃ . Поэтому уравнение l₁:

9(x - ) + 9(y - ) = 0

x + y – 6 = 0.

Имеем О = l₁ I l₃. Поэтому, чтобы найти координаты точки О необходимо решить совместно уравнения l₁ и l₃ :

x + y – 6 = 0 ,

– 4x + 6y +14 = 0.

Прибавим ко второму уравнению первое, умноженное на 4:

x + y – 6 = 0,

10y – 10 = 0.

Отсюда y = 1, x = 5, O(5, 1).

Радиус равен расстоянию от О до любой из вершин треугольника. Находим:

R =½½= = .

Значит уравнение окружности:

(x – 5)² + (y –1)² = 65.

2.В прямоугольном треугольнике ABC известныуравнение одного из катетов 3x – 2y + 5 = 0, координаты вершины C(–5,–5) и координаты середины O(–3/2,–3) гипотенузы AB. Найти координаты

вершин A, B и координаты точки E, симметричной O относительно стороны BC. Найти координаты точки пересечения медиан треугольника ABC .

Решение. Пусть катет, уравнение которого нам дано, – это СВ. Он задан общим уравнением вида

ax + by + c = 0.

В данном уравнении геометрический смысл

коэффициентов a и b – это координаты вектора нормали (a, b). Поэтому (3,-2)^ВС.

Составим уравнение перпендикуляра l = ODк стороне СВ и найдем координаты точки D. Вектор будет параллелен OD, т.е. он является направляющим вектором этой прямой. Кроме этого, нам известны координаты точки О на этой прямой. Составляем параметрическое уравнение l :

x = – + 3t, (*)

y = – 3 - 2t .

Имеем D = l I BC. Поэтому, для того, чтобы найти координаты этой точки мы должны решить совместно уравнения l и BC. Подставляем x и y из уравнения l в уравнение BC :

3(– + 3t) –2(–3 -2t)+5 = 0,

– + 9t +6 +4t+5 = 0,

13t = –, t_D= –.

Подставляем найденное t в уравнение l и находим координаты точки D(–3,–2). Для того, чтобы найти координаты E вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это О, вектор скорости – это . Отрезок ОE вдвое длиннее отрезка ОD. Если за время t_D= – мы прошли путь от О до D, то путь от О до E мы пройдем за время t_E= 2t_D= –1. Подставляя это значение в (*), находим E(– 4,5;–1).

Точка D делит отрезок BC пополам. Поэтому

x_D = , y_D = .

Отсюда находим

x_B = 2x_D – x_C = –1, y_B = 2y_D – y_C =1, B(–1, 1).

Аналогично, используя тот факт, что О – середина АВ, находим координаты точки А(-2,-7). Возможен другой путь решения этой задачи: достроить ΔABC до параллелограмма.

Общие формулы деления отрезка в данном отношении выглядят так:

x_С = , y_D = ,

если точка С делит отрезок АВ в отношении l₁:l₂, т.е. ½AC½:½BC½=l₁:l₂.

Известно, что точка пересечения медиан делит медиану в отношении 2:1, считая от вершины. В нашем случае Р делит СО в отношении 2:1. Поэтому

x_P = = = –,

y_P = = = – .

Ответ:А(–2,–7), B(–1, 1), P.

3. Даны координаты вершин A(– 4,–2), B(9, 7), C(2,– 4) треугольника ABC. Составить общее уравнение биссектрисы AD и найти координаты точки D.

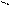
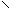Решение. Из курса элементарной математики известно, что = . Вычисляем

(13, 9), (6,–2);

½½= = 5, ½½= = 2 .

Значит BD: DC= 5 : 2 . Далее, применяя формулы деления отрезка в заданном отношении (см. задачу 16) находим

x_D = = = 4,

y_D = = = – , D(4,– ).

Составляем уравнение прямой, проходящей через точки A и D. Для неё вектор является направляющим. Но, в качестве направляющего мы можем взять любой вектор, коллинеарный . Например, удобно будет взять = , (7, 1). Тогда уравнение

AD : = y + 2 Û x – 7y – 10 = 0.

Ответ: D(4,– ), AD: x – 7y – 10 = 0.

4. Даны уравнения двух медиан x – y – 3 = 0, 5x + 4y – 9 = 0 треугольника ABC и координаты вершины A(– 1, 2). Составьте уравнение третьей медианы.

Решение. Сначала мы убедимся, что точка A не принадлежит данным медианам. Медианы треугольника пересекаются в одной точке M. Поэтому они входят в пучок прямых, проходящих через M. Составим уравнение этого пучка:

l( x – y – 3) + m(5x + 4y – 9) = 0.

Коэффициенты l и m определяются с точностью до пропорциональности; поэтому можем считать, что m = 1 (если m = 0 то уравнение пучка задает только первую медиану, а искомая прямая не совпадает с ней). Получаем уравнение пучка:

(l + 5) x + (–l + 4) y – 3l – 9 = 0.

Нам из этого пучка надо выбрать прямую, проходящую через точку A(– 1, 2). Подставим её координаты в уравнение пучка:

– (l + 5) + 2(–l + 4) – 3l – 9 = 0,

– 6l – 6 = 0, l = –1.

Найденное значение l подставляем в уравнение пучка и получаем искомое уравнение медианы:

4x + 5y – 6 = 0.

Ответ: 4x + 5y – 6 = 0.

5.Даны координаты вершин треугольной пирамиды SABC: A(–3, 7, 1), B(–1, 9, 2), C(–3, 6, 6) S(6,–5,–2). Составить уравнение плоскости основания ABC и уравнение высоты SD. Найти координаты точки D и точки S¢, симметричной S относительно плоскости основания.

Решение. Найдем координаты двух векторов параллельных плоскости основания p = ABC:

= (2, 1, 1), = (0,–1, 5).

Уравнение плоскости, проходящей через данную точку A(x_o, y_o, z_o) параллельно двум неколлинеарным векторам (a₁, a₂, a₃), (b₁, b₂, b₃) имеет вид

x – x_o y – y_o z – z_o

a₁ a₂ a₃ = 0.

b₁ b₂ b₃

Подставляем в это уравнение наши данные:

x + 3 y – 7 z – 1

2 2 1 = 0.

0 –1 5

Раскрываем определитель:

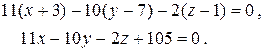
Из уравнения плоскости находим, что вектор (11,–10,–2) является вектором нормали к плоскости. Этот же вектор будет направляющим для прямой h = SD . Параметрическое уравнение прямой, проходящей через данную точку A(x_o, y_o, z_o) с направляющим вектором (a₁, a₂, a₃) имеет вид

x = x_o + a₁t ,

y = y_o + a₂t ,

z = z_o + a₃t .

В нашем случае получаем уравнение:

x = 6 + 11t ,

h: y = –5 – 10t , (*)

z = –2 – 2t .

Найдем основание перпендикуляра. Это точка пересечения прямой 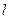с плоскостью p. Для этого мы должны решить совместно уравнения 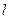и p. Подставляем 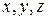из уравнения l в уравнение π:

11(6 + 11t) – 10(–5 – 10 t) – 2(–2 – 2t) + 105 = 0,

66 + 121 t + 50 + 100 t + 4 + 4 t + 105 = 0,

225 y = –225, t = –1.

Найденное t подставляем в уравнение l и находим координаты D(–5, 5, 0).

Вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это S, вектор скорости – это . Отрезок SS¢вдвое длиннее отрезка SD и на его прохождение понадобится вдвое больше времени. Если за время t_D= –1 мы прошли путь от S до D, то путь от S до S¢ мы пройдем за время t¢= 2t_D= –2. Подставляя это значение в (*), находим S¢(–16, 15; 2).

Ответ: ABC: 11x – 10y – 2z +105 = 0, D(–5, 5, 0), S¢(–16, 15; 2),

x = 6 + 11t ,

SD: y = –5 – 10t ,

z = –2 – 2t .

6.Даны уравнения прямой l плоскости p :

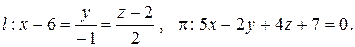
Убедиться, что l и p пересекаются и составить уравнение проекции l¢ прямой l на плоскость. Найти угол между l и p .

Решение. Из уравнения прямой находим ее направляющий вектор: (1,–1, 2) и точку на этой прямой: A(6, 0, 2) , а из уравненияплоскости – векторнормали к плоскости:

(5,–2, 4). Очевидно, что если l½½ p или 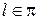, то ^ т.е. · = 0. Проверим:

· = 5·1 – 2·(–1) + 4·2 = 15 ¹ 0.

Значит, l пересекает π. Угол между l и pнаходим по формуле:

sin a = ;

|| = = , || = = = 3 .

Отсюда

sin a = = .

Пусть A_o – проекция точки A на плоскость, а B = lIπ. Тогда l¢= A_oB – это проекция прямой 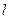. Найдем сначала координаты точки B. Для этого перепишем уравнение прямой l в параметрическом виде:

x = 6 + t,

l: y = – t,

z = 2 + 2t,

и решим его совместно с уравнением плоскости π. Подставляем 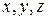из уравнения l в уравнение π :

5(6 + t ) – 2(– t ) + 4(2 + 2t ) + 7 = 0,

30 + 5t + 2t + 8 + 8t + 7 = 0,

15t = – 45, t = – 3.

Подставляя это t в уравнение l находим координаты B(3, 3, 4). Составим уравнение перпендикуляра h = AA_o. Для прямой h вектор служит направляющим. Поэтому h задается уравнением

x = 6 + 5t,

h: y = –2 t,

z = 2 + 4t,

Решаем его совместно с уравнением плоскости π, чтобы найти координаты точки A_o:

5(6 + 5t ) – 2(–2t ) + 4(2 + 4t ) + 7 = 0,

30 + 25t + 4t + 8 + 16t + 7 = 0,

45t = – 45, t = – 1.

Подставляем это t в уравнение h и находим A_o(1, 2,–2). Находим направляющий вектор прямой l' : A_oB(2, 1,–2) и получаем ее уравнение:

.

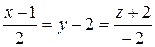7. Прямая l в пространстве задана системой уравнений

2x +2y – z – 1=0,

4x – 8y + z – 5= 0,

и даны координаты точки A(–5,6,1). Найти координаты точки В, симметричной А относительно прямой l.

Решение. Пусть P – основание перпендикуляра, опущенного из точки A на прямую l . Сначала мы найдем координаты точки P. Для этого мы составим уравнение плоскости p, проходящей через точку A перпендикулярно плоскостям p₁ и p₂ . Находим векторы нормали к этим плоскостям: (2, 2,–1), (4,–8, 1). Для плоскости p они будут направляющими. Поэтому уравнение этой плоскости:

x + 5 y – 6 z – 1

2 2 –1 = 0.

4 –8 1

– 6( x + 5) – 6( y – 6) –24( z – 1) = 0 .

Прежде чем раскрывать скобки обязательно

сначала делим все уравнение на – 6:

x + 5 + y – 6 + 4( z – 1) = 0,

x+ y+ 4z – 5 = 0.

Теперь P – точка пересечения плоскостей p , p₁ и p₂ . Для того, чтобы найти ее координаты мы должны решить систему, составленную из уравнений этих плоскостей:

x + y + 4z – 5 = 0,

4x – 8y + z – 5 = 0,

2x + 2y – z – 1 = 0.

Решая ее по методу Гаусса, находим P(1,0,1). Далее, используя тот факт, что P – середина AB мы находим координаты точки B(7,–6,1).

Точку P можно найти другим способом, как ближайшую к A точку прямой l . Для этого необходимо составить параметрическое уравнение этой прямой. Как это делается, см. задачу 10. Дальнейшие действия см. в задаче 8.

8. В DABC с вершинами A(9, 5, 1), B(–3, 8, 4), C(9,–13,–8) проведена высота AD. Найти координаты точки D, составить уравнение прямой AD, вычислить h =½AD½ и проверить h, вычислив S_DABC с помощью векторного произведения.

Решение. Очевидно, что точку D можно найти так: D = π I BC , где π – это плоскость, которая проходит через точку A перпендикулярно стороне BC. Для этой плоскости служит вектором нормали. Находим (12,–21,–12). Координаты этого вектора нацело делятся на 3. Поэтому в качестве вектора нормали к p можем взять = , (4,–7,– 4). Уравнение плоскости π, проходящей через точку A_o(x_o, y_o, z_o) перпендикулярно вектору (a, b, c), имеет вид:

a(x – x_o) + b(y – y_o) + c(z – z_o) = 0.

В нашем случае:

4(x – 9) - 7(y – 5) - 4(z – 1) = 0,

4x - 7y - 4z + 3 = 0,

Составим уравнение прямой BC. Для нее вектор будет направляющим:

x = –3 + 4t,

BC: y = 8 – 7t, (*)

z = 4 – 4t,

Поскольку D = π I BC, для нахождения координат точки D нужно решить совместно уравнения π и BC. Подставляем 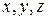из уравнения BC в уравнение π:

4(–3 + 4t ) – 7(8 – 7t ) – 4(4 – 4t ) + 3 = 0,

–12 + 16 t – 56 + 49t – 16 + 16 t + 3 = 0,

81t = 81, t = 1.

Подставляем это t в уравнение прямой BC и находим D(1, 1, 0). Далее, зная координаты точек A и D, составляем уравнение прямой AD вычисляем 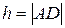по формуле расстояния между точками:

h = = 9.

Далее, S_ΔABC = |´ |; сначала находим сам вектор ´, а потом его модуль.

i j k i j k

´ = –12 3 3 = –27· – 4 1 1 = –27(–i + 4j– 8k) .

0 –18 –9 0 2 1

(В процессе вычисления мы воспользовались свойством определителя: общий множитель элементов одной строки можно выносить за знак определителя).

S_ΔABC = · 27 = .

С другой стороны S_ΔABC = | |·h. Отсюда h = . Находим

| |= = 3 = 27.

Поэтому h = 9. Это совпадает с ранее найденным ответом.

Точку D можно найти, как ближайшую к A точку прямой BC, используя методы дифференциального исчисления. Пусть M(t) – произвольная точка прямой BC; её координаты определяются системой (*):

M(–3 + 4t, 8 – 7t, 4 – 4t).

Находим квадрат расстояние от точки A до M(t):

h²(t) = (9 + 3 – 4t)² + (5 – 8 + 7t)² + (1 – 4 + 4t)²

= (12 – 4t)² + (–3 + 7t)² + (–3 + 4t)² =

= 144 – 96t + 16t² + 9 – 42t + 49t² + 9 – 24t + 16t² =

= 81t² – 162t + 162.

Найдем наименьшее значение функции h²(t) с помощью производной:

h²(t) = 162t – 162; h²(t) = 0 Þ t = 1.

Подставляем это значение t в уравнение прямой BC и находим, что D(1, 1, 0) является ближайшей к A точкой на прямой BC.

9. Исследовать взаимное расположение следующих пар плоскостей (пересекаются, параллельны, совпадают). Если плоскости пересекаются, то найдите угол между ними, если параллельны – расстояние между ними.

а).p₁: 2y + z + 5 = 0, p₂: 5x + 4y – 2z +11 = 0.

Решение. Если плоскости p₁ и p₂ заданы своими общими уравнениями

a₁x + b₁ y + c₁z +d₁= 0, a₂x + b₂ y + c₂z +d₂= 0,

то

p₁½½ p₂ Û = = ¹ ,

p₁ = p₂ Û = = = .

В нашем случае ¹ ¹ , поэтому плоскости не параллельны и не совпадают. Значит, они пересекаются. Угол между плоскостями вычисляется по формуле

cos a = ,

где и – векторы нормали к этим плоскостям. В нашем случае

(0, 2, 1), (5, 4,–2), · = 0·5 + 2· 4 + 1·(–2);

|| = = , || = = 3 .

Значит, cos a = = .

Ответ:a = arccos .

б) p₁: x – y + 2z + 8 = 0,

p₂: 2x – y + 4z –12 = 0.

Решение. Проверяем на параллельность или совпадение:

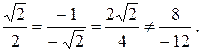
Значит, p₁½½ p₂ но p₁ ¹ p₂. Расстояние от точки A(x, y, z) до плоскости, заданной уравнением 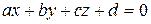находится по формуле

h = .

Выберем точку АÎp₁. Для этого надо подобрать любые три координаты, удовлетворяющие уравнению p₁. В нашем случае, самое простое: A_o(0, 8, 0). Расстояние от A_o до p₂ и будет расстоянием между p₁ и p₂ :

h = = .

10. Составить уравнение плоскости p, которая делит пополам тот из двугранных углов между плоскостями

p₁: 2x – y + 2= 0, p₂: 5x + 4y – 2z –14 = 0,

который содержит данную точку А(0, 3,–2). Составить параметрическое уравнение прямой l = p₁Ip₂ ;

Решение. Если точка 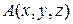лежит на плоскости p, которая делит двугранный угол пополам, то расстояния h₁ и h₂ от этой точки до p₁ и до p₂ равны.

Находим эти расстояния и приравниваем их:

=

Модули мы можем раскрывать с одинаковыми или разными знаками. Поэтому можем получить 2 ответа, т.к. p₁ и p₂ образуют два двугранных угла. Но в условии требуется найти уравнение плоскости, которая делит пополам тот угол, в котором находится точка А . Значит координаты точки М при подстановке в левые части уравнений данных плоскостей p₁ и должны такие же знаки, что и координаты точки А. Легко проверить, что эти знаки для p₁ и «+» для p₂ . Поэтому мы раскрываем первый модуль со знаком «–», а второй – со знаком «+» :

= ,

3(-2x + y - 2) = 5x + 4y – 2z –14,

p:11x + y - 2z - 14 = 0.

Для того, чтобы составить уравнение прямой l, нам нужно найти направляющий вектор этой прямой и точку на ней.

Из уравнений p₁ и p₂ находим координаты векторов нормали к этим плоскостям: (2,–1, 0), (5, 4,–2). Направляющий вектор прямой l перпендикулярен и . Такой можно найти с помощью векторного произведения (по определению, если = ´ , то ^ и ^ ):

i j k

= ´ = 2 –1 0 = 2i + 4j+ 13k .

5 4 –2

Для того, чтобы найти координаты одной точки на прямой, мы должны найти частное решение системы уравнений

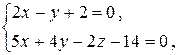
Поскольку уравнений два, а неизвестных три, то система имеет бесконечное количество решений. Нам достаточно подобрать одно. Проще всего положить x = 0 и тогда находим

Þ z = – 3, .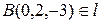

Каноническое уравнение прямой, проходящей через точку B(x_o, y_o, z_o) параллельно вектору (a₁, a₂, a₃), имеет вид:

= = .

В нашем случае имеем уравнение:

l: = = .

Ответ:p: 11x + y – 2z = 0, l: = = .

11. Даны уравнения двух прямых в пространстве:

x = –1 – t, x = –3 + 2t ¢,

l₁: y = 6 + 2 t, l₂: y = –2 – 3t ¢,

z = 5 + 2t, z = 3 – 2t ¢.

Доказать, что данные прямые скрещиваются и составить уравнение их общего перпендикуляра.

Решение. Из уравнений прямых находим координаты их направляющих векторов: (–1, 2, 2), (2,–3,–2) и точек A(–1, 6, 5)Î l₁ , B(–3,–2, 3) Î l₂ . Проверяем и на коллинеарность:

= = .

Значит и l₁ l₂ . Следовательно, прямые l₁ и l₂ либо скрещиваются, либо пересекаются. Мы найдем расстояние между ними, и, если оно не равно нулю, то прямые скрещиваются.

Расстояние вычисляется по формуле

d = .

Находим

I j k

´ = –1 2 2 = 2i + 2j– k; |´ |= = 3.

2 –3 –2

(– 2,– 8,–2) , = – 2·2 – 8·2 – 2·(–1) = –18 , d = .

Вектор = ´ перпендикулярен и перпендикулярен . Сле-довательно, ^ l₁ и ^ l₁, а значит, является направляющим вектором общего перпендикуляра 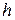к этим прямым. Мы уже нашли его коор-динаты: (2, 2,–1). Для того, чтобы

составить уравнение h нам нужно найти координаты одной точки на этой прямой. Для этого мы составим уравнение плоскости π, проходящей через l₁ и h. Для нее векторы , будут направляющими, и AÎp.

x – 1 y – 2 z – 1

–1 2 2 = 0.

2 2 –1

– 6(x – 1) + 3( y – 2) – 6(z – 1) = 0.

– 2(x – 1) + ( y – 2) – 2(z – 1) = 0.

p: –2x + y – 2z + 2 = 0.

Находим точку пересечения l₂ и π . Для этого 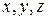из уравнения l₂ подставляем в уравнение π:

–2(–3 + 2t ¢) –2 + 3t ¢ – 2(3 – 2t ¢) + 2 = 0,

6 – 4t ¢ – 2 – 3t ¢ – 6 – 4t ¢ + 2 = 0,

–7t ¢= 0, t ¢= 0.

Подставляем найденное t ¢ в уравнение l₂ и находим, что B(–3,–2, 3) и есть общая точка l₂ и π. Имея точку на h и направляющий вектор этой прямой составляем ее уравнение:

.

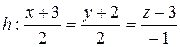Заметим, что прямую h можно задать как пересечение двух плоскостей: плоскости π и плоскости π₁, проходящей через прямую l₂ с направляющим вектором . Этот способ решения также допускается, и он несколько короче.

Второй способ решения этой задачи использует методы дифференциального исчисления. Общий перпендикуляр к двум скрещивающимся прямым – это кратчайший из отрезков, соединяющих две точки на этих прямых. Находим квадрат расстояния от произвольной точки прямой l₁ до произвольной точки прямой l₂ :

h²(t, t¢) = (–3 +2t¢ + 1 + t )² + (–2 – 3t¢ – 6 – 2t)² + (3 – 2t¢ – 5 – 2t)² =

= (t +2t¢ – 2)² + (8 + 2t + 3t¢)² + (2 + 2t + 2t¢)² .

Найдем точку минимума функции h²(t, t¢). Для этого вычисляем частные производные и приравниваем их к нулю:

h²(t, t¢) = 2(t +2t¢ – 2) + 4(8 + 2t + 3t¢) + 4(2 + 2t + 2t¢) = 2(9t +12t¢ + 18);

h²(t, t¢) = 4(t +2t¢ – 2) + 6(8 + 2t + 3t¢) + 4(2 + 2t + 2t¢) = 2(12t +17t¢ + 24);

9t +12t¢ + 18 = 0 t = –2

12t +17t¢ + 24 = 0 t¢ = 0.

Подставляем эти значения t и t¢ в уравнения l₁ и l₂ соответственно и находим, что C(1, 2, 1) и B(–3,–2, 3) являются концами общего перпендикуляра. Остается составить уравнение прямой, проходящей через две точки B и C.

12. Дано уравнение сферы S :

x² + y² + z² +12x -10y – 4z -176 = 0.

а) Составить уравнение плоскости p, проходящей через точки A(–3, 7, 1), B(–1, 9, 2), C(–3, 6, 6)

б) найти координаты центра и радиус окружности, по которой p пересекает S .

Решение. Найдем два вектора параллельных плоскости: (2, 1, 1), (0,–1, 5). Уравнение плоскости, проходящей через данную точку A(x_o, y_o, z_o) параллельно двум данным векторам (a₁, a₂, a₃), (b₁, b₂, b₃) имеет вид

x – x_o y – y_o z – z_o

a₁ a₂ a₃ = 0.

b₁ b₂ b₃

Подставляем в это уравнение наши данные:

x + 3 y – 7 z – 1

2 2 1 = 0.

0 –1 5

Раскрываем определитель:

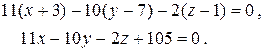
Найдем координаты центра O¢ и радиус 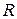сферы. Для этого выделим полные квадраты:

(x² –12x + 36) – 36 + ( y² +10y + 25) + (z² + 4z + 4) – 4 –176 = 0,

(x – 6)² + (y – 5)² + (z + 2)² = 241.

Значит, O¢(6,–5,–2), R = .

Центр окружности, получающейся в сечении сферы плоскостью, является основанием перпендикуляра 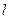, опущенного из центра сферы на плоскость. Из уравнения плоскости находим, что вектор (11,–10,–2) является вектором нормали к плоскости. Этот же вектор будет направляющим для прямой 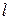. Параметрическое уравнение прямой, проходящей через данную точку A(x_o, y_o, z_o) с направляющим вектором (a₁, a₂, a₃) имеет вид

x = x_o + a₁t ,

y = y_o + a₂t ,

z = z_o + a₃t .

В нашем случае получаем уравнение:

x = 6 + 11t ,

l: y = –5 – 10t ,

z = –2 – 2t .

Найдем основание перпендикуляра. Это точка пересечения прямой 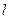с плоскостью p. Для этого мы должны решить совместно уравнения 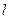и p. Подставляем 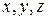из уравнения l в уравнение π:

11(6 + 11t) – 10(–5 – 10 t) – 2(–2 – 2t) + 105 = 0,

66 + 121 t + 50 + 100 t + 4 + 4 t + 105 = 0,

225t = –225, t = –1.

Найденное t подставляем в уравнение l и находим координаты центра окружности: O ²(–5, 5, 0). Находим длину отрезка O ¢O ² как расстояние между точками:

½O ¢O ²½= = 15.

По теореме Пифагора

r² = R² –½O ¢O ²½² = 241– 225 = 16.

Значит, r = 4 – радиус окружности.

Ответ: r = 4, O ²(–5, 5, 0).