Краевые условия (условия однозначности).

Для решения дифференциального уравнения необходимы краевые условия (условия однозначности) при решении задач теплопроводности.

Краевые условия подразделяются:

Геометрические – ими задаются форма и размеры объекта;

Физические условия однозначности – задаются значения теплофизических характеристик вещества ;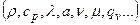

1. Временные или начальные условия – для решения нестационарных задач. Задается закон распределения температуры в начальный момент времени.

4. Граничные условия – условия на границе раздела сред то есть на поверхности объекта. Подразделяются на граничные условия четырех родов.

Граничные условия.

· Граничными условиями первого рода задается закон распределения температуры по поверхности объекта в любой точке поверхности и в любой момент времени.

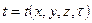
· Граничные условия второго рода – определяют значения плотности теплового потока на поверхности объекта в любой точке и в любой момент времени.

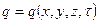
· Граничные условия третьего рода – определяют температуру жидкости омывающей поверхность или закон ее изменения и условия теплообмена на границах раздела сред. Должна быть задана температура и вид теплообмена (t_ж, t_c, a…).

· Граничные условия четвертого рода – условия на границе раздела двух твердых тел. Теплота, подведенная к поверхности одного тела, передается полностью другому телу, имеющему другие характеристики.

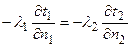
Совокупность дифференциального уравнения теплопроводности и условия однозначности представляют собой полную математическую формулировку задачи.

Рассмотрим пример.