Суперпозиция структур данных
Из рассмотренных структур данных можно создавать различные суперпозиции (вопрос о допустимости той или иной суперпозиции в конкретном языке программирования следует искать в его описании).
Рассмотрим в качестве примера такую часто используемую суперпозицию как файл записей - обычную, например, при создании баз данных. Итак, имеется файл по имени F, содержащий некоторое количество таких записей, как на рис. 1.30. Составим алгоритм подсчета количества болтов, у которых длина (length) заключена в пределах от 3 до 40:
1) положить k = 0 (в конце работы k - число искомых болтов);
2) прочесть первую запись из файла;
3) если В.name = 'болт' и 30 < B.lenght < 40, то увеличить k на 1;
4) если файл уже опустел, то идти к п. 7, иначе - к п. 5;
5) прочесть следующую запись из файла;
6) идти к п.З;
7) конец работы; k - числоискомых болтов.
Стек
Существует (и часто используется) и другая структура данных, в которой тот элемент, который первый в нее помещался, выходит последним и, наоборот, тот, который последним входит, выходит первым (английская аббревиатура «LIFO»). Такая структура получила названиестек (или магазин - по сходству с магазином стрелкового оружия), рис. 1.35.
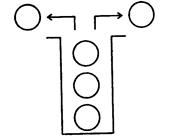
Рис. 1 35. Иллюстрация «стека»
Стеки и принцип LIFO находят очень широкое применение в информатике. Рассмотрим в качестве примера использование стека при вычислении значения арифметического выражения.
Вычисление значения выражения требует соблюдения старшинства операций. Операции по старшинству при вычислении значений математических выражений располагаются в следующем порядке: вычисление значений функций (включая возведения в степень), умножения и деления, сложения и вычитания. Изменить такой «естественный» порядок операций можно с помощью скобок.
Например, вычисление известного из школьного курса математики выражения b2- 4*а*с включает предварительное установление порядка выполнения операций:
14 2 3
b2 – 4*a*c
Для этого выражение просматривают несколько раз. Выполнение каждой операции дает некоторое число, которое приходится записывать отдельно от выражения, запоминая тот фрагмент выражения, для которого число является значением.
Сейчас рассмотрим экономный алгоритм вычисления значения выражения, использующий два магазина для перестановки элементов выражения (с учетом старшинства операций) и для хранения промежуточных результатов. Магазины обозначим M1 и М2, в M1 будут попадать знаки операций, в М2 - числа, участвующие в записи выражения, значения переменных и все промежуточные числовые значения.
Ограничимся выражениями, состоящими только из чисел и переменных без индекса, связанных знаками операций, *, /, +, -. Знак «минус» будет знаком лишь двухместной операции вычитания, выражения типа « - а + I» исключаются из рассмотрения. От этих ограничений можно было бы и отказаться, но это удлинило бы изложение. Пока предположим также, что в выражении нет скобок.
Опишем алгоритм вычисления. Исходное выражение читается слева направо; если прочитано число, то оно заносится в M2, если переменная - в М2 заносится ее значение; если же прочитан знак операции, то необходимо различать несколько случаев.
1) М1 пуст; прочитанный знак помещается на вершину М1.
2) прочитанный знак помещается на вершину M1, если он обозначает операцию, которая старше и поэтому должна выполняться до операции, знак которой был расположен на вершине М1.
3) если операции равноправны или если та, знак которой только что прочитан в выражении, должна выполняться позднее, необходимо применить операцию, знак которой расположен на вершине M1, к двум верхним числам из М2 (число на вершине - второй операнд, число под ним - первый); знак операции на вершине M1 удаляется из M1, вместо двух верхних чисел в M2 помещается результат выполнения над ними операции.
В некоторый момент в исходном выражении не остается символов. Если пуст и M1, то вычисление окончено, результат находится в M2; в противном случае знаки операции извлекаются по очереди из M1 и соответствующие операции применяются к числам из M2.
Рассмотрим вычисление выражения b2 - 4*а*с; значения переменных а, b, с обозначим А, В, С. Знак возведения в степень обозначим, как часто делается, стрелкой вверх.


Про знак операции говорят, что он имеет более высокий приоритет в сравнении с другим знаком, если обозначаемая им операция старше. В других случаях говорят о равных приоритетах или более низком приоритете. Рассмотренные знаки операций распадаются на группы равных по приоритету:
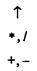
Группы упорядочены по убыванию приоритета.
Теперь дадим правило работы со скобками. Левая скобка заносится в M1 сразу после прочтения. Прочтение правой скобки влечет выполнение всех операций, знаки которых находятся в Mi выше левой скобки; после выполнения этих операций обе скобки уничтожаются. Вот что будет происходить при выполнении (а + b) * с:
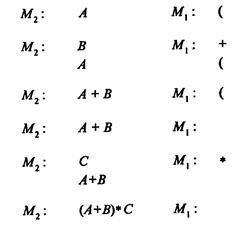
Дата добавления: 2020-02-05; просмотров: 708;











