Прямой и инверсные коды чисел
Различают прямой код числа и инверсные коды, к которым относятся обратный и дополнительный коды.
Прямым кодом двоичного числа называется его изображение в естественной записи, причем в знаковом разряде отрицательного числа записывается единица, а положительного числа – ноль. Таким образом, прямой код двоичной правильной дроби определяется выражением
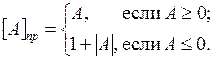
На рис. 1.3 представлена геометрическая интерпретация области чисел и области их изображений в прямом коде.
 |
Таким образом, область положительных чисел совпадает с областью их изображений, а область отрицательных чисел преобразуется в область изображений по формуле 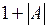 .
.
Ноль в прямом коде имеет два абсолютно эквивалентных значения:
0,000…0;
1,000…0.
При выполнении операции вычитания, заменяемой в вычислительных устройствах операцией сложения чисел с разными знаками, использование прямого кода неудобно, поскольку требуется специальная процедура формирования знака результата. Поэтому для кодирования отрицательных чисел используются так называемые инверсные коды.
Дополнительный код двоичной правильной дроби определяется выражением
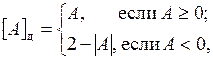
а дополнительный код целого двоичного n-разрядного числа – выражением
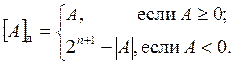
Из приведенных выражений следует, что дополнительный код положительного числа совпадает с его изображением в прямом коде. Дополнительный код отрицательного двоичного числа образуется путем инвертирования всех разрядов прямого кода числа и прибавления к младшему разряду единицы по правилам двоичной арифметики. В знаковый разряд отрицательного числа записывается единица.
Число ноль в дополнительном коде имеет только одно изображение:
0,000…0.
Различают также модифицированный дополнительный код, отличающийся наличием удвоенного знакового разряда. Два знаковых разряда используются для обнаружения переполнения разрядной сетки при выполнении сложения чисел с одинаковыми знаками, модуль суммы которых превышает единицу. Модифицированный дополнительный код определяется выражением
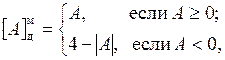
при этом знак положительного числа кодируется двумя нулями, знак отрицательного числа – двумя единицами. Ноль также имеет единственный код
00,000…0.
На рис. 1.4 представлена геометрическая интерпретация области чисел и области их изображений в модифицированном дополнительном коде.
 |
Различают также еще один инверсный код, называемый обратным кодом и определяемый для n-разрядных двоичных правильных дробей выражением
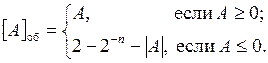
Из приведенного выражения следует, что для положительных чисел обратный код совпадает с прямым кодом. Обратный код отрицательных чисел определяется путем инвертирования разрядов прямого кода и установления единицы в знаковом разряде.
Ноль в обратном коде имеет два значения:
0,000…0;
1,111…1.
Как и в случае дополнительного кода, для обнаружения переполнений можно использовать модифицированный обратный код, отличающийся двойным знаковым разрядом.
Модифицированный обратный код n-разрядной двоичной правильной дроби определяется выражением
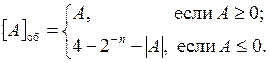
Ноль в модифицированном обратном коде записывается двумя способами:
00,000…0;
11,111…1.
Дата добавления: 2020-02-05; просмотров: 849;











