Первый метод. Оценка суммарной продолжительности работ относительно ведущего потока.
Ведущим потоком плана называют такой частный поток, у которого сумма продолжительностей работ на захватках максимально.
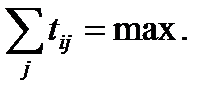
Рассчитывается суммарная продолжительность работ до и после ведущего потока. Для рассмотренного выше примера неритмичных потоков ведущим потоком будет поток 3, у которого сумма продолжительности работ равна 9.
Представим матрицу продолжительностей работ.
| I J | ∑tпред | ∑tпред | Вариант 1* | Вариант 2** | ||||
| I | IV* | III** | ||||||
| II | III* | IV** | ||||||
| III | I* | I** | ||||||
| IV | II* | II** | ||||||
Предлагается следующая последовательность назначения порядка ввода захваток.
1-ая строка матрицы. Сумма продолжительностей предшествующих работ минимальна. Если есть несколько вариантов с одинаковыми значениями суммы предшествующих работ, то выбирается захватка с максимальным значением суммарной продолжительности последующих работ. После принятия решения назначенная строка больше не рассматривается.
Последняя строка матрицы. Сумма продолжительностей последующих работ минимальна. Если есть несколько вариантов с одинаковыми значениями суммы последующих работ, то выбирается захватка с максимальным значением суммарной продолжительности предшествующих работ. После принятия решения назначенная строка также больше не рассматривается.
Затем по указанному алгоритму назначается 2-ая строка, предпоследняя строка и так далее до тех пор пока процесс не сойдется.
Если встречается случай, когда есть несколько строк, у которых суммарные продолжительности одинаковы, то необходимо провести анализ слагаемых. В случае, если суммы получены из одинаковых слагаемых, то выбор порядка ввода захваток безразличен, а если из разных, то целесообразно провести сравнение вариантов. В этом случае полный перебор вариантов обычно невелик.
Данные примера приводят к следующему решению. Предлагается рассмотреть 2 варианта (* и **), так как для захваток I и II сумма «до» равна 4, а «после» 1, но в первом случае 4=3+1, а во втором 4=2+2. Предлагаемая последовательность ввода для вариантов указана ниже:
I* - III, IV* - I, II* - IV, III* - II
I** - III, IV** - II, II** - IV, III** - I
| Захватки (j) | Работы, бригады (i) | |||||||||||
| I* | ||||||||||||
| II* | ||||||||||||
| III* | ||||||||||||
| IV* | ||||||||||||
| Σtij j | ||||||||||||
| Sk | ||||||||||||
| Захватки (j) | Работы, бригады (i) | |||||||||||
| I** | ||||||||||||
| II** | ||||||||||||
| III** | ||||||||||||
| IV** | ||||||||||||
| Σtij j | ||||||||||||
| Sk |
Общая продолжительность работ для первого варианта равна 14, а второго варианта 15, что меньше 18, что дали расчеты исходного варианта.
Таким образом окончательным вариантом ввода захваток можно считать порядок: III, I, IV, II в начальном обозначении захваток.
Для сравнения между собой различных решений построения календарного плана применяются два показателя.
Коэффициент плотности матрицы
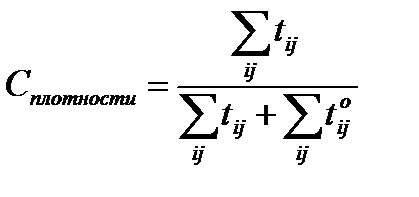
Если сумма значений времени ожидания стремится к нулю (работы ритмичные), то коэффициент плотности стремится к 1. План с большим показателем плотности лучше.
Коэффициент совмещения работ
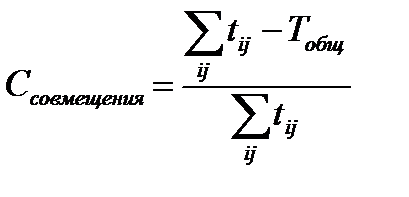
Если сумма значений продолжительностей работ равна общей продолжительности плана (работы выполняются последовательно), то коэффициент совмещения работ равен 0. План с большим показателем совмещения лучше.
Для трех рассмотренных значений плана получены следующие значения коэффициентов:
Исходный план: Сплотности=30/(30+15)=0.67, Ссовмещения=(30-18)/30=0.4.
Первый вариант оптимизации: Сплотности=30/(30+12)=0.71, Ссовмещения=(30-14)/30=0.57.
Второй вариант оптимизации: Сплотности=30/(30+15)=0.67, Ссовмещения=(30-15)/30=0.5.
Расчет подтверждает, что первый вариант оптимизации дал лучший результат.
Дата добавления: 2016-05-28; просмотров: 2825;











