Матричный способ расчёта неритмичных потоков
Необходимо отметить, что неритмичный поток является самым распространенным случаем на практике. Можно предположить, что ритмичный поток может встретиться при строительстве нескольких одинаковых сооружений, когда ритмы работ чудесным образом совпадают, что ожидать на практике сложно. Разноритмичный поток более реален. Он может соответствовать строительству нескольких одинаковых сооружений, но ритмы работ разные. Сохранение ритма на захватках весьма реально, если захватки имеют одинаковый объем работ. Неритмичный поток отражает реальную задачу, когда и объемы работ на захватках и производительность труда для разных работ отличны друг от друга и независимы.
Расчёт продолжительности строительства при неритмичном потоке сводится к нахождению такого совмещения выполняемых работ, при котором организационные перерывы в работе смежных бригад на захватках будут минимальными и в тоже время должны обеспечивать беспрепятственное развитие частных потоков на всех захватках. Захватка, на которой следующий процесс начинается без всякой задержки при беспрепятственном развитии его на всех других захватках, определит место критического сближения двух смежных частных потоков. Если уменьшить или увеличить это сближение, то в первом случае последующий процесс начнётся раньше, чем будет закончен на данной захватке предыдущий процесс; во втором – неоправданно увеличится общий срок строительства.
Как и в случае разноритмичных потоков, сначала рассматривается первый столбец матрицы (1-ый частный поток) и рассчитываются начала и окончания работы на захватках.
Для перехода ко второму столбцу матрицы (2-ому частному потоку) необходимо найти точку критического сближения потоков. Эта точка определяется следующим образом. По приведенной ниже формуле рассчитывается ряд из N (число захваток) чисел для каждой захватки.
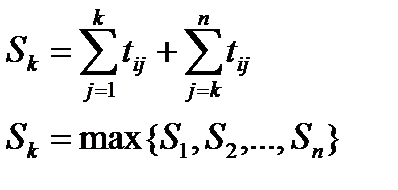
Исходные данные:
| n N | I | II | III | IV |
| Захватки (j) | Работы (бригады) (i) | |||
| I | 2 0 | 4 1 | 3 1 | |
| II | 3 1 | 2 2 | 2 0 | |
| III | 1 2 | 2 2 | 2 1 | |
| IV | 1 3 | 4 0 | 2 1 | |
| Σtij j | ||||
| Sk | 14 13 12 13 12 13 12 12 12 11 14 12 |
S1=t11+t21+t22+t23+t24=2+4+2+2+4=14;
S2=t11+t12+t22+t23+t24=2+3+2+2+4=13;
S3=t11+t12+t13+t23+t24=2+3+1+2+4=12;
S4=t11+t12+t13+t14+t24=2+3+1+1+4=11.
Суммируются последовательно значения продолжительности работ первого столбца по номер индекса k (номера захватки) включительно с значениями продолжительности работ второго столбца, начиная с захватки с номером индекса k. В ряд слагаемых для захватки с номером индекса k входят как значение из первого столбца, так и значение из второго столбца матрицы.
Среди значений полученного ряда чисел выбирается максимальное значение (S3=14). На захватке, соответствующей максимальному значению Sk, произойдет критическое сближение потоков. Следовательно, время ожидания принимается равным нулю, время начала следующей работы на этой захватке будет равно времени окончания предыдущей работы.
ti+1,jн = ti,jк.
После чего расчет может быть продолжен для следующего столбца матрицы.
S1=t21+t31+t32+t33+t34=4=3+2+2+2=13;
S2=t21+t22+t32+t33+t34=4+2+2+2+2=12;
S3=t21+t22+t23+t33+t34=4+2+2+2+2=12;
S4=t21+t22+t23+t24+t34=4+2+2+4+2=14
Завершив расчет всех значений начал и окончаний работ по второму столбцу матрицы, можно приступить к определению захватки, на которой происходит критическое сближение 2-го и 3-его потоков (работ). Используется тот же, выше рассмотренный алгоритм.
Если рассчитанный вспомогательный ряд чисел Sk имеет одинаковое максимальное значение члена ряда, соответствующее двум захваткам. Для дальнейшего расчета можно выбрать любую захватку. Результат расчета будет аналогичным. Обычно расчет начинают с точки критического сближения на захватке с меньшим номером.
Проведя аналогичные расчеты для всех столбцов матрицы (потоков, работ), получают искомый календарный план.
S1=t31+t41+t42+t43+t44=3+1+3+2+3=12;
S2=t31+t32+t42+t43+t44=3+2+3+2+3=13;
S3=t31+t32+t33+t43+t44=3+2+2+2+3=12;
S4=t31+t32+t33+t34+t44=3+2+2+2+3=12.
Дата добавления: 2016-05-28; просмотров: 4403;











