Виды переменных (показателей) в эконометрике
Для построения эконометрических моделей (ЭМетрМ) необходимо определить и тем самым типизировать переменные, которые будут характеризовать экономические показатели и использоваться в ЭМетрМ.
Переменная называется текущей переменной, если её значение используется в модели для данного текущего момента времени t.
В эконометрике экономические переменные объекта подразделяются на виды:
1) экзогенные (независимые);
Экзогенный [гр. exo - снаружи + genesis - происхождение] - имеющий внешнее происхождение, вызываемый внешними причинами
2) эндогенные (зависимые);
Эндогенный [гр. endon - внутри + genesis - происхождение] внутреннего происхождения, вызываемый внутренними причинами.
3) лаговые;
Лаг (от англ. lag, [læɡ] — «запаздывание», «задержка») – запаздывание, экономический показатель, характеризующий временной интервал между двумя взаимосвязанными экономическими явлениями, одно из которых является причиной, а второе - следствием.
Например, существует лаг между началом производственного выпуска товаров и их массовой продажей.
4) предопределенные переменные (объясняющие переменные)
1) экзогенные (независимые);
Экзогенными (независимыми) называются экономические переменные, значения которых определяются вне данной модели. Их значения задаются извне, автономно, в определенной степени они являются управляемыми (планируемыми). Это независимые переменные, обозначаемые обычно буквой x (смотри рисунок Модель типа черного ящика).
2) эндогенные (зависимые);
Термин «эндогенная переменная» означает внутренняя по отношению к моделируемой системе (объекту), т.е. это реакция (состояние) объекта в ответ на внешние (экзогенные) воздействия, задаваемые вектором независимых переменных 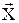 .
.
Эндогенные, т.е. такие переменные, значения которых формируются в процессе и внутри анализируемой модели (явления) под влиянием экзогенных переменных и взаимодействия друг с другом (объясняемые переменные).
Эндогенными являются те переменные, которые в силу принятых концепций определяются внутренней структурой изучаемого явления, иначе говоря, их значения выясняются на основе модели. В свою очередь, экзогенные переменные по определению независимы от структуры явления и их значения (в том числе прогностические) устанавливаются вне модели.
То, как классифицированы переменные (эндогенные или экзогенные) зависит от теоретической схемы или принятой модели. Внеэкономические переменные, например, климатические условия, постоянно бывают экзогенными. В то же время экономические переменные, такие как экспорт и правительственные расходы, могут в одной модели рассматриваться как эндогенные, а в другой – как экзогенные.
3) лаговые;
лаговые– экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например: Yt текущая эндогенная переменная, Yt-1 лаговая эндогенная переменная, – тоже лаговая эндогенная переменная Yt-2;
Модели, включающие лаговые переменные, относятся к классу динамических моделей.
4) предопределенные переменные (объясняющие переменные)
предопределенными переменными (объясняющими переменными) называются лаговые и текущие экзогенные переменные (xt, xt-1), а также лаговые эндогенные переменные (Yt-1).
Ещё раз об аналитическом (формульном виде) эконометрической модели. В полной форме она записывается так:
Y=F(x1,x2,…,xn;a1,a2,…aK)+ε
xi – i-я экзогенная или объясняющая переменная (фактор);
i=1..n, n – число экзогенных переменных;
aj – j-ый параметр модели, j=1..K;
ε – случайный фактор(возмущение) или переменная.
Экономические показатели, которые остаются неизменными при изменении переменных модели, называются параметрами модели или постоянными модели.
Пример.
Y=a1∙x1+a2∙x2+ε (А)
x1 – национальный доход;
x2 – норма процента как инструмент государственного регулирования;
x1 и x2 – экзогенные переменные, известны из статистических наблюдений, т.е. являются исходными данными для модели;
Y – инвестиции, эндогенная или объясняемая переменная. Её значения известны заранее из статистических исследований, но определена с точностью + ε;
a1 и a2 – параметры модели (А).
Задача: зная x1, x2 и Y для предыдущих и текущего периода времени найти:
1) a1 и a2;
2) объяснить или, как говорят, смоделировать предыдущие и текущее значение Y без влияния или возмущения случайного фактора ε;
3) с учетом значений a1 и a2, задавая различные значения x1 и x2, спрогнозировать (предсказать) поведение инвестиций Y в будущие периоды времени без влияния или возмущения случайного фактора ε. В этих расчетах a1 и a2 =const, т.е. будут постоянными значениями.
a1 и a2 называют иногда коэффициентами модели.
Пример 1.1. Предположим, что экономист-теоретик сформулировал следующие положения:
- потребление есть возрастающая функция от имеющегося в наличии дохода, но возрастающая, видимо, медленнее, чем рост дохода;
- объем инвестиций есть возрастающая функция национального дохода и убывающая функция характеристики государственного регулирования (например, нормы процента);
- национальный доход есть сумма потребительских, инвестиционных и государственных закупок товаров и услуг.
Наша первая задача – перевести эти положения на математический язык.
Э-М Модель:
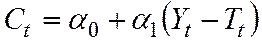 , (1.1)
, (1.1)
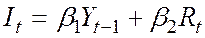 , (1.2)
, (1.2)
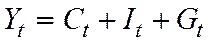 , (1.3)
, (1.3)
где априорные ограничения выражены неравенствами 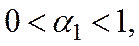
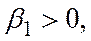
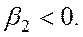
Экономические показатели, которые остаются неизменными при изменении переменных модели, называются параметрами модели.
α и β – параметры модели, которые должны определятся в результате моделирования.
Эти три соотношения вместе с ограничениями образуют модель.
Здесь 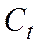 обозначает потребление,
обозначает потребление,
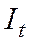 - инвестиции,
- инвестиции,
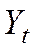 - национальный доход,
- национальный доход,
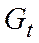 - государственные закупки товаров и услуг,
- государственные закупки товаров и услуг, 
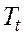 - подоходный налог,
- подоходный налог,
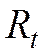 - норму процента как инструмент государственного регулирования, измеренные в момент времени
- норму процента как инструмент государственного регулирования, измеренные в момент времени 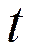 .
.
Уравнения поведения имеют здесь форму точных функциональных зависимостей, однако, как мы увидим позднее, это нереалистично, и нельзя приступать к эконометрическим разработкам, не пользуясь некоторыми дополнительными стохастическими спецификациями.
То есть уравнения (1.1) и (1.2) должны содержать аддитивные случайные составляющие, обусловленные необходимостью учесть влияние соответственно на 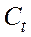 и
и 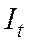 ряда неучтенных факторов.
ряда неучтенных факторов.
Таким образом, для реальной ситуации мы имеем линейную относительно анализируемых переменных и аддитивную относительно случайных составляющих 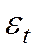 и
и 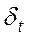 модель:
модель:
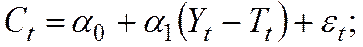 (1.4)
(1.4)
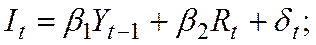 (1.5)
(1.5)
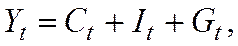 (1.6)
(1.6)
где 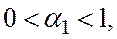
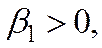
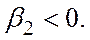
Здесь коэффициенты или параметры
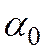 ,
, 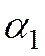 ,
, 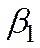 ,
, 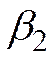
неизвестны до получения «наблюдений» над экономическими переменными.
Проведем классификацию переменных модели:
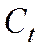 ,
, 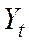 ,
, 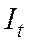 - текущие эндогенные переменные;
- текущие эндогенные переменные;
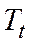 ,
, 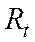 ,
, 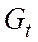 - текущие экзогенные переменные;
- текущие экзогенные переменные;
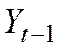 - лаговая эндогенная переменная.
- лаговая эндогенная переменная.
Модель предназначена для объяснения значений эндогенных переменных в текущем периоде времени 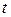 на основе значений, принимаемых экзогенными и лаговыми эндогенными переменными.
на основе значений, принимаемых экзогенными и лаговыми эндогенными переменными.
В более общих ситуациях в модели могут появиться и лаговые значения экзогенных переменных. Оба множества экзогенных (текущих и лаговых) и лаговые эндогенные переменные называют предопределенными переменными.
Порядок проведения эмпирического (эконометрического) исследования можно представить в виде блок-схемы
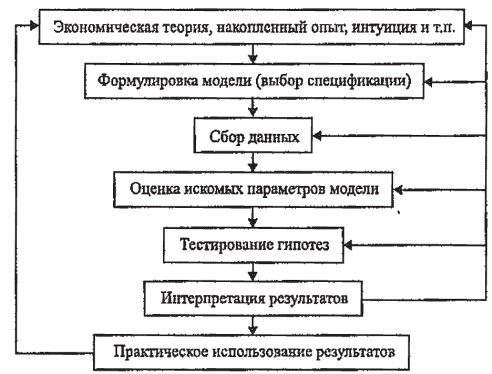
Алгоритм эконометрического моделирования
Согласно приведенному алгоритму, эконометрическое исследование включает следующие 6 этапов

1. Постановочный. Формулировка проблемы (качественный анализ связей экономических переменных – выделение зависимых (yi) и независимых переменных (xik )).
2. Априорный (доопытный). Анализ сущности изучаемого объекта, определение главных и второстепенных факторов, влияющих на проблему. Анализ проблемы с выявлением, какая переменная отражает количественно значение этой проблемы; определить, какие факторы влияют на зависимую переменную – результат.
3. Параметризация (спецификация). Осуществляется выбор общего вида модели, т. е. задается форма связи между зависимой переменной yi и независимыми переменными – факторами xik. Определение такой математической функции, которая должна воспроизводить определенное количество закономерностей зависимой переменной. В итоге подбирается вид функции, адекватно описывающей влияние факторов на зависимую переменную.
4. Информационный. Получение данных, анализ их качества. Проводится визуальных анализ графиков для всех переменных и причинно-следственных связей для определения тенденций и вида зависимостей между переменными. Расчет матрицы парных коэффициентов корреляции и проверка наличия линейной связи между переменными.
5. Идентификация модели. Производится статистический анализ модели и оценка ее параметров. Известно несколько методов оценки параметров, наиболее популярным является метод наименьших квадратов (МНК).
6. Верификация. Осуществляется интерпретация результатов. Проводится проверка истинности (адекватности) модели. С этой целью анализируется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели, какова точность расчетов по этой модели и, в конечном счете, насколько соответствует построенная модель исследуемому реальному экономическому объекту или процессу.
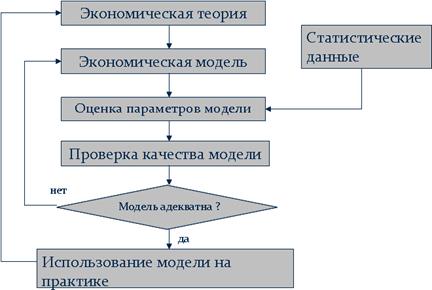
Общая схема построения модели для решения экономической задачи
Типы моделей
Основным этапом эконометрического моделирования является выбор модели. Модель, построенная и верифицированная на основе (уже имеющихся) данных наблюдений над объясняющими переменными, может быть использована для прогноза значений зависимой переменной в будущем или для других наборов значений объясняющих переменных.
Можно выделить три основных класса моделей, которые применяются для анализа и / или прогноза явлений и процессов в экономике.
Модели временных рядов. К этому классу относятся модели:
тренда: 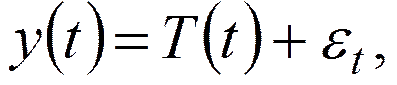
где 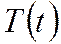 - временной тренд заданного параметрического вида (например, линейный
- временной тренд заданного параметрического вида (например, линейный 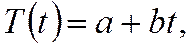 параболический
параболический 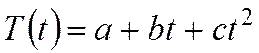 ),
), 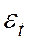 - случайная (стохастическая) компонента;
- случайная (стохастическая) компонента;
цикличность (например, сезонность): 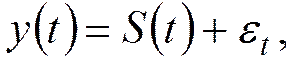
где 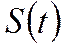 - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента, 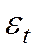 - случайная компонента;
- случайная компонента;
тренда + цикличность: 
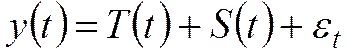 (аддитивная) или
(аддитивная) или
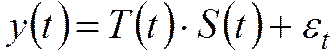 (мультипликативная),
(мультипликативная),
где 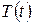 - временной тренд заданного параметрического вида,
- временной тренд заданного параметрического вида, 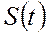 - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента, 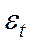 - случайная компонента.
- случайная компонента.
К моделям временных рядов относится множество более сложных моделей, таких как модели адаптивного прогноза, модели авторегрессии и скользящего среднего и др. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования объема продаж авиабилетов, спроса на продукты питания, краткосрочного прогноза процентных ставок и т. п.
Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная 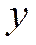 представляется в виде функции
представляется в виде функции
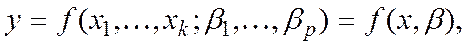
где 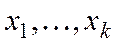 - независимые (объясняющие) переменные-факторы, а
- независимые (объясняющие) переменные-факторы, а 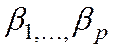 - параметры.
- параметры.
В зависимости от вида функции 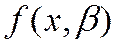 модели делятся на линейные и нелинейные (как по независимым переменным, так и по неизвестным параметрам). Например, можно исследовать спрос на мороженое как линейную функцию от времени, температуры воздуха, среднего уровня доходов. Зависимость же заработной платы от возраста, пола, уровня образования, стажа работы может и не быть линейной.
модели делятся на линейные и нелинейные (как по независимым переменным, так и по неизвестным параметрам). Например, можно исследовать спрос на мороженое как линейную функцию от времени, температуры воздуха, среднего уровня доходов. Зависимость же заработной платы от возраста, пола, уровня образования, стажа работы может и не быть линейной.
Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов. Эта тема является, пожалуй, стержневой.
Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, мы имеем здесь набор объясняемых переменных, связанных через уравнения системы. Примером может служить модель, представленная соотношениями (1.4)–(1.6) (здесь, например, доход 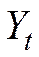 , измеренный в момент времени
, измеренный в момент времени 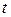 , играет роль объясняющей переменной в уравнении (1.4) и объясняемой переменной в тождестве (1.6)), а также модель спроса и предложения, приведенная ниже. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для макромоделей, моделей страновой экономики и др.
, играет роль объясняющей переменной в уравнении (1.4) и объясняемой переменной в тождестве (1.6)), а также модель спроса и предложения, приведенная ниже. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для макромоделей, моделей страновой экономики и др.
Пример 1.2. Модель спроса и предложения:

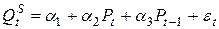 (предложение),
(предложение),
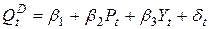 (спрос),
(спрос),
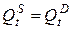 (равновесие).
(равновесие).
Здесь 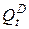 - спрос на товар в момент времени
- спрос на товар в момент времени 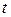 ,
, 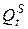 - предложение товара в момент времени
- предложение товара в момент времени 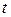 ,
, 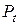 - цена товара в момент времени
- цена товара в момент времени 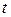 ,
, 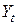 - доход в момент времени
- доход в момент времени 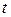 . Цена товара
. Цена товара 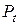 и спрос на товар
и спрос на товар 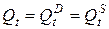 определяются из уравнений модели, т. е. являются эндогенными переменными. Предопределенными переменными в данной модели являются доход
определяются из уравнений модели, т. е. являются эндогенными переменными. Предопределенными переменными в данной модели являются доход 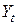 и значение цены товара в предыдущий момент времени
и значение цены товара в предыдущий момент времени 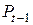 .
.
Дата добавления: 2016-06-15; просмотров: 23654;











