Вывод к. п. д. одинарного полиспаста.

Пусть дан одинарный полиспаст (рисунок 6.6), у которого канат сбегает с подвижного блока. Примем, что к. п. д. блоков известно и к. п. д. подвижных и неподвижных блоков равны.

Обозначим:

h - к. п. д. блока,

h_ПОЛ – к. п. д. полиспаста,

N_ПОЛ – полезная мощность, затрачиваемая на подъем груза,

N_ПОЛН – полная мощность, затрачиваемая на подъем груза,

S_K, u_K – усилие и скорость каната, который наматывается на барабан лебедки,

Q_Г, u_Г – вес и скорость поднимаемого груза,

S₁, S₂, S₃, … S_n – усилия в ветвях каната.

Рисунок 6.6 – Расчетная схема одинарного полиспаста

К. п. д. полиспаста – это отношение полезной мощности к полной мощности, затрачиваемой на подъем груза,

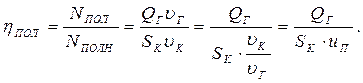(6.10)

Как видно из расчетной схемы полиспаста, представленного на рисунке 6.6, усилие в ветви каната, идущего на барабан лебедки, везде одинаково и составляет S₁=S_K.

Когда канат пройдет через нижний блок, усилие во второй ветви каната будет меньше из-за потерь на трение, которое учитываем к. п. д. блока, тогда S₂=S₁×h=S_K×h.

Когда канат пройдет через верхний блок, усилие в третьей ветви каната будет S₃=S₂×h=S_K×h² и т.д.

Тогда усилие в n-ой ветви каната составит S_n=S_К×h^n-1.

Составим уравнение равновесия системы, представленной на рисунке 6.6,

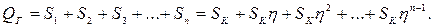(6.11)

Вынесем S_К за скобки:

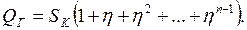
Разделим полученное уравнение на S_К

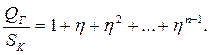
Подставим полученное выражение в уравнение (6.10) и определяем к. п. д. одинарного полиспаста, у которого канат сбегает с подвижной обоймы,

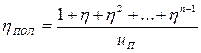. (6.12)

Аналогично можно вывести к. п. д. одинарного полиспаста, у которого канат сбегает с неподвижной обоймы. В результате получим:

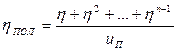. (6.13)

Тогда при одинарном полиспасте усилие в канате, наматываемом на барабан лебедки, с учетом потерь на трение составит:

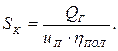(6.14)

При сдвоенном полиспасте усилие в одной ветви каната, наматываемом на барабан лебедки, с учетом потерь на трение составит:

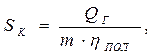(6.15)

где m – число ветвей каната полиспаста, на которых висит груз.