Необходимое условие экстремума

Мордкович: если функция y=f(x)в точке х₀, то в этой точке производная функции равна нулю либо не существует. Теорема не доказывается.

Колмогоров: если точка х₀является точкой экстремума функции f и в этой точке существует производная, то она равна нулю. (Теорема Ферма).

Дано: функция y=f(x), х₀ – точка экстремума.

Доказать: f¢ (x) = 0.

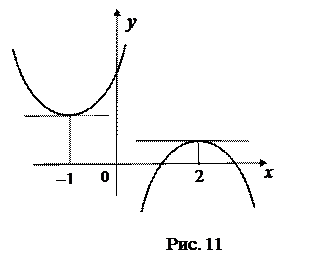
Доказательство

Метод: от противного. Пусть 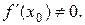Рассмотрим один из противных случаев: f ¢(x)>0. 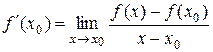. Для значений х достаточно близких к х₀дробь .

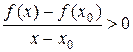Тогда, если x > x₀, то 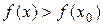; если x < x₀, то 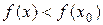, следовательно, x₀ – не является точкой экстремума, что противоречит условию.

Необходимое условие экстремума функции не является достаточным (неверна обратная теорема).

Пример. Функция 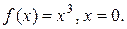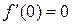, однако, 0 не является точкой экстремума (см. рис.2).

Достаточное условие экстремума.

Теорема (Мордкович):

Пусть функция y = f(x) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х = х₀. Тогда:

1) если у этой точки существует такая окрестность, в которой при 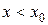выполняется неравенство f¢ (x) < 0, а при 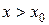выполняется неравенство

f¢ (x) >0, то х₀ – точка минимума функции y = f(x);

2) если у этой точки существует такая окрестность, в которой при 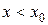выполняется неравенство f¢ (x) > 0, а при х₀ выполняется неравенство

f¢ (x) < 0, то х₀ – точка максимума функции y = f(x);

3) если у этой точки существует такая окрестность, что в ней слева и справа от точки х₀ знаки производной одинаковы, то в точке х₀ экстремума нет.

Истинность этих утверждений становится понятной в связи с монотонность данной функции в окрестности точки х₀.

Учащихся следует убедить в важности условия непрерывности функции в точке х₀.

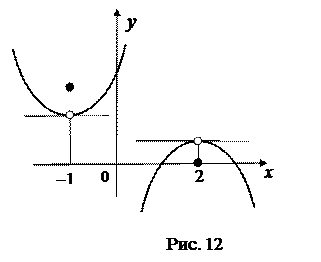
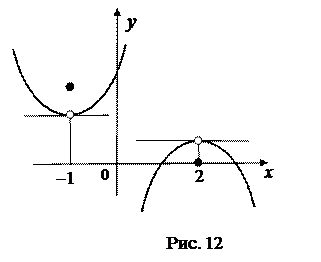
На рис. 12 точка – 1 не является точкой минимума, а точка 2 – точкой максимума. Если бы вырезать чёрные точки да заклеить ими белые, то функции стали бы непрерывными в точках – 1 и 2, тогда бы эти точки были точками экстремума.

Полезно предложить учащимся алгоритм исследования функции на монотонность и экстремумы.

1. Найти производную функции.

2. Найти стационарные и критические точки.

3. Исследовать знак производной в окрестности этих точек.

4. Сделать выводы.

Пример. Исследовать функцию 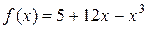на монотонность и экстремумы.

1.

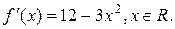
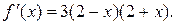
2.

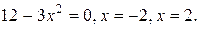
х (-¥;-2) -2 (-2; 2) (2;+¥)

f¢ (x) - + -

f (x) ↓ min ↑ max ↓

-11

3.

4. 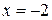- точка минимума, ,

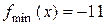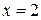- точка максимума, .

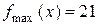Функция убывает на каждом из промежутков (-¥; -2), (2 ;+¥), функция возрастает при хÎ(-2; 2).

Чертежи к лекции

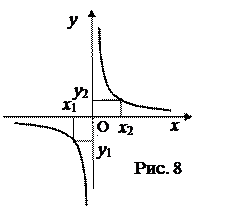
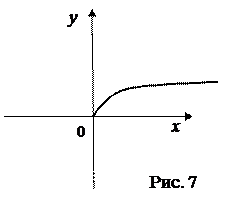
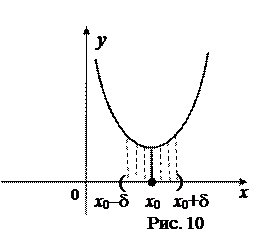
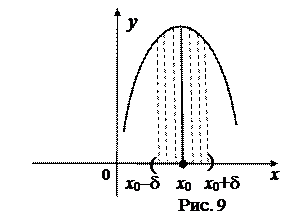
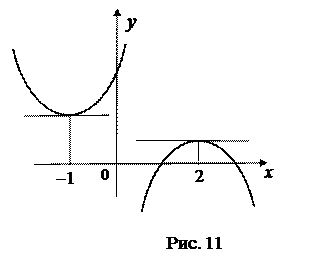
Дата добавления: 2016-06-15; просмотров: 3052;