КОЭФФИЦИЕНТЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ.
Исследованию местных сопротивлений посвящено большое количество работ в основном экспериментальных. Установлено, что коэффициент местного сопротивления 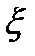 зависит не только от вида самого местного сопротивления, но и от характера режима движения жидкости, т.е. от числа Рейнольдса.
зависит не только от вида самого местного сопротивления, но и от характера режима движения жидкости, т.е. от числа Рейнольдса.
Как показали работы А.Д. Альтшуля, В.Н. Карева, Н.В. Левкоевой и других исследователей, наибольшие значения в зависимости от Re коэффициент 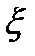 претерпевает в области ламинарного режима. При весьма малых значениях числа Рейнольдса (Re<10) этот коэффициент обратно пропорционален Re.
претерпевает в области ламинарного режима. При весьма малых значениях числа Рейнольдса (Re<10) этот коэффициент обратно пропорционален Re.
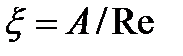 .
.
При больших значениях числа Рейнольдса в области ламинарного режима, зависимость коэффициента местного сопротивления от числа Рейнольдса имеет вид: 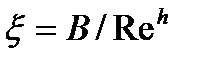 .
.
А и В числовые коэффициенты, зависящие от вида местного сопротивления.
Альтшуль рекомендует определять 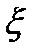 по следующей обобщенной формуле, применимой как при ламинарном, так и при турбулентном режиме
по следующей обобщенной формуле, применимой как при ламинарном, так и при турбулентном режиме
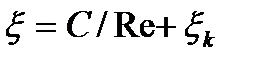 ,
,
где С – коэффициент, зависящий от вида местного сопротивления (по таблице);
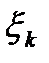 - коэффициент местного сопротивления в квадратичной области турбулентного режима.
- коэффициент местного сопротивления в квадратичной области турбулентного режима.
До настоящего времени вопрос о местных сопротивлениях при ламинарном режиме исследован еще недостаточно полно. Имеющиеся данные, как и приведенные выше формулы, требуют проверки и дальнейшего уточнения.
Значительно более обстоятельно исследован вопрос о местных сопротивлениях при турбулентном режиме. Установлено, что в этом случае изменения коэффициента местного сопротивления 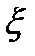 в зависимости от числа Рейнольдса настолько незначительны, что ими можно пренебречь и при практических расчетах
в зависимости от числа Рейнольдса настолько незначительны, что ими можно пренебречь и при практических расчетах 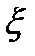 считают зависимым только от характера и конструктивного оформления местного сопротивления.
считают зависимым только от характера и конструктивного оформления местного сопротивления.
Коэффициенты для некоторых видов местных сопротивлений:
1) Выход из труб в резервуар под уровень.
Считая размеры резервуара несравнимо большими, чем сечение трубы, можно принять в формуле (3) скорость 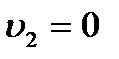 и тогда
и тогда 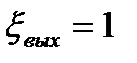 .
.
2) Вход в трубу из резервуара. В этом случае коэффициент местных потерь 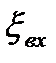 зависит от условий входа. Для трубы выступающей внутрь резервуара
зависит от условий входа. Для трубы выступающей внутрь резервуара 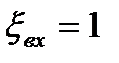 , при острых кромках входа
, при острых кромках входа 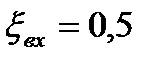 , а при закругленных кромках входа
, а при закругленных кромках входа 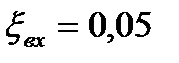 .
.
3) Внезапное расширение. Участки постепенного расширения трубопровода (диффузор),
а так же постепенного сужения (конфузор). Здесь происходит переформирование структуры потока, и в этом случае кроме сопротивления при постепенном расширении и сопротивления входа учитывается коэффициент сопротивления трения 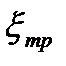 .
.
Местные потери, связанные с изменением направления скорости потока наблюдаются при резком или плавном повороте трубопровода. При этом с увеличением радиуса поворота потери напора уменьшаются.
Местные потери будут на диафрагмах, задвижках, дроссельных затворах, пробковых кранах, шарнирных клапанах с сеткой и обратных клапанах, сетчатых фильтрах, потери при разделении и соединении потоков и др.
При последовательном расположении нескольких местных сопротивлений потери напора от них складываются, однако при их сравнительно близком расположении, ввиду переформирования эпюр распределения местных скоростей по сечению, действительные потери напора могут отличаться от суммы этих потерь. Это объясняется тем, что распределение местных осредненных скоростей после предыдущего сопротивления не успевает стабилизироваться на участке до последующего. Расстояние, на котором сказывается взаимное влияние местных сопротивлений, определяется по рекомендации А. Д. Альтшуля.
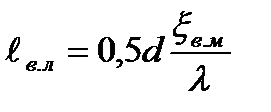
или приближенно 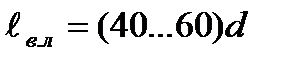 .
.
При расстояниях меньших, чем 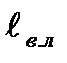 суммарный коэффициент двух местных сопротивлений может быть определен по зависимости
суммарный коэффициент двух местных сопротивлений может быть определен по зависимости
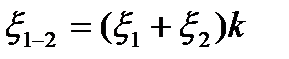 ,
,
где k- определяется на основании опытов.
Во многих случаях при движении жидкостей в различных гидравлических системах имеют место одновременно потери напора на трение по длине и местные потери. Полная потеря напора в подобных случаях определяется как арифметическая сумма потерь всех видов.
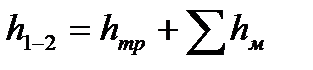 .
.
Дата добавления: 2016-06-15; просмотров: 3671;











