Классификация видов движения жидкости.
Если скорость и давление в каждой точке пространства, заполненного движущейся жидкостью остаются все время постоянными, то движение называется установившемся . Это, есть движение постоянное во времени и изменяющееся в пространстве; при нем скорость и давление зависят от координат движущейся жидкой частицы, т.е. от ее положения в пространстве и не зависят от времени. Таким образом, при установившемся движении
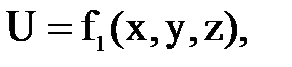
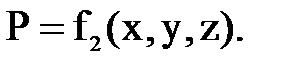
Примером установившегося движения является истечение жидкости из отверстия в стенке или дне сосуда, когда уровень жидкости в этом сосуде все время поддерживается постоянным 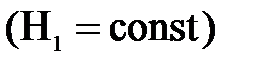 , т.е количество поступающей в сосуд и вытекающей из него жидкости одинаково.
, т.е количество поступающей в сосуд и вытекающей из него жидкости одинаково.
В этом случае форма вытекающей струи, скорость и давление в любом ее сечении остаются неизменными. Если же уровень жидкости в сосуде с течением времени будет меняться 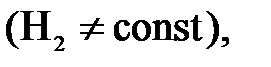 например понижатся по мере вытекания жидкости из отверстия, движение станет неустановившемся, будут меняться скорость истечения жидкости и форма струи.
например понижатся по мере вытекания жидкости из отверстия, движение станет неустановившемся, будут меняться скорость истечения жидкости и форма струи.
Другим примером установившегося движения является движение жидкости в трубопроводе при ее перекачке центробежными насосами. Так как рабочее колесо центробежного насоса практически вращается равномерно с постоянной угловой скоростью, подача жидкости в трубопровод будет происходить так же непрерывно и равномерно, все время в одинаковых количествах, с постоянными скоростью и давлением. Наоборот, при перекачке поршневыми насосами, когда поршень движется с переменной скоростью, имеет место неустановившееся движение, при котором скорость и давление в трубопроводе сменяются во времени.
При изучении потоков жидкости вводят понятия, характеризующие потоки с гидравлической и геометрической точек зрения. Такими понятиями являются: площадь живого сечения, периметр смачивания и гидравлический радиус.
Площадью живого сечения, или живым сечением потока называют площадь сечения потока, проведенную нормально к направлению скоростей элементарных струек , обозначим эту площадь F. В ряде случаев живые сечения потока являются криволинейными.
Живое сечение может быть ограничено твердыми стенками полностью или частично (во втором случае часть живого сечения ограничивается открытой поверхностью жидкости). Если стенки ограничивают поток полностью, движение жидкости называют напорным; в случае частичного ограничения потока движение называют безнапорным. Напорные потоки иногда называют сплошь заполненными, а безнапорные- незаполненными.
Напорное движении характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше последнего.
Примером напорного движения может служить движение жидкости в трубопроводе при ее перекачке насосами, истечении из резервуара или бака, а примером безнапорного- движение жидкости в открытых каналах и реках. Часть периметра живого сечения по которому поток соприкасается с ограничивающими его стенками называют периметром смачивания.
Отношение площади живого сечения к периметру смачивания называют гидравлическим радиусом сечения.
Гидравлический и геометрический радиусы два совершенно различных понятия.
Расходом потока называют количество жидкости, протекающей через поперечное сечение потока в единицу времени. Количество протекающей жидкости, измеренное в объемных единицах ,носит название объемного расхода и обозначается Q. Соответствующую объемному расходу массу жидкости m называют массовым расходом.
Между объемным и массовым расходом существует следующая зависимость 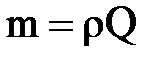 .
.
Наиболее часто применяемые на практике единицы измерения объемного расхода 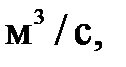
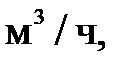
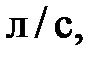
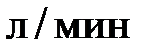 ; единицы измерения массового расхода : килограмм в секунду (кг/с), килограмм в минуту (кг/мин), килограмм в час (кг/ч), тонна в секунду (т/с), тонна в час (т/ч).
; единицы измерения массового расхода : килограмм в секунду (кг/с), килограмм в минуту (кг/мин), килограмм в час (кг/ч), тонна в секунду (т/с), тонна в час (т/ч).
Расход элементарной струйки жидкости может быть определен следующим образом. Обозначим 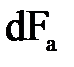 площадь некоторого поперечного сечения струйки а-а. Тогда объем жидкости
площадь некоторого поперечного сечения струйки а-а. Тогда объем жидкости 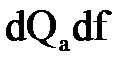 , прошедший через это сечение за весьма малое время dt,будет составлять
, прошедший через это сечение за весьма малое время dt,будет составлять 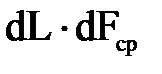 , где dL- расстояние вдоль оси струйки, на которое перемещаются в течение указанного времени частицы жидкости, находящейся в начальной момент времени в сечении а-а;
, где dL- расстояние вдоль оси струйки, на которое перемещаются в течение указанного времени частицы жидкости, находящейся в начальной момент времени в сечении а-а; 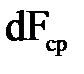 - средняя p на расстоянии dL площадь поперечного сечения струйки.
- средняя p на расстоянии dL площадь поперечного сечения струйки.
Отсюда пишем:
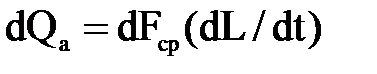
Здесь dL/dt- средняя на участке dL скорость течения жидкости, составляющей элементарную струйку
Будем неограниченно уменьшать промежуток времени dt. Тогда в пределе, при 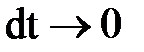 , получим
, получим 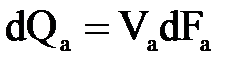 .
.
Поскольку сечение элементарной струйки было выбрано нами произвольно, то, очевидно, dQ=VdF, т.е расход жидкости проходящий через поперечное сечение элементарной струйки равняется произведению площади поперечного сечения струйки на скорость в этом сечении. Уравнение называют уравнением расхода для элементарной струйки.
Если рассматривать поток жидкости как совокупность большого числа элементарных струек, то очевидно, общий расход жидкости Q для всего потока в целом можно определить как сумму элементарных расходов всех отдельных струек, из которых состоит поток 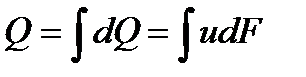 .
.
Чтобы найти эту сумму, необходимо знать закон распространения скоростей в поперечном сечении потока. Поскольку во многих случаях такой закон неизвестен, в общем случае суммирование оказывается невозможным. Поэтому сделаем предположение, что частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью.
Эту воображаемую скорость (с которой должны двигаться через сечение потока все частицы для того, чтобы расход жидкости был равен расходу получаемому при движении жидкости с действительными, неодинаковыми для различных частиц скоростями) называют средней скоростью потока ( 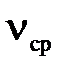 ).
).
Таким образом получаем уравнение расхода для потока в следующем виде: 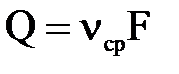 .
.
Из этого уравнения находим 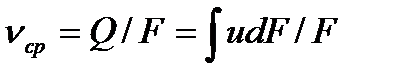 .
.
Если движение жидкости установившееся и при этом размеры и форма сечений вдоль потока не изменяются, следовательно, и средние скорости во всех поперечных сечениях потока одинаковы, движение называется равномерным.
Неравномерным называют такое установившееся движение жидкости, при котором по длине потока изменяются его поперечное сечение и ,следовательно, средняя скорость.
Равномерным, например, является движение жидкости в трубе постоянного диаметра с постоянным расходом жидкости, а неравномерным –движение жидкости в трубе переменного сечения.
Медленноизменяющееся движение- при таком движении кривизна элементарных струек, из которых состоит поток жидкости, весьма незначительна и так же мал угол расхождения между осями отдельных струек. В связи с этим поперечные сечения потока можно рассматривать как плоские сечения, нормальные к оси потока. Распределение давления по сечению при медленн изменяющемся движении подчиняется закону гидростатики. Этому понятию часто соответствует, например, движение в естественных руслах, когда живое сечение изменяется непрерывно, но достаточно плавно вдоль потока.
Дифференциальное уравнение неразрывности жидкости .
Уравнение неразрывности, или сплошности, жидкости основано на законе сохранения массы и исходит из положения механики сплошных сред о том, что внутри движущейся жидкости не может произойти разрыв, не может установиться пустота.
Условие неразрывности может быть представлено в дифференциальной форме для частицы жидкости и элементарной струйки, а так же в конечных величинах для потока жидкости.
В потоке жидкости выделим элементарный объем в форме параллелепипеда с ребрами dx, dy, dz.
Рассмотрим изменение протекающей массы жидкости, которая втекает в левую грань параллелепипеда со скоростью, которую обозначим через 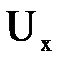 и тогда скорость жидкости, вытекающей из правой грани, можно выразить как
и тогда скорость жидкости, вытекающей из правой грани, можно выразить как 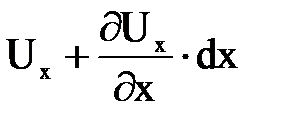 .
.
Принимая плотность жидкости 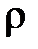 можно записать, что через левую грань за время
можно записать, что через левую грань за время 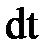 пройдет масса
пройдет масса 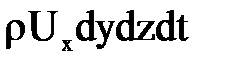 ,
,
А через правую 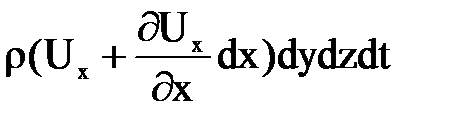 .
.
Разность этих масс составляет 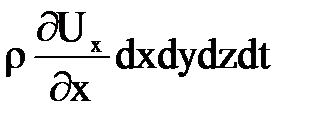 .
.
Рассматривая по аналогии изменение массы жидкости по оси y и z, запишем
- 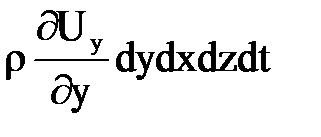 и
и
- 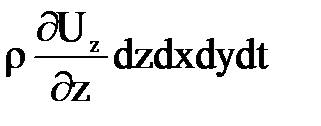 .
.
Закон сохранения массы требует, чтобы общее изменение массы прошедший через выбранный объект, равнялось нулю:
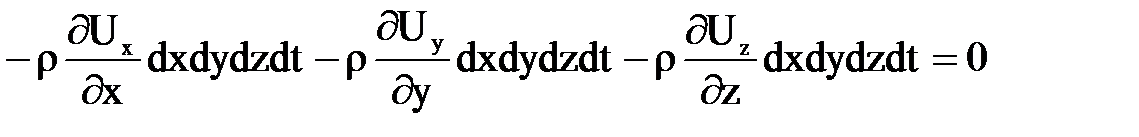 .
.
Отсюда следует, что
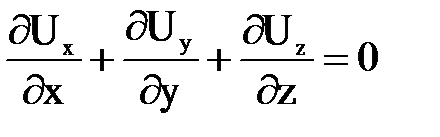 .
.
Это выражение и называется уравнением неразрывности или сплошности в дифференциальной форме для произвольного движения несжимаемой жидкости.
При установившемся движении уравнение неразрывности можно вывести исходя из свойств элементарной струйки.
В соответствии с ними жидкость из струйки не вытекает в стороны и не притекает в нее извне, но в то же время местные скорости разные по длине струйки. Отсюда следует, что количество жидкости, протекающее в струйке в начальном живом сечении и вытекающее из нее в конечном живом сечении, равны между собой и общий объем жидкости в струйке не изменяется.
Рассмотрим живые сечения 1-1 и 2-2 элементарной струйки с местными скоростями соответственно 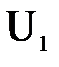 и
и 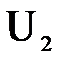 . Объемы жидкости, прошедшие через сечения 1-1 и 2-2 в единицу времени, составляют элементарные расходы
. Объемы жидкости, прошедшие через сечения 1-1 и 2-2 в единицу времени, составляют элементарные расходы 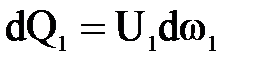 и
и 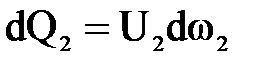 .
.
Ввиду постоянства объема струйки 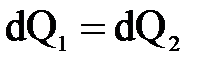 и тогда
и тогда 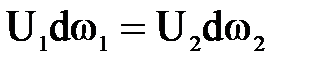 .
.
Это выражение является уравнением неразрывности для элементарной струйки.
Для потока жидкости, представляющего собой совокупность элементарных струек, в соответствии с зависимостью 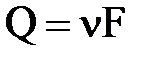
Можно записать, что 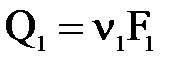 и
и 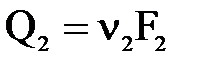 и тогда
и тогда 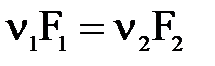 .
.
Это выражение и является уравнением неразрывности или сплошности для потока жидкости. Уравнение можно представить и в таком виде 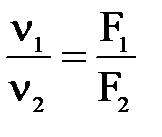 , то есть отношение средних скоростей в живых сечениях потока обратно пропорционально отношению их площадей.
, то есть отношение средних скоростей в живых сечениях потока обратно пропорционально отношению их площадей.
Из этих уравнений следует, что для установившегося движения жидкости- при уменьшении площади живого сечения средняя скорость увеличивается, а при увеличении- уменьшается, а 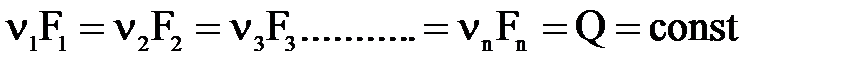 .
.
Дата добавления: 2016-06-15; просмотров: 3401;











