Уравнение движения электропривода

Наиболее удобным методом составления уравнений движения механизмов является метод уравнений Лагранжа второго рода. Сложность уравнения движения будет зависеть от того, какую расчетную схему механической части привода мы выбрали. В большинстве практических случаев выбирают одномассовую, расчетную схему, сводя всю систему электродвигатель-рабочая машина (ЭД-РМ) к жесткому приведенному механическому звену.

Движение одномассовой системы описывается уравнением

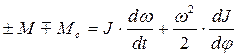, (2.10)

где – электромагнитный момент двигателя;

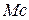– момент сопротивления рабочей машины;

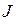– момент инерции, приведённый к валу двигателя

.

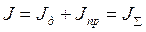При 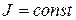, что часто имеет место, уравнение движения имеет вид

.

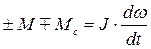Структурная схема соответствующая этому уравнению, будет выглядеть так: (рис. 2.3).

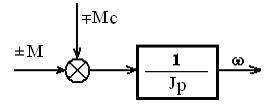
Рис. 2.3. Структурная схема привода

При работе ЭДУ в двигательном режиме М>0, а при работе в генераторном М<0. Если момент М_с является моментом сопротивления, перед ним ставится отрицательный знак, а если движущим – положительный. Для наиболее характерного режима работы ЭП, когда двигатель создает движущий момент, а ИО – тормозящий, уравнение движения выглядит так:

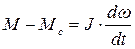. (2.11)

Одномассовая система (жесткое приведённое звено) является интегрирующим звеном. В том случае, когда в кинематической цепи ЭП содержатся нелинейные связи, параметры которых зависят от положения отдельных звеньев механизма (пары кривошип – шатун, кулисный механизм и так далее) движение одномассовой системы описывается нелинейным дифференциальным уравнением с переменными коэффициентами. Входящие в это уравнение моменты в общем случае могут быть функциями нескольких переменных (времени, скорости, угла поворота).

Как следует из структурной схемы, момент двигателя представляет собой управляющее воздействие, а момент сопротивления - возмущающее воздействие.