Моделирование сосудистой системы

Математическое моделирование сосудистой системы сводится в основном к применению фундаментальных физических законов к кровотоку и сосудистой стенке (Б. И. Ткаченко, 1984). На каждую клетку в потоке крови действует локальное напряжение (τ), равное сумме всех сил, исходящих от окружающих элементов и распределенных по его поверхности. Под действием (τ) частицы крови деформируются. Мерой деформации является относительное удлинение (ε), тогда как Δε/dt характеризует скорость деформации. Данные представления лежат в основе моделирования текучести крови при применении к ней закономерностей, характерных для Ньютоновской жидкости. Напряжение, оказываемое на каждую частицу в крупных сосудах, может быть охарактеризовано формулой:

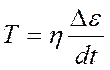
где η - коэффициент пропорциональности, зависящий от состава крови и температуры (вязкость крови).

Исследование модели показало, что вязкость крови зависит еще и от перестроек внутренней структуры потока при ее течении, которое выражается в изменении профиля скоростей соседних слоев. В связи с этим считается, что кровь при определенных условиях обладает свойствами и неньютоновcкой жидкости. Особенно сильно эти свойства проявляются в микроcосудах и при малых скоростях потоков.

При замедлении скорости кровотока происходит переход от ламинарного течения крови к турбулентному, вязкость крови (η) при этом увеличивается, что приводит к увеличению общего периферического сопротивления. При расстройствах регионарного кровотока, например, при шоке, повышение вязкости может способствовать развитию стаза, что приведет к ограничению венозного возврата, а следовательно и сердечного выброса.

При феномене Санарелли-Шварцмана и других видах дисси-минированного внутрисоеудистого свертывания (ДВС) динамическая вязкость крови в микроциркуляторном русле резко возрастает в результате агрегации форменных элементов крови. В то же время вязкость крови в крупных сосудах значительно снижена, текучесть ее увеличена, что приводит к шунтированию кровотока в обход микроциркуляторного русла, и вызывает недостаточность перфузии ткани при относительно высоком уровне венозного возврата.

Другой распространенной математической моделью в гемодинамике является «модель упругого тела». В данном случае упругому телу уподобляется сосудистая стенка. Как упругое тело она подчиняется закону Гука:

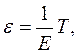
где Е - постоянная (остальные обозначения смотри выше).

Реальная сосудистая стенка обладает еще и вязкими свойствами, то есть для нее:

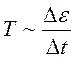
Вязкоупругие свойства стенки сосуда описываются следующей зависимостью:

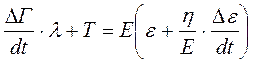
где λ -время спонтанного исчезновения напряжения при неизменной деформации;

η - вязкость сосудистой стенки.

Движение крови по одиночному сосуду математически выражается формулой Пуазейля:

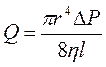
где: ΔР - перепад давлений;

l -длина сосуда;

Q -объемная скорость кровотока (остальные обозначения см. выше).

Так как кровь может рассматриваться как однородная жидкость только в сосудах с радиусом, большим, чем 150 мкм, а в капиллярах мы сталкиваемся с поршневым режимом течения крови, то применимость формулы Пуазейля ограничена.

Среди физических моделей элементов сосудистого русла следует упомянуть модель компрессионной камеры О. Франка. Согласно этой модели крупные артерии могут быть представлены в виде упругого резервуара, на входе связанного с сердцем, а на выходе-с жесткой системой труб, моделирующих периферическое сопротивление сосудов. Тогда:

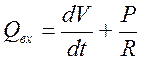
где: Q_вх -ударный объем;

V -объем компрессионной камеры;

Р -давление в ней;

R -сопротивление сосудов, отводящих кровь;

Р/R -расход крови.

Так как 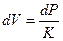где K -коэффициент упругости камеры, то

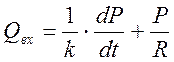
Модель справедливо предсказывает для диастолы экспоненциальное падение Р и Р/R, а для систолы 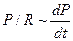. Модель позволяет объяснить постоянство тока крови в мелких сосудах при пульсирующем характере сердечного выброса. О. Франк демонстрирует тип модели с сосредоточенными параметрами сосудистого русла, так как при переходе от одного его отдела к другому свойства системы меняются скачкообразно.

Многие из физических моделей сосудистого русла основаны на «теории подобия». Уравнения, описывающие параметры кровообращения и электродинамические процессы, практически аналогичны.