Движение , форма и гравитационное поле Земли .

Введение.

Основным содержанием курса ”Теория полета” является составление и исследование движения ЛА , изучение общих закономерностей полета , а также его особенностей в различных частных случаях.

Задача исследования полета беспилотного ЛА в общем случае очень сложная ,т.к.

Например ЛА с фиксированными (неподвижными) рулями , как всякое твердое тело имеет 6 степеней свободы и его движение в пространстве описывается 12 дифференциальными уравнениями I-го порядка . Траектория полета реального ЛА описывается значительно большим количеством уравнений .

Ввиду чрезвычайной сложности исследования траектории полета реального ЛА , обычно ее разбивают наряд этапов и исследуют каждый этап в отдельности переходя от простых к сложным .

На первом этапе исследования можно рассмотреть движение ЛА , как движение материальной точки . Известно ,что движение твердого тела в пространстве можно разделить

на :

§ движение центра масс

§ вращение твердого тела вокруг собственного центра масс

Для изучения общей закономерности полета Лав некоторых случаях при определенных условиях можно не рассматривать вращательное движение . Тогда движение ЛА можно рассматривать , как движение материальной точки , масса которой равна массе ЛА и к которой приложены сила тяги , тяжести и аэродинамического сопротивления .

Следует заметить , что даже при такой упрощенной постановке задачи в ряде случаев приходится учитывать моменты сил , действующих на ЛА и потребные углы отклонения органов управления , т.к. в противном случае невозможно установить однозначную зависимость , например , между подъемной силой и углом атаки ; между боковой силой и углом скольжения .

На втором этапе исследуются уравнения движения ЛА с учетом его вращения вокруг собственного центра масс .

Задачей является исследование и изучение динамических свойств ЛА ,рассматриваемого как элемент системы уравнений , при этом главным образом интересуются реакцией ЛА на отклонение органов управления и влияние на ЛА различных внешних воздействий .

На третьем этапе (наиболее сложном) проводят исследование динамики замкнутой системы управления , которая включает в себя наряду с другими элементами и сам ЛА .

Одной из основных задач является исследование точности полета . Точность характеризуется величиной и вероятностью отклонения от требуемой траектории .Для изучения вопросов точности управления движением ЛА необходимо составить систему дифференциальных уравнений , которая бы учитывала все силы и моменты действующие на ЛА , а случайные возмущения . В результате получают систему дифференциальных уравнений высокого порядка , которые могут быть нелинейными , с правильными частями , зависящими от времени , со случайными функциями в правых частях.

Основные задачи решаемые для баллистической ракеты.

1. Исследование летных характеристик ЛА и в первую очередь дальности , в зависимости от конструктивных параметров ЛА с целью выбора наивыгоднейшего сочетания этих параметров .

2. Определение траектории и других характеристик ЛА с известными конструктивными параметрами , с известной системой управления при заданных прицельных дальностях полета для управляемых баллистических ракет .

3. Определение исходных данных для проектирования головных частей и исследование рассеивания головных частей .

4. Обеспечение максимальной прицельной дальности стрельбы в условиях влияния различных возмущающих факторов : разброса конструктивных параметров , изменение внешних условий полета и т.д.

5. Исследование влияния различных возмущающих факторов на активном участке полета ракеты.

6. Определение прицельных данных по заданным координатам точки старта и точки целей .

7. Выбор такой траектории полета , которая обеспечит наилучшее использование возможностей ЛА .

8. Определение исходных данных для летно-конструкторских испытаний и анализ этих испытаний.

При решении этих задач возникает ряд и других вопросов :

§ аэродинамика – определение величин аэродинамических сил , моментов , нагрева поверхности и элементов конструкции ракеты и головной части ( ГЧ ).

§ динамика конструкций – расчет упругих колебаний и колебаний жидкостей в баках .

§ управление полетом ЛА –это обеспечение устойчивости движения , обеспечение управляемости полетом ракеты с учетом упругих колебаний и колебаний жидкости в баках;выбор структуры и основных параметров системы уравнений .

§ динамика неустановившихся режимов –старт ракеты , процессы разделения ступеней , отделение ГЧ (обеспечение безопасности разделения и управляемости ракеты на этих участках полета) .

§ расчет конструкции ЛА на прочность – определение нагрузок , действующих на конструкцию Лана различных участках траектории полета ЛА .

Движение , форма и гравитационное поле Земли .

Движение Земли .

Земля ,при своем движении в космическом пространстве совершает сложное движение , которое состоит из следующих составляющих :

1. вращение вокруг своей оси с запада на восток с периодом 23 часа 56 минут 4.091 секунды среднего солнечного времени ( 89144.091 с ) или 24 ч = 86400 с звездного времени ; угловая скорость вращения Земли при этом равна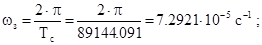

вектор угловой скорости Земли направлен по оси вращения от южного полюса к северному со знаками правой системы координат .

2. Годичные вращения Земли вокруг солнца со средней скоростью Vз=298.93 км/с .

3. Нутационные колебания земной оси с периодом 18.6 года и с амплитудой не превышающей 9.2” (угловых секунд ) . В процессе нутационных колебаний ось описывает конусообразную поверхность вокруг некоторого среднего положения , которое совпадает с вектором кинетического момента Земли .

4. Прецессионное движение Земли относительно оси “эклиптика” с периодом 25800 лет .

5. Движение Земли вместе с солнечной системой относительно других звезд .

Эклиптика - большой круг небесной сферы , по которому происходит видимое годичное перемещение солнца .

Прецессия-движение оси вращения , при котором она описывает круговую коническую поверхность . Одновременно ось может совершать нутационные колебания .

Вращение Земли вокруг своей оси относительно неподвижных звезд определяет звездное время .

Вращение Земли вокруг своей оси относительно центра Солнца определяет истинное солнечное время .

При исследовании движения баллистических ракет все составляющие движения Земли , кроме его суточного вращения не учитываются , т.к. их влияние на траекторию полета ракеты ничтожно мало .При расчете траектории полета зенитной управляемой ракеты ( ЗУР ) Земля считается неподвижной . Считается , что центр Земли движется прямолинейно и равномерно и Земля вращается равномерно вокруг своей оси , положение в пространстве не меняется . Вращение Земли оказывает существенное влияние на динамику полета баллистических ракет ( БР ) , т.к. при движении ракеты необходимо учитывать силы инерции , вызванные суточным вращением Земли .

Форма Земли .

Земля представляет собой геометрическое тело сложной формы .Поверхность Земли , со всеми ее неровностями называется физической поверхностью Земли . Из геометрических тел , описывающих форму Земли наиболее близко к реальной Земле подходит геоид .

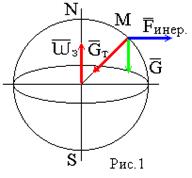Геоид - представляет собой тело ограниченное уровенной поверхностью силы тяжести , совпадающей с поверхностью океана (невозмущенной приливами и волнами) и продолженной под материками . Поверхность геоида непрерывно замкнута и не имеет резких перегибов и складок .

F_инер -сила инерции

Gт -сила притяжения

G -сила тяжести

Примечание : экспериментальным путем невозможно отделить центробежную силу инерции от силы земного притяжения . Известно , что массы пород внутри Земли распределены неравномерно и направление силы тяжести в различных точках Земли зависит от этого распределения , поэтому поверхность геоида является весьма сложной и не имеет математического описания .

В первом приближении Землю можно считать шаром , объем которого равен объему Земли , а радиус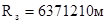

В большинстве случаев с достаточной для практического использования точностью геоид можно заменить эллипсоидом вращения , полученным вращением эллипса вокруг малой оси . Эллипсоид , который наилучшим образом приближается к поверхности реального геоида носит название общего земного эллипсоида .

Он определяется из следующих условий :

§ Центр эллипсоида совпадает с центром Земли , а плоскость его экватора совпадает с плоскостью экватора Земли .

§ Объемы эллипсоида и геоида равны .

§ Сумма квадратов отклонений (по высоте) к поверхности общего земного эллипсоида от поверхности геоида должна быть минимальной .

В настоящее время приняты размеры общего земного эллипсоида :

§ Большая полуось (радиус экватора)

а=6378137 м

§ Малая полуось

b=6356752 м

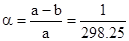-сжатие эллипсоида ;

По мнению ряда ученых поверхность даже самого точного эллипсоида ,правильно ориентированного по отношению к Земле может отклоняться от поверхности геоида на величины 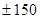м .

В некоторых странах , больших по площади , с целью уменьшения геодезических ошибок , появляющихся от замены геоида общим земным эллипсоидом вводят понятие о референс эллипсоиде . Им называют эллипсоид вращения с соответствующими размерами , определенным образом ориентированным к поверхности Земли и к поверхности которого относятся результаты геодезических работ на рассматриваемом участке земной поверхности в данном государстве .

На территории СССР за размеры референс эллипсоида приняты размеры Красовского :

а=6378245 м ;

b=6357520 м ;

.

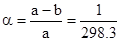Системы координат.