ОСНОВНЫЕ ПОНЯТИЯ О СИМВОЛИЧЕСКОМ МЕТОДЕ.

Символическое изображение векторов переменного тока широко применяется для расчета цепей переменного тока, так как оно дает возможность выразить в алгебраической форме геометрические опе­рации с векторами переменных токов и напряжений, благодаря чему является возможным применить все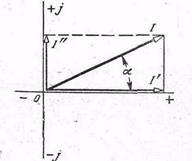

Действительная и мнимая составляющие вектора.

методы расчета цепей постоянного тока (законы Кирхгофа, метод контурных токов, метод наложения и т.д.) для цепей переменного тока.

В основу символического изображе­ния векторов переменного тока приняты следующие простые положения: любой вектор I можно разложить на состав­ляющие (I^/ и I^//), направленные по двум осям прямоугольной системы коор­динат (рисунок). Ось абсцисс при сим­волическом изображении векторов бу­дем называть осью действи­тельных (или вещественных) величин , а ось ординат – осью мнимых величин, причем составляющую вектора по мни­мой оси будем выделять посредством особого множителя — сим­вола j.

Таким образом, в символической форме вектор I будет:

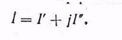
Если некоторый вектор U, направленный по действительной оси, умножить на j, то вектор jU будет повернут по отношению U на 90° против часовой стрелки, т. е. в положительную сторону. Умножение вектора на j² поворачивает вектор на 180°, а такой поворот эквива­лентен перемене знака вектором:j²U=-U Следовательно,j= 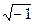, т. е. мнимой единице, в соответствии с чем и дано наиме­нование оси ординат, составляющие векторов по которой сопровож­даются множителем j.Таким образом, при символическом изображе­нии вектор рассматривается как комплексная величина, а плоскость, на которой вектор изображается через действительную и мнимую составляющие, именуется комплексной плоскостью. В соответствии с этим символический метод называют также методом комплексных величин.

Применяются три формы записи комплексной величины, в част­ности вектора переменного тока:

-алгебраическая форма:

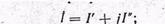
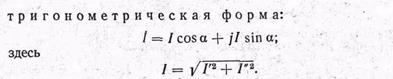
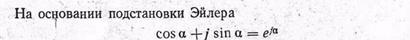
тригонометрическая форма может быть преобразована в показа­тельную форму:

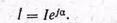
В большинстве случаев можно пользоваться алгебраической фор­мой, но при возведении в степень и извлечении корня целесообразнее применять показательную форму. Для перехода к ней от алгебраи­ческой служат простые соотношения:

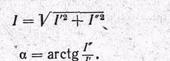
Положение вектора тока или напряжения на комплексной плоско­сти определяется его начальной фазой a, а последняя — относительно произвольна, так как зависит от момента начала отсчета времени. Следовательно, при расчетах цепей переменного тока можно принять равной нулю начальную фазу какого-то одного из напряжений или токов - например известного напряжения на зажимах цепи. Тем самым мы принимаем, что вектор этой величины направлен по дей­ствительной оси. Все остальные векторы, определенные при расчете, окажутся ориентированными по отношению к этому исходному век­тору.

Изображение в символической форме сопротивлений цепи пере­менного тока определяется характером воздействия этих сопротивле­ний на сдвиг фаз между напряжением и током.

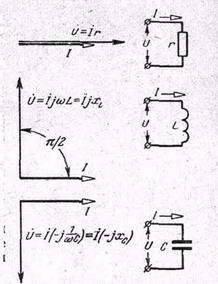
Умножение вектора тока I на активное сопротивление r изменяет только величину вектора, но не его направление (рисунок), так как на участке цепи, содержащем только активное сопротивление, напряжение U=Ir и ток совпадают по фазе, а их векторы направлены параллельно.

Умножение вектора тока I на индук­тивное сопротивление wL = x_l не только изменяет длину вектора, но и поворачи­вает его на 90° в положительную сто­рону, так как на участке цепи, содер­жащем только индуктивное сопротивле­ние, вектор напряжения U=IwL на 90° опережает вектор тока. Следовательно, в символической форме индуктивное реактивное сопротивление изображается положительной мнимой величиной jwL=jx_L.

На основании таких же рассуждений легко найти, что емкостное реактивное сопротивление должно изображаться отрицательной мнимой величиной:

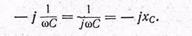
Напряжение на зажимах цепи, содержащей активное и индуктивное сопротивления, соединенные последовательно, запишется в символической форме следующим образом:

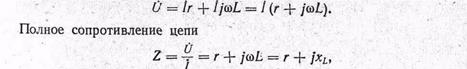
следовательно, это комплексная величина. Ее принято обозначать прописной буквой Z в отличие от строчной буквы

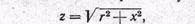
обозначающей модуль полного сопротивления. Часто приходится применять изображение полного сопротивления в показательной форме: