Плоскорадиальный фильтрационный поток

Фильтрационный поток называется плоскорадиальным, когда прямолинейные траектории частиц жидкости, расположенные в горизонтальных плоскостях, являются радиально сходящимися в одной точке каждой плоскости.

Практическим примером такого фильтрационного потока является приток жидкости к одиночной вертикальной скважине, вскрывающей горизонтальный пласт неограниченного простирания на всю его толщину h = const.( рис.9)

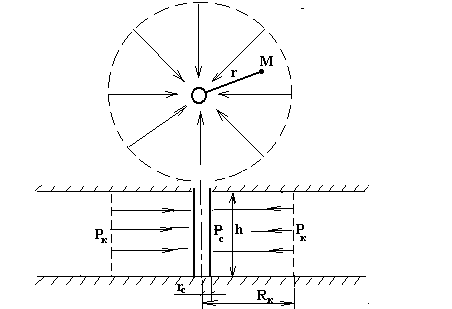
Рис.9

Схемы линий тока в любой горизонтальной плоскости потока будут идентичными, поэтому для исследования рассматриваем движение жидкости в одной горизонтальной плоскости. При установившемся движении жидкости давление Р и скорость фильтрации V в любой точке М зависят только от расстояния r данной точки до оси скважины; поэтому этот поток является всего лишь другим видом одномерного фильтрационного потока.

Решая задачу о притоке несжимаемой жидкости к одиночной скважине, расположенной в центре кругового пласта, используем исходное дифференциальное уравнение фильтрации (3.3), которое в этом случае имеет вид

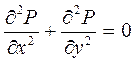. (3.17)

Можно упростить уравнение (3.17), если представить его в полярных координатах r и j . В данном случае вследствие осевой симметрии характеристики потока не зависят от угла j и являются функциями только координаты r . Мы исключаем формальное преобразование координат путем рассмотрения схемы течения в трубке тока переменного сечения (рис. 10).

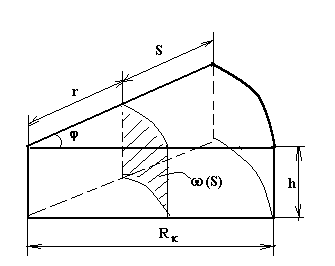Рис.10.

w(S) = w(r) = jrh ; так как r = R-S, поэтому dS = -dr.