Раздел 1.2. Обучение моделированию в процессе изучения математики
Предмет «Математика» в начальной школеявляется основой развития у обучающихся познавательных универсальных учебных действий: логические операции, включая общие приемы решения задач; преобразование информации; моделирование. Обучение математике, на каком бы этапе получения школьного
образования оно не осуществлялось, можно рассматривать как процесс целенаправленного освоения учащимися математической деятельности, важнейшими средствами которой являются модели. Использование моделирования в процессе обучения младших школьников математике является одной из важнейших составляющих обучения, особенно при решении текстовых задач, так как это необходимо не только в качестве основного средства для усвоения математических понятий и знаний, необходимых для развития математического мышления и творческой активности учащихся, а также для формирования умения применять теоретические знания на практике.
Развитие метода учебного моделирования как одного из средств формирования приемов умственной деятельности у младших школьников тесно связано с именем Натальи Борисовны Истоминой, автора учебников математики для начальной школы в системе «Гармония». Н.Б. Истомина в своей концепции развивающего обучения математике отмечала, что наиболее значимым становится «не отработка умения решать определенные типы (виды) текстовых задач, а приобретение опыта в семантическом и математическом анализе различных текстовых конструкций задач и формирование умения представлять их в виде схематических и символических моделей» [7].
По мнению Истоминой Н.Б. схематическое моделирование, применяемое на уроках математики в начальных классах, позволяет наглядно показать существенные связи и отношения между данными задачи и ее искомым, и для построения этих (схематических) моделей учащийся должен несколько раз выполнять операции анализа, синтеза, сравнения, обобщения, абстрагирования и др. Таким образом, в самом процессе построения модели заложены широкие возможности для формирования системы важнейших для обучения приемов умственной деятельности.
Математическая модель – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования – исследовать эти объекты и предсказать результаты будущих наблюдений [8].
Все модели принято делить на схематизированные и знаковые.
В свою очередь, схематизированные модели бывают вещественными (они обеспечивают физическое действие с предметами) и графическими (они обеспечивают графическое действие). К графическим моделям относят рисунок, условный рисунок, чертеж, схематический чертеж (или схему).
Знаковая модель задачи может выполняться как на естественном языке (т.е. имеет словесную форму), так и на математическом (т.е. используются символы).
Выбор модели зависит как от возраста учащихся, содержания задачи, опыта учащихся в построении моделей, развития их творческих способностей, так и от предпочтений учителя.
Для того чтобы решить задачу, учащийся должен уметь переходить от текста (словесной модели) к представлению ситуации (мысленной модели), а от нее к записи решения с помощью математических символов (знаково-символической модели). Осмысление задачи происходит в два этапа.
Первый этап – переход от словесной модели к образу. Трудность данного этапа состоит в том, что ученику надо уметь отвлечься от наиболее бросающихся в глаза свойств предмета или конкретных подробностей текста, то есть абстрагироваться. Именно моделирование помогает учащемуся преодолеть эту трудность.
Второй этап – переход от мысленной модели к знаково-символической. Трудность данного перехода заключается в правильном выборе действия.
Решить задачу – это значит построить логически верную последовательность действий и операций с имеющимися в задаче явно или косвенно числами, величинами, отношениями выполнить требование задачи.
В начальной школе используются разные способы решения текстовых задач: практический, графический, арифметический, алгебраический. При этом большинство задач решается арифметическим способом, который предполагает 4 этапа работы над задачей: усвоение содержания задачи, поиск решения задачи, осуществление плана решения задачи, проверка.
На этапе усвоения содержания задачи основной целью является понимание в целом ситуации, описанной в задаче, условия задачи, требования, смысла всех терминов и знаков, имеющихся в тексте.
Рассмотрим виды графических моделей, используемых на первом этапе, на примере задачи: «Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовал Вова?».
| Модели | |
| предметный рисунок | 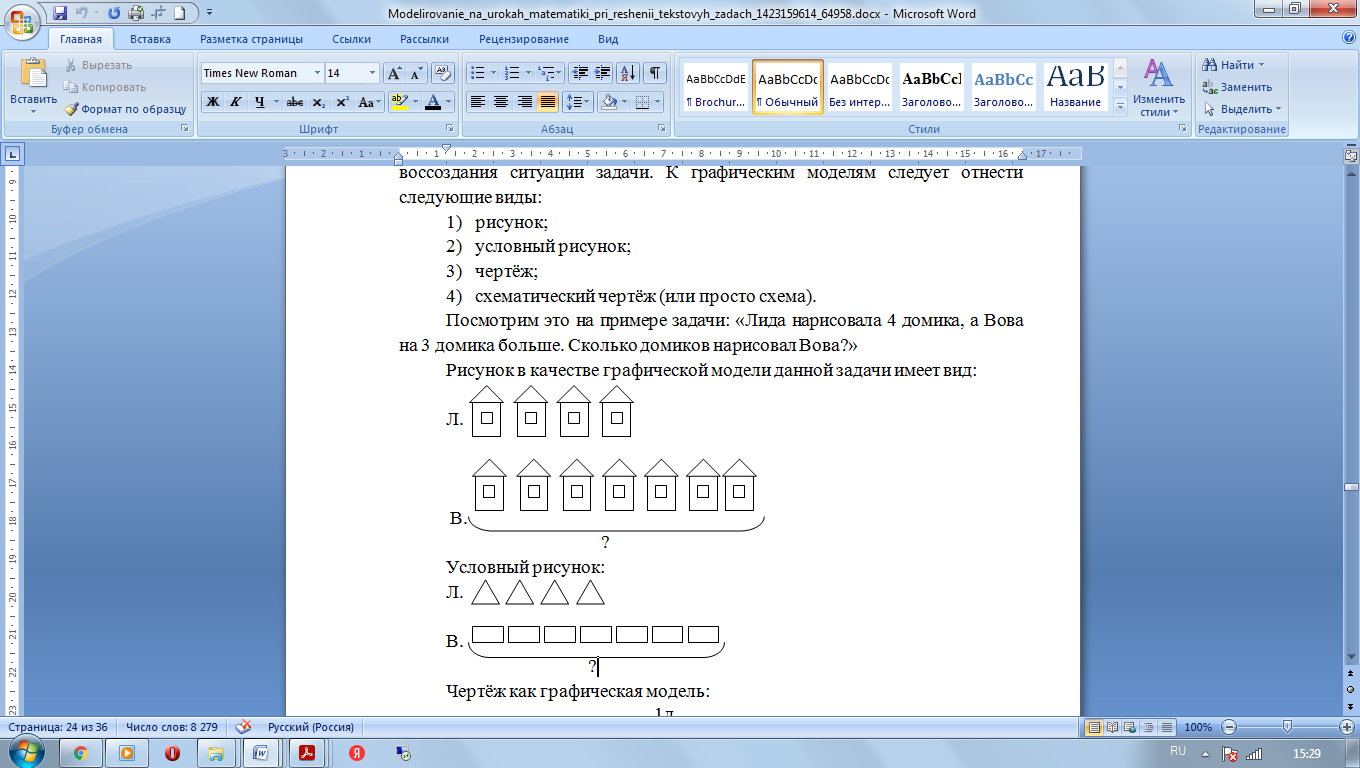
|
| схематичный рисунок | Л. В. ? |
| краткая словесная запись | 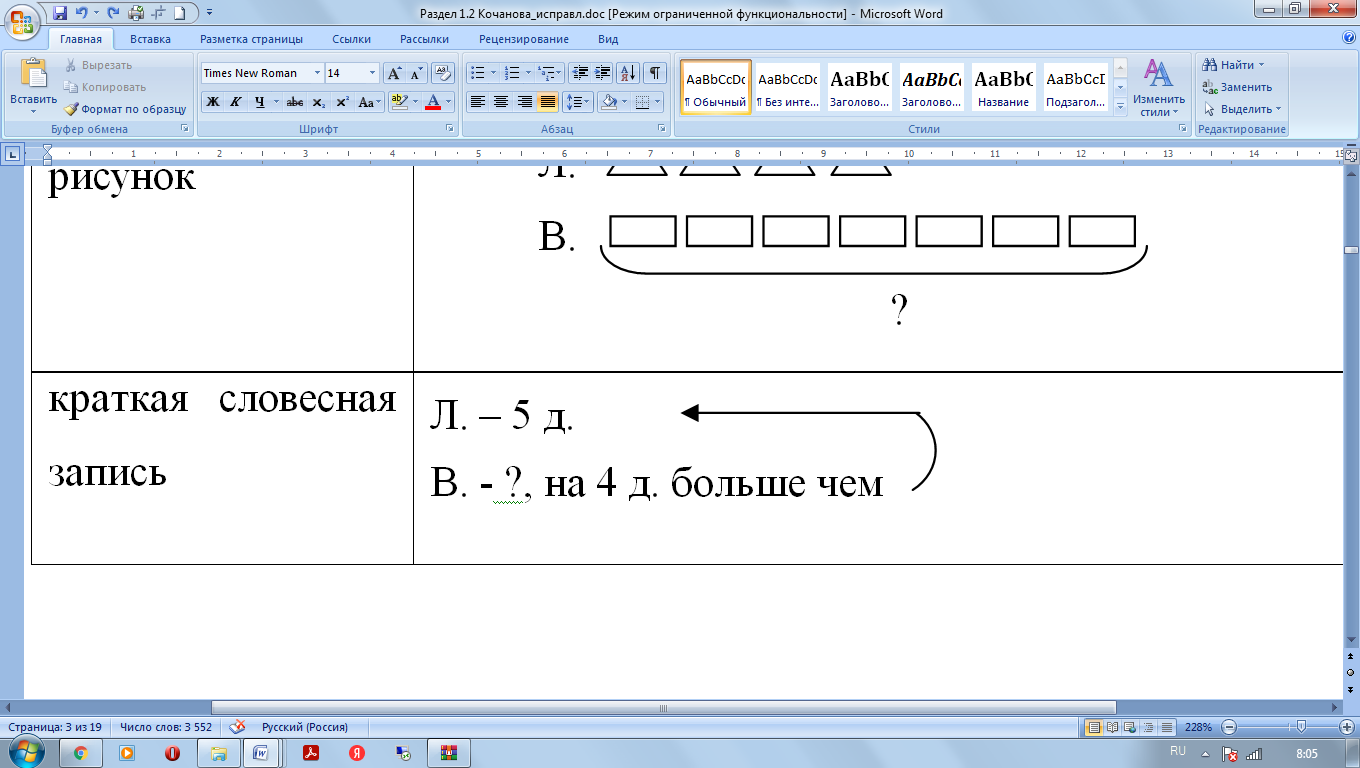
|
| схема | 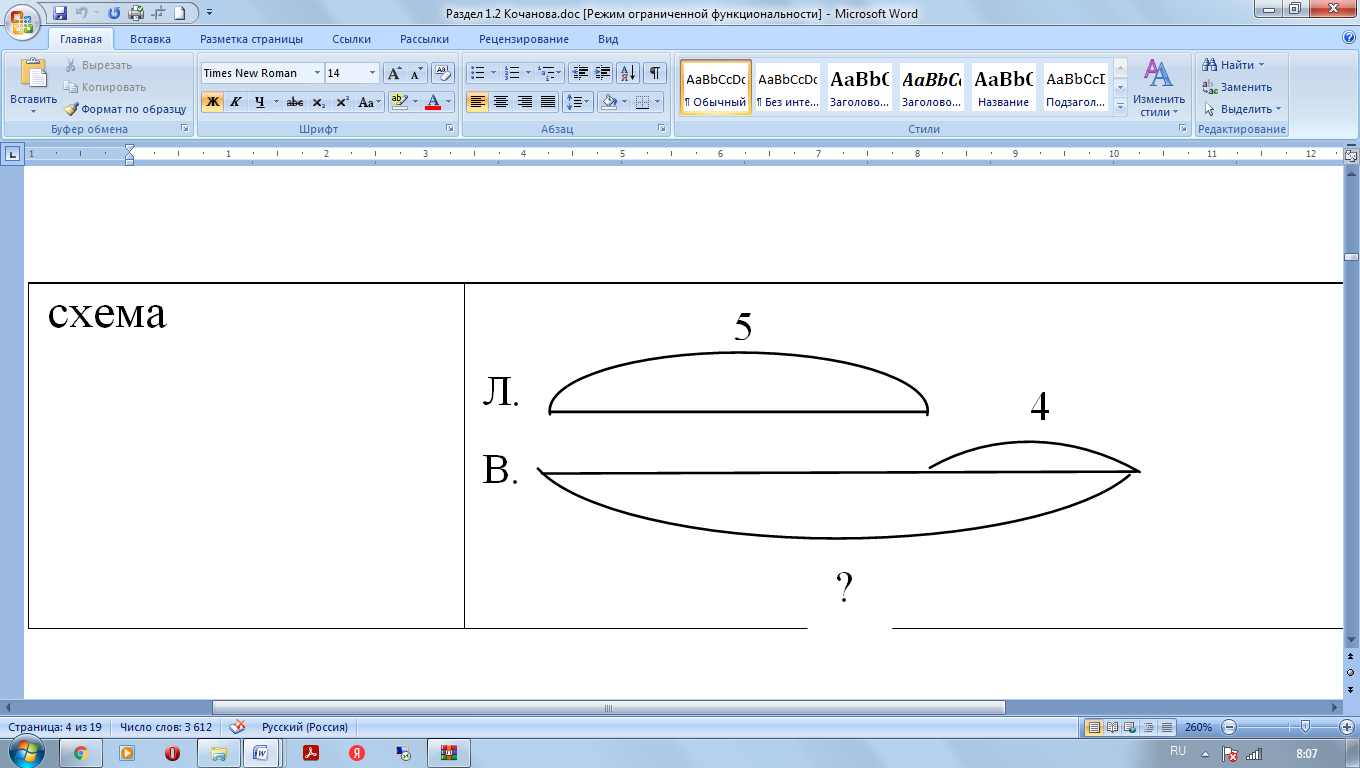
|
Особое внимание следует уделить схеме – чертежу, на которой все взаимосвязи и взаимоотношения величин передаются приблизительно, без соблюдения масштаба. Схема является наиболее предпочтительной моделью при решении задач по ряду причин:
- она исключает пересчет;
- может быть использована при решении задач со сколько угодно большими числами;
- может применяться при решении задач с буквами;
- достаточно конкретна и полностью отражает внутренние связи и количественные отношения в задаче;
- позволяет подняться на достаточно высокую ступень абстрактности: не отражает никаких отношений, кроме количественных;
- все второстепенные детали опущены;
- выбор действия производится без учета главного слова, а только исходя из логики происходящих изменений, которые отражены в модели;
- внешняя схожесть схем подчеркивает однотипность рассуждений при поиске решения задач.
Для формирования действия моделирования С.П. Баранов предложил несколько этапов: замещение, кодирование и декодирование. [5]
1 этап - замещение является основополагающим этапом в формировании действия моделирования у младших школьников: с помощью знаково-символических средств учащиеся усваивают механизм замещения реального предмета или явления на модель. В результате этого ученики получат образ-заменитель оригинала. В математике выделяют несколько видов образов-заменителей, их можно объединить в несколько групп:
1. Заместители (точки, цветы, фигуры и т.д.).
2. Знаки, обозначающие свойства предметов (фишки, контур фигуры и т.д.).
3. Символы, используемые для замещения отношений (>, <; =; =>; ≠) [3].
На этапе кодирования происходит переход текстовой информации на язык знаков. Данный этап включает два уровня: графический и вещественный. Для эффективного усвоения детьми действия кодирования педагог может использовать разноплановые операции, с помощью которых дети будут постепенно осваивать данное действие.
1 шаг − преобразование модели, а именно, достраивание модели и удаление лишних элементов.
• Достраивание модели.
Задача 1. В реке плавало 3 щуки и столько же лещей. Сколько всего рыб плавало в пруду?
| щуки - лещи - ? |
• Удаление лишних элементов.
Задача 2. Бабушка приготовила 6 пирожков, а Лена на два пирожка меньше. Сколько всего пирожков они приготовили?
Л. |
После проведения анализа задачи учащиеся делают вывод, что данная модель не соответствует условиям задачи. Количество фигур, заменяющих пирожки, изготовленные Леной, не соответствует данным задачи. Учащиеся должны убрать или зачеркнуть лишние элементы.
2 шаг − работа по расшифровке модели.
Задача 3. В автобусе может ехать водитель и еще 22 человека. Сколько всего людей может ехать в автобусе?
Запишите выражение, соответствующее данной модели.
| ? |
3 шаг − видоизменение модели.
При решении задачи: «Бабушка приготовила 6 пирожков, а Лена на два пирожка меньше. Сколько всего пирожков они приготовили?» учащиеся составляют краткую запись, а затем преобразовывают ее в схематическую модель.
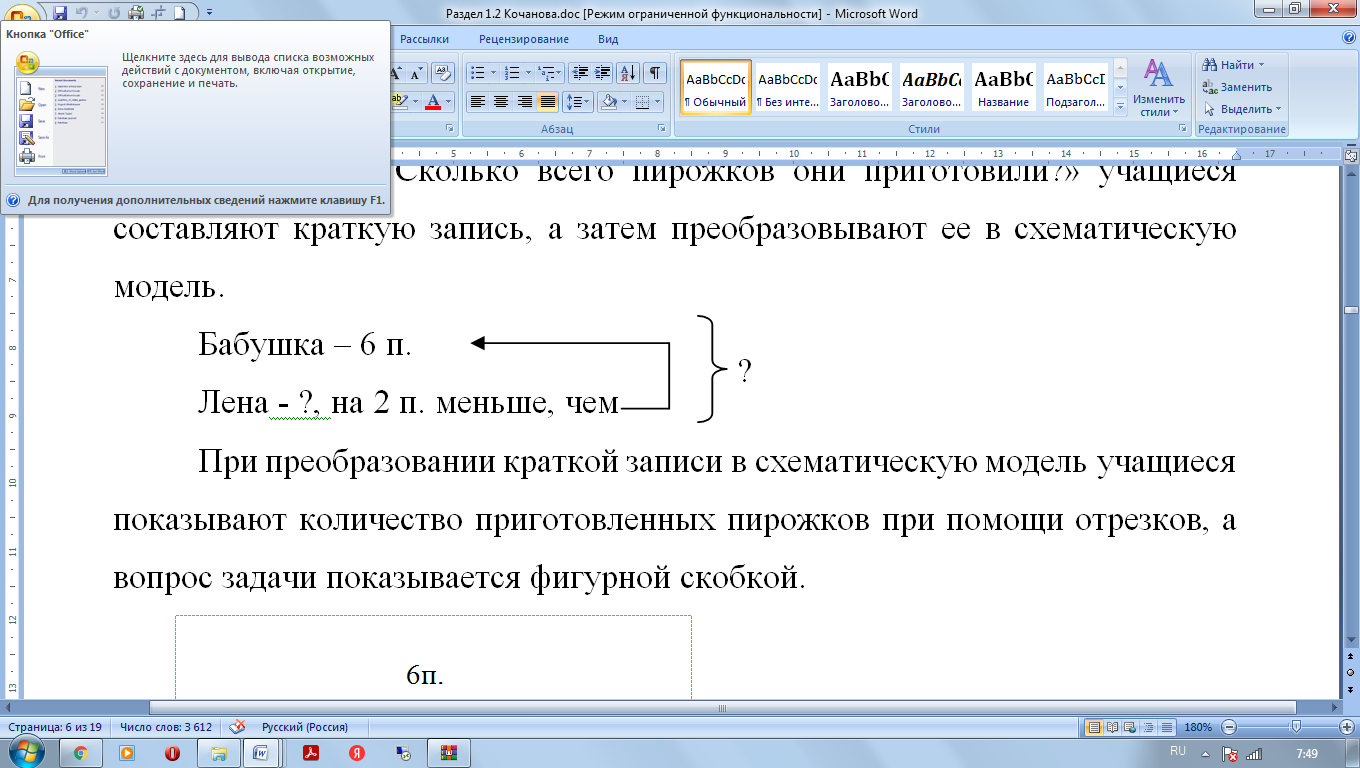
При преобразовании краткой записи в схематическую модель учащиеся показывают количество приготовленных пирожков при помощи отрезков, а вопрос задачи показывается фигурной скобкой.
Б. Л. |
4 шаг − усложнение модели.
Например, к задаче «На двух полках было 16 книг. На первой полке было 4 книги. Сколько книг на второй полке?» дается схема.
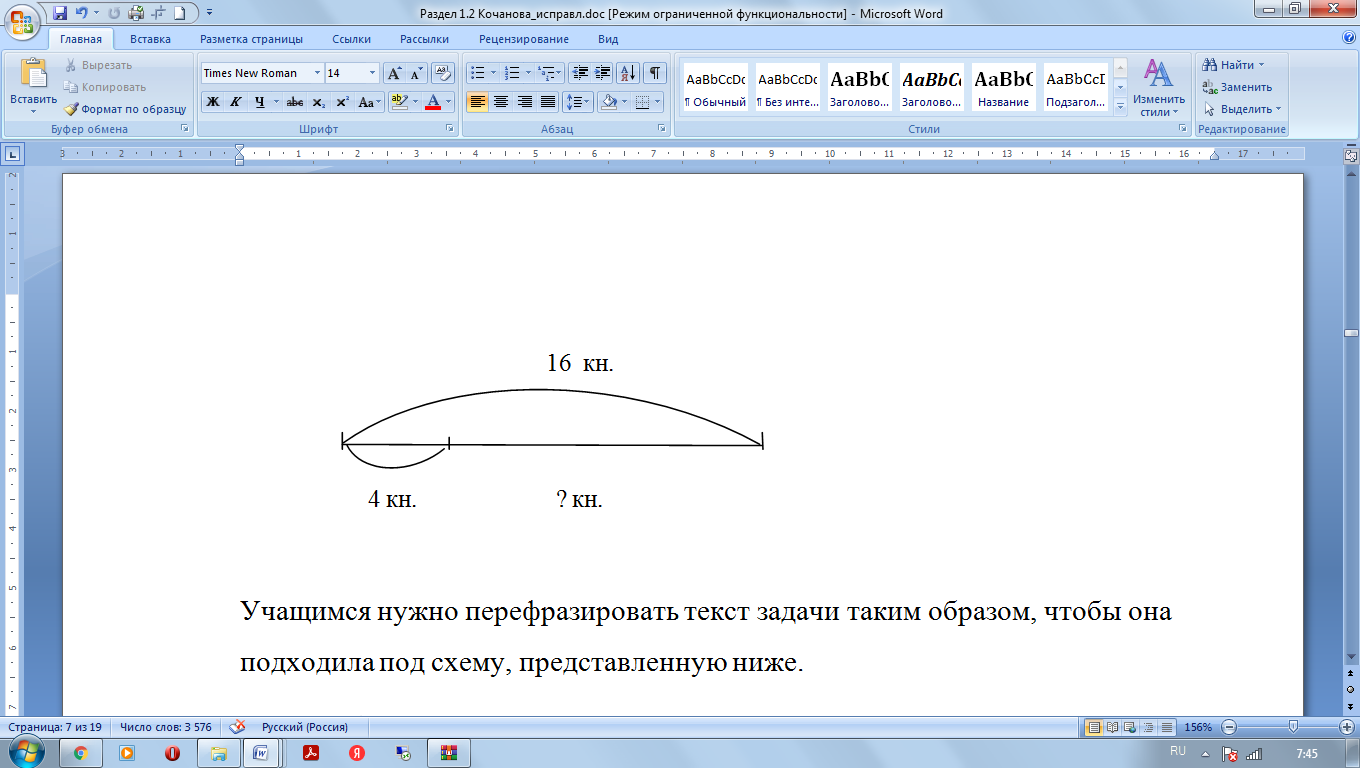
Учащимся нужно перефразировать текст задачи таким образом, чтобы она подходила под схему, представленную ниже.
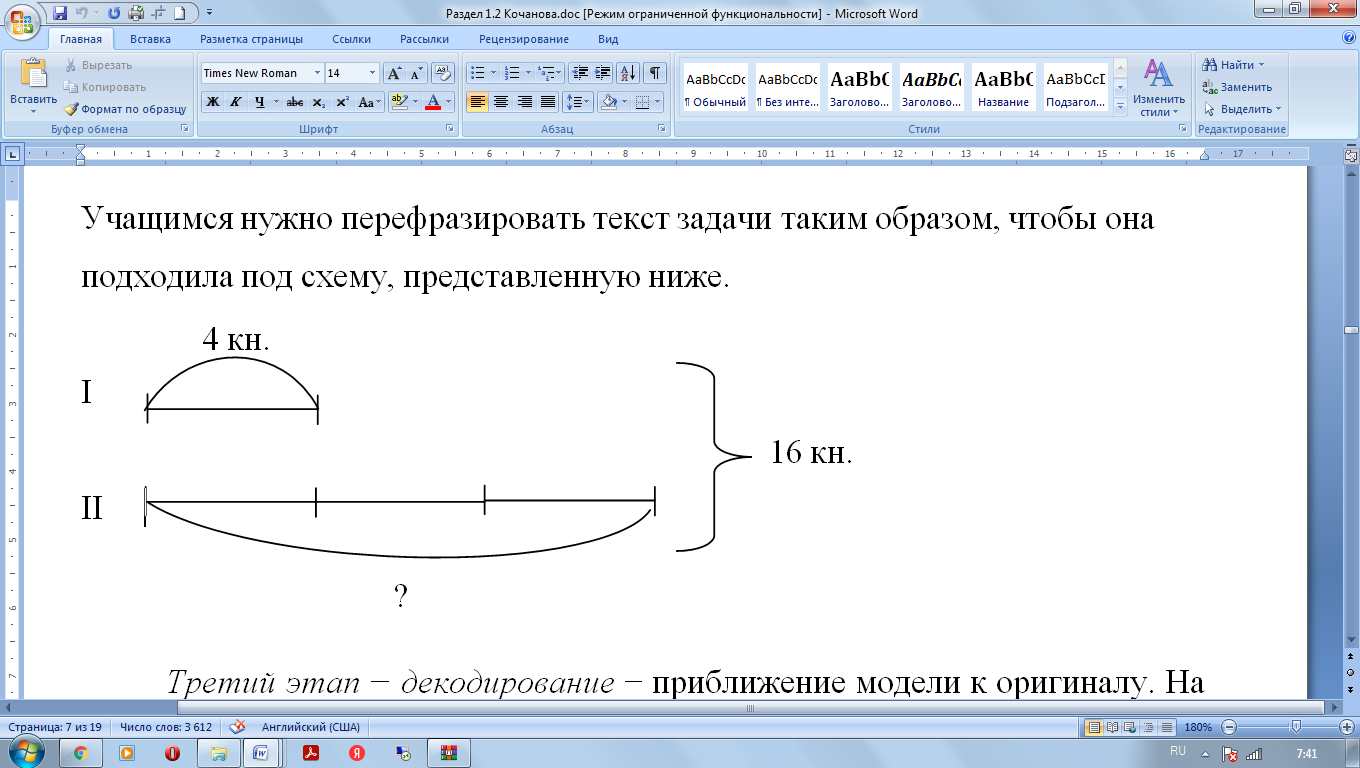
Третий этап − декодирование − приближение модели к оригиналу. На данном этапе используются такие приемы, как:
1) практическое применение модели;
2) использование моделей для описания реальных предметов и явлений;
3) соотнесение результатов моделирования с реальностью;
4) сравнение модели и оригинала.
Приведем пример: в наборе было 10 цветных карандашей. Для рисунка Оля использовала 4 из них. На сколько больше карандашей осталось неиспользованными, чем было использовано? Выберите модель, которая будет подходить к условию данной задачи.
Фаддейчева Т.И., Однораленко Е.А. в своей статье «Использование приема моделирования в процессе решения текстовых задач» отмечают, что результаты всероссийских проверочных работ свидетельствуют об актуальности проблемы формирования умений решать составные задачи. Одним из способов решения данной проблемы является использование моделей. Построение графической модели в некоторых случаях позволяет найти способ решения задачи, а также выявить новые связи и отношения между данными и искомыми и, соответственно, выбрать другие арифметические действия для решения задачи. Рассмотрим предложенные авторами статьи примеры работы с моделью при решении задач.
Задача. 3а класс собрал в два раза больше макулатуры, чем 3б класс. Когда 3а сдал 25 кг макулатуры, а 3б 5 кг, макулатуры у них осталось поровну. Сколько макулатуры собрали 3а и 3б классы в отдельности?
В процессе анализа текста задачи полезно построить базовую, исходную модель, опираясь на отношение: «3а класс собрал в два раза больше макулатуры, чем 3б класс». При построении модели сохраняются отношения
«больше», «меньше», «равно», поэтому отрезок, показывающий количество
макулатуры, собранной учащимися 3а класса в 2 раза больше отрезка, который показывает количество макулатуры, собранной учащимися 3б класса.
3а
3б
Построенную модель необходимо дополнить с учетом того, что макулатуру сдавали оба класса, но в разном количестве. Учащиеся 3б класса сдали 5 кг, учащиеся 3а класса 25 кг, после этого у учеников обоих классов осталось макулатуры поровну. Отметим небольшую часть на нижнем отрезке справа и проведем вертикальную черту до пересечения с верхним отрезком.
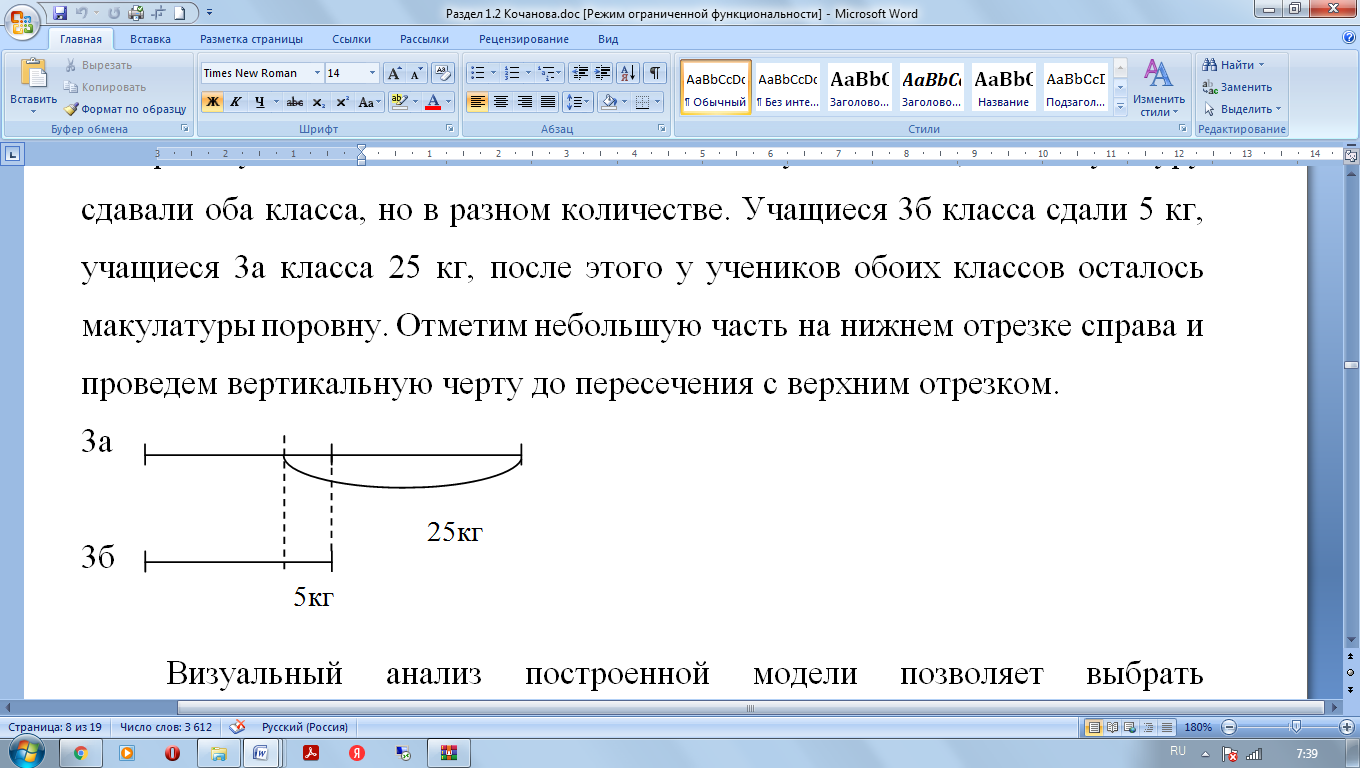
Визуальный анализ построенной модели позволяет выбрать арифметические действия для решения задачи. Разница между сданной макулатурой учащимися двух классов составляет одну часть или количество
макулатуры, собранной учащимися 3б класса.
Решение.
1) 25 – 5 = 20 (кг) - столько макулатуры собрали учащиеся 3б класса.
2) 20*2 = 40 (кг) - столько макулатуры собрали учащиеся 3а класса.
Ответ: 40 кг, 20 кг.
На примере задачи, рассмотренной выше, видим, что построение графической модели позволяет установить связи между объектами, описанными в тексте задачи и таким образом выбрать арифметические действия, необходимые для решения задачи. Анализ учебников по математике для начальной школы показывает, что учебные задания предполагают построение графической модели и решение задачи и лишь в некоторых случаях предлагается решить задачу двумя способами. В то же время в учебниках содержится довольно большое количество текстовых задач, которые можно решить тремя и более способами. Практика обучения математике в начальной школе свидетельствует о том, что поиску различных способов решения текстовых задач уделяется недостаточно внимания. Связано это с ограниченностью времени на уроке, а также дополнительной подготовкой учителя при разработке сценария урока. Тогда как выявление новых связей между данными и искомыми способствуют развитию логического, вариативного, нестандартного мышления.
Рассмотрим задачу.
Выставку книг посетили учащиеся 4 классов. В первый день 180 учеников, во второй день на 65 человек больше, чем в первый, а в третий день на 20 детей меньше, чем во второй день. Сколько всего учащихся посетили выставку книг за 3 дня?
Построим графическую модель ситуации, описанной в тексте задачи.
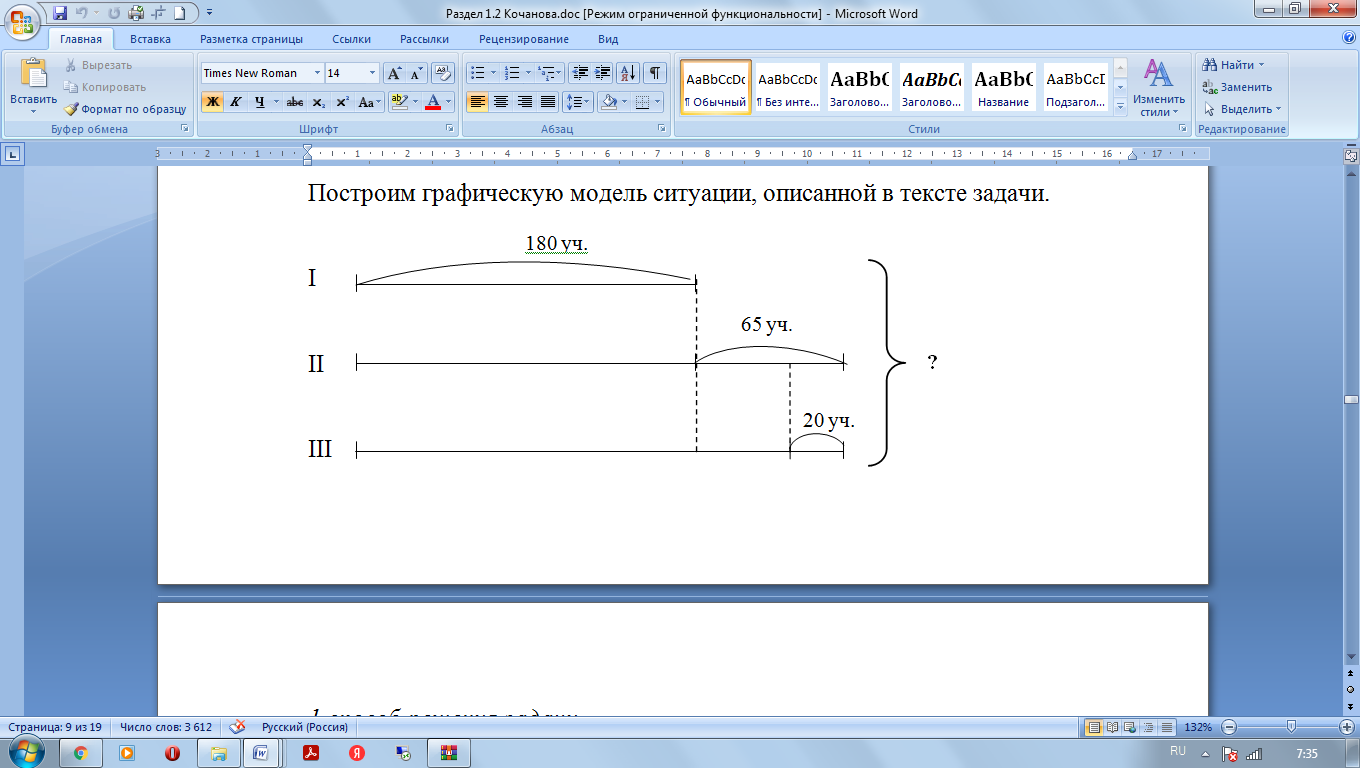
1 способ решения задачи.
1)180+65=245 (уч.) – столько учащихся посетило выставку во второй
день.
2)245-20=225 (уч.) - столько учащихся посетило выставку в третий день.
3) 180+245=425 (уч.) - столько учащихся посетило выставку в первый и второй день вместе.
4) 425+225=650 (уч.) - столько учащихся посетило выставку за три дня. Ответ: 650 учеников
Представленный способ решения задачи является стандартным: выбор арифметических действий и их последовательность полностью соответствует
связям и отношениям, представленным в тексте задачи.
Опишем другие способы решения, сочетая прием моделирования и предположения, не влияющего на конечный результат решения.
2 способ решения задачи.
1)180+65=245(уч.) – столько учащихся посетило выставку во второй день.
2)245+245=490(уч.) – столько учащихся посетило выставку во второй и третий день, если предположить, что в третий день посетило выставку столько учащихся, сколько во второй день.
3)490-20=470 (уч.) – столько учащихся посетило выставку во второй и третий день фактически.
4)470+180=650(уч.) - столько учащихся посетило выставку за три дня.
Ответ: 650 учеников.
3 способ решения задачи.
1)180*3=540(уч.) – столько учащихся посетило выставку книг, если бы во
второй и в третий дни выставку посетило столько детей, сколько в первый день.
2)65+65=130(уч.) – на столько больше посетило выставку фактически, если бы в третий посетили на 65 человек больше, чем в первый.
3)130-20=110(уч.) – на столько фактически больше было посетителей за три дня, чем предполагалось.
4)540+110=650(уч.) - столько учащихся посетило выставку за три дня фактически.
Ответ: 650 учеников.
4 способ решения задачи.
1)180*3=540 (уч.) – столько учащихся посетило выставку книг, если бы во второй и в третий дни выставку посетило столько детей, сколько в первый день.
2)65-20=45 (уч.) – на столько больше посетило детей в третий день, чем в первый.
3)65+45=110 (уч.) – на столько больше учащихся посетило выставку во второй и третий день, чем предполагалось.
4)540+110=650 (уч.) - столько учащихся посетило выставку за три дня фактически.
Ответ: 650 учеников
5 способ решения задачи.
1)180+65=245 (уч.) – столько учащихся посетило выставку во второй день.
2)245*3=735 (уч.) - столько учащихся посетило выставку книг, если бы в первый и в третий дни выставку посетило столько детей, сколько во второй день.
3)735-65=670 (уч.) - столько учащихся посетило выставку за три дня, учитывая, что фактически в первый день посетителей было на 65 человек меньше, чем во второй день.
4)670-20=650(уч.) - столько учащихся посетило выставку за три дня, учитывая, что фактически в третий день посетителей было на 20 человек меньше, чем во второй день.
Ответ: 650 учеников
Рассмотренные примеры показывают, что сочетание графического моделирования и других приемов способствует поиску различных способов решения задачи. При этом учащиеся выполняют операции анализа, сравнения, обобщения, таким образом происходит развитие мышления, в том числе таких его характеристик как логика, критичность, вариативность, обобщенность, отвлеченность.
Методику использования моделирования при организации творческой работы младших школьников по написанию математических сочинений, докладов (сообщений), сказок, которая начинается на уроке и продолжается в домашней работе, раскрывают в своей статье «Использование моделирования при обучении младших школьников математике» А.М. Черкасова, Н.В. Аммосова. Они подчеркивают, что работа по написанию математических сказок наиболее интересна детям, так как требует проявления их фантазии и воображения. Героями математических сказок могут быть геометрические фигуры, числа, знаки действий и т. д. В сказках дети могут описывать сказочные версии происхождения какого-либо математического понятия.
Написание математической сказки проходит по следующему плану:
1) выбор темы из предложенных учителем (если учитель предлагает несколько тем на выбор);
2) определение героев сказки в зависимости от темы;
3) создание сюжета сказки;
4) написание текста сказки;
5) представление сказки;
6) применение итога (результата) сказки.
Например, после знакомства второклассников с рулеткой длиной в 1 метр учитель предлагает детям написать сказку на тему «Как появилась рулетка». Написанию сказки предшествует работа в классе по актуализации знаний, необходимых для написания сказки. По просьбе учителя дети описывают рулетку словами (это полоска, на которой нанесены числа от 0 до 100 по порядку, расположенные на одинаковом расстоянии друг от друга) и зарисовывают ее в тетрадях, приняв за 1 дм две тетрадные клетки (по согласованию с учителем, так как нет возможности изобразить объект в тетради в натуральную величину), т. е. строится графическая модель рулетки в виде рисунка. Затем учитель предлагает детям вспомнить русскую народную сказку «Снегурочка». Дети по цепочке читают первую часть сказки из книги, предложенной учителем, в которой говорится о том, как старики лепили Снегурочку. Ведется беседа с детьми, в результате которой выясняется, что главный герой сказки – девочка Снегурочка, которую старики слепили из снега. Ученики рассказывают сюжет прочитанной части сказки и вспоминают, что в сказках всегда присутствует волшебство (слепили девочку из снега, и она ожила). Обращая внимание детей на сказку о рулетке, учитель спрашивает их, кто будет главным героем их сказки. Они отвечают, что главным героем их сказки будет Рулетка. Внимание детей обращается на сходство сюжетов (как появилась Снегурочка и как появилась рулетка – сделали люди из подходящих материалов). На вопрос, что нужно знать о рулетке, чтобы написать сказку о том, как она появилась, дети отвечают, что нужно знать то, что представляет собой рулетка, как она устроена.
Составляется инструкция по написанию сказки (алгоритмическая модель процесса создания сказки):
1) Вспомни, что такое рулетка;
2) Вспомни, какие объекты необходимы, чтобы можно было сделать рулетку;
3) Придумай сюжет своей сказки, используя элементы волшебства;
4) Составь 5–6 предложений и запиши их в тетрадь.
По составленной инструкции, т. е. используя алгоритмическую модель создания сказки, ребята дома сочиняют сказку. Дети предлагают множество различных сюжетов. Приведем пример одного из них: «Вдоль дороги тянулась длинная лента. И никто не знал ее длину. У дороги росло дерево. Вместо листьев на дереве росли числа. Их было очень много. Вдруг подул сильный ветер и сорвал с дерева все числа. Числа упали и разместились вдоль ленты по порядку возрастания, сначала однозначные, потом – двузначные, на одинаковом расстоянии друг от друга. Так появилась рулетка».
Сказки зачитываются детьми на уроке и с помощью учителя выявляются и исправляются недочеты, неточности. По итогам работы проводится конкурс на лучшую сказку, победители награждаются призами. Впоследствии проводится инсценировка лучшей сказки.
Организация такой взаимосвязи работы на уроке и домашней работы с использованием моделирования способствует усвоению детьми моделирования как универсального способа учебной деятельности, развитию умения смоделировать любую ситуацию, изучить ее с помощью модели и сделать соответствующие выводы.
Некоторые методические варианты применения моделей показаны в таблице на примере решения задачи: «У Пети три шара, у Оли – 2 шара. Сколько всего шаров у детей?»[11].
Методические варианты применения моделей
| № | Метод | Описание |
| Репродуктивно-наглядный | Учитель демонстрирует модель (на доске, наборном полотне) и на её основе даёт словесное объяснение о способе решения задачи. «Ребята, я располагаю на наборном полотне 3 кружка слева, потому что у нас в задаче сказано, что у Коли было 3 яблока, и 2 кружка справа - столько яблок, по условию задачи у Лены. В задаче нужно узнать, сколько всего яблок у детей, поэтому я придвину кружки друг к другу. Значит, эта задача решается с помощью действия сложения. Давайте запишем вместе решение задачи: 3+2=5». | |
| Продуктивно-наглядный | Учитель демонстрирует модель (на доске, на наборном полотне) и в процессе её построения проводит с детьми беседу эвристического характера с тем, чтобы дети сами «открыли» способ решения задачи. «Дети, сейчас я покажу слева яблоки Коли, а справа яблоки Лены. Сколько кружков я должна поставить слева? Почему? (После ответов детей учитель располагает на наборном полотне 3 кружка слева.) Сколько кружков нужно расположить на наборном полотне справа? Почему? (После ответов детей учитель располагает на наборном полотне 2 кружка справа.) Что нужно сделать, чтобы показать, что мы собираем вместе яблоки Коли и Лены? ( После ответов детей учитель придвигает одни кружки к другим). Каким действием решается задача? Почему? Как запишем решение задачи?» | |
| Репродуктивно-практический | Учитель строит модель ( на доске, на наборном полотне) и одновременно просит детей построить такую же модель на парте или в тетради. В ходе построения модели учитель даёт словесное объяснение репродуктивного характера о способе решения задачи. «Дети, сейчас я на наборном полотне поставлю 3 кружка слева, потому что, по условию задачи, у Коли было 3 яблока, а 2 кружка справа – столько яблок у Лены. Положите вместе со мной 3 кружка на парте слева, а 2 кружка на парте справа. В задаче нужно узнать, сколько всего яблок у детей. Поэтому я придвину кружки друг к другу и вы тоже на партах придвиньте свои кружки друг к другу. Так как мы с вами придвигаем кружки, задача решается сложением. Давайте запишем вместе решение задачи: 3+2=5». | |
| Продуктивно-практический | Учитель строит модель (на доске, наборном полотне) и одновременно просит детей построить такую же модель на парте или в тетради. В процессе построения модели учитель проводит с детьми беседу эвристического характера с тем, чтобы дети сами «открыли» способ решения задачи. «Дети, давайте покажем слева яблоки Коли, а справа яблоки Лены. Сколько кружков мы должны показать слева? Почему? Давайте вместе сделаем это: я поставлю кружки слева на наборном полотне, а вы положите их слева у себя на парте. Сколько кружков мы должны показать справа? Почему? Давайте вместе сделаем это: я поставлю кружки справа на наборном полотне, а вы положите их справа у себя на парте. Что нужно сделать, чтобы показать, что мы собираем вместе яблоки Коли и Лены? Правильно, нужно придвинуть кружки друг к другу. Давайте вместе сделаем это: я на наборном полотне, а вы у себя на партах. Что мы сделали, чтобы найти ответ к задаче? Значит, каким действием решается задача? Как запишем решение задачи?» |
При объяснении трудного для детей материала рекомендуется использовать продуктивно-практический вариант моделирования, поскольку при этом обеспечивается эвристическая форма передачи информации («субъективное открытие знания») и практическая деятельность ребёнка по построению и преобразованию моделей, что особенно важно для ребёнка со средними или слабыми математическими способностями.
Для педагога моделирование это инструмент построения учебного процесса, а для ученика это универсальный инструмент основного вида деятельности – обучения. В процессе моделирования у учащихся формируются основные учебные умения, определяющие развитие психологических способностей личности, осуществляющиеся в рамках нормативно-возрастного развития личностной и познавательной сфер ребенка.
Дата добавления: 2022-02-05; просмотров: 475;











