Нахождение оригинала по изображению
В общем случае нахождение оригинала по изображению достигается использованием теоремы обращения:
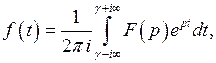
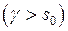 . (1)
. (1)
Однако для произвольных 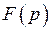 это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения
это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения 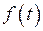 в предположении, что
в предположении, что 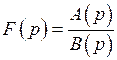 отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе. Разложив
отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе. Разложив 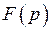 на простейшие дроби, получим
на простейшие дроби, получим
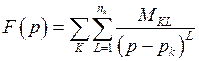 ,
,
где 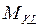 – комплексные числа,
– комплексные числа, 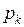 – нули знаменателя
– нули знаменателя 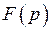 ,
, 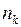 – их порядок. Пользуясь формулой 10 таблицы соответствия и теоремой линейности, легко получить
– их порядок. Пользуясь формулой 10 таблицы соответствия и теоремой линейности, легко получить
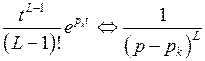 и
и 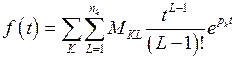 .
.
Часто бывает удобнее разложить изображение на простейшие дроби вида
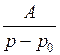 ,
, 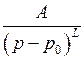 ,
,  .
.
При этом также можно использовать формулы таблицы соответствия.
Пример 1. 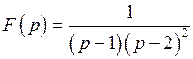 .Найти
.Найти 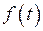 .
.
Решение. Разложим дробь 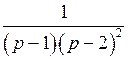 на простейшие дроби:
на простейшие дроби:
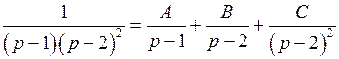 ,
,
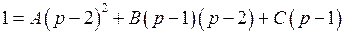 .
.
Полагая 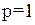 , получим
, получим 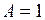 , при
, при 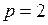 , получим
, получим 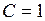 , при
, при 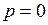 , имеем
, имеем  .
.
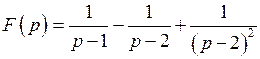 .
.
Используя теорему линейности и таблицу соответствия (формулы 2,10), получим
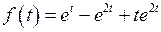 .
.
При нахождении 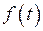 по
по 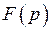 иногда целесообразно использовать теорему о произведении изображений (теорему о свертке).
иногда целесообразно использовать теорему о произведении изображений (теорему о свертке).
Пример 2. 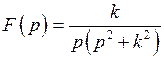 .Найти
.Найти 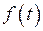 .
.
Решение
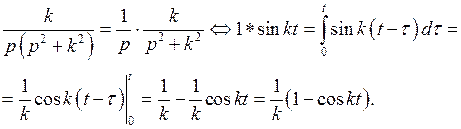
В некоторых случаях удобно использовать формулу Дюамеля.
Пример 3. 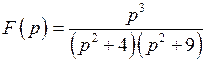 .Найти
.Найти 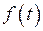 .
.
Решение. 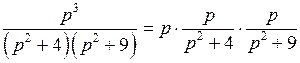 ;
;
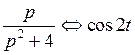 ;
; 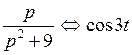 .
.
По формуле Дюамеля имеем
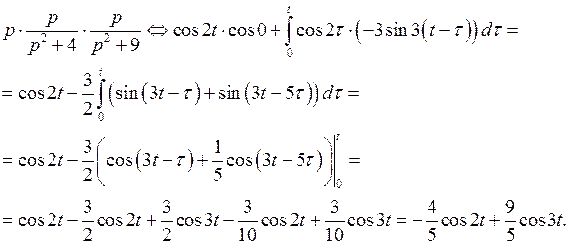
Можно находить 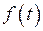 по
по 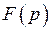 , используя теорию вычетов (теорему разложения, которая выводится из (1)). А именно: если
, используя теорию вычетов (теорему разложения, которая выводится из (1)). А именно: если 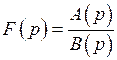 отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе, то
отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе, то
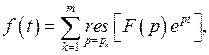 (2)
(2)
где 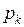 – полюса функции
– полюса функции 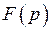 .
.
Пример 4. 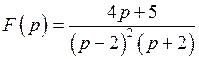 .Найти оригинал.
.Найти оригинал.
Решение. Функция 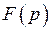 имеет два полюса:
имеет два полюса: 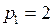 – полюс второго порядка и
– полюс второго порядка и 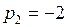 – полюс первого порядка. По формуле (2)
– полюс первого порядка. По формуле (2)
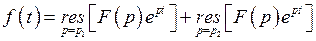 .
.
Находим вычеты: 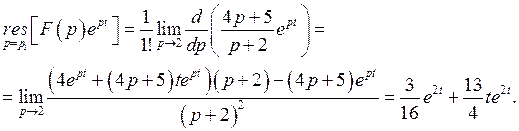
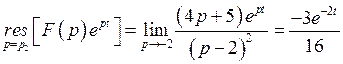 .
.
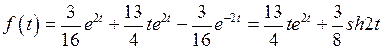 .
.
Если все полюса 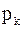 функции
функции 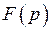 первого порядка,
первого порядка, 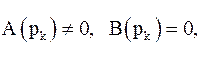
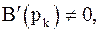
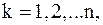 то формула
то формула 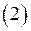 принимает вид
принимает вид
 ,
,
где сумма берется по всем корням 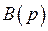 .
.
Дата добавления: 2022-05-27; просмотров: 234;











