Преобразование Лапласа и его свойства
Функцией – оригиналом будем называть любую комплекснозначную функцию 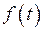 действительного аргумента
действительного аргумента 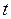 , удовлетворяющую следующим условиям:
, удовлетворяющую следующим условиям:

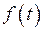 непрерывна вместе со своими производными достаточно высокого порядка на всей оси
непрерывна вместе со своими производными достаточно высокого порядка на всей оси 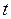 , кроме отдельных точек, в которых
, кроме отдельных точек, в которых 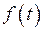 или ее производные терпят разрыв I-го рода, причем на каждом конечном интервале оси
или ее производные терпят разрыв I-го рода, причем на каждом конечном интервале оси 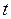 таких точек имеется лишь конечное число;
таких точек имеется лишь конечное число;
 для всех отрицательных
для всех отрицательных 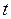
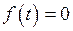 ;
;

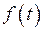 возрастает не быстрее показательной функции, то есть существуют такие постоянные
возрастает не быстрее показательной функции, то есть существуют такие постоянные 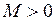 ,
, 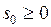 , что для всех
, что для всех 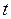
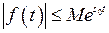 . Наименьшее число
. Наименьшее число 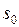 , для которого выполняется это неравенство, назовем показателем роста
, для которого выполняется это неравенство, назовем показателем роста 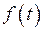 ; для ограниченных оригиналов можно, очевидно, принять
; для ограниченных оригиналов можно, очевидно, принять 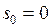 .
.
Простейшей функцией – оригиналом является так называемая единичная функция или функция Хэвисайда
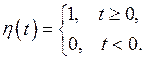
Очевидно, умножение функции 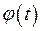 на
на 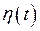 «гасит» эту функцию для
«гасит» эту функцию для 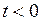 и оставляет без изменения для
и оставляет без изменения для 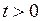 . Если функция
. Если функция 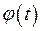 удовлетворяет условиям 1 и 3 и не удовлетворяет условию 2, то произведение
удовлетворяет условиям 1 и 3 и не удовлетворяет условию 2, то произведение
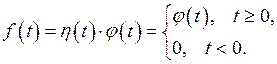
будет удовлетворять и условию 2, то есть будет оригиналом (например, 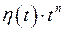 ,
, 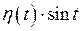 ,
, 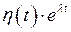 и т.д.). Для простоты записи будем, как правило, опускать множитель
и т.д.). Для простоты записи будем, как правило, опускать множитель 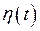 , условившись, что все функции, которые будем рассматривать, равны нулю для всех отрицательных
, условившись, что все функции, которые будем рассматривать, равны нулю для всех отрицательных 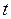 . Например, вместо
. Например, вместо 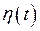 будем писать 1, вместо
будем писать 1, вместо 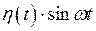 – просто
– просто 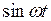 и так далее.
и так далее.
Изображением функции 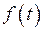 (по Лапласу) или преобразованием Лапласафункции
(по Лапласу) или преобразованием Лапласафункции 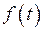 называют функцию комплексного переменного
называют функцию комплексного переменного 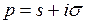 , определяемую соотношением
, определяемую соотношением 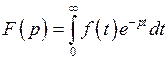 . Связь оригинала и изображения будем записывать так:
. Связь оригинала и изображения будем записывать так:
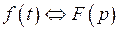 .
.
Дата добавления: 2022-05-27; просмотров: 146;











