Применение вычетов к вычислению интегралов
Основная теорема Коши. Пусть 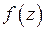 – аналитическая функция в ограниченной односвязной области
– аналитическая функция в ограниченной односвязной области 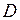 , за исключением конечного числа изолированных особых точек
, за исключением конечного числа изолированных особых точек 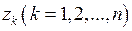 , и пусть замкнутая кривая
, и пусть замкнутая кривая 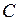 , охватывающая эти особые точки, целиком лежит в области
, охватывающая эти особые точки, целиком лежит в области 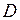 . Тогда если кривая
. Тогда если кривая 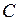 ориентирована в положительном направлении, то
ориентирована в положительном направлении, то
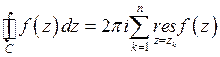 .
.
Пример 1. Вычислить 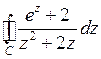 , где
, где 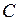 – окружность
– окружность 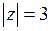 .
.
Решение. Подынтегральная функция 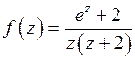 имеет два полюса I–го порядка
имеет два полюса I–го порядка 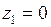 и
и 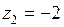 , которые расположены внутри круга
, которые расположены внутри круга 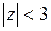 . Согласно теореме Коши, получаем
. Согласно теореме Коши, получаем
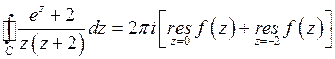 .
.
Найдем вычеты:
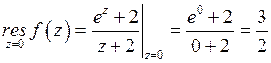 ,
,
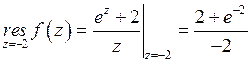 .
.
Итак, 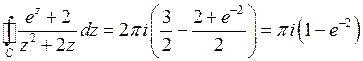 .
.
Пример 2. Вычислить 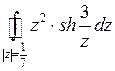 .
.
Решение.Подынтегральная функция 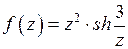 имеет изолированную особую точку
имеет изолированную особую точку 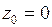 внутри круга
внутри круга 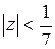 . Для определения характера изолированной особой точки разложим функцию
. Для определения характера изолированной особой точки разложим функцию 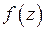 в ряд Лорана в кольце
в ряд Лорана в кольце 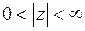 . Воспользуемся разложением функции
. Воспользуемся разложением функции 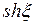 в ряд Тейлора:
в ряд Тейлора:
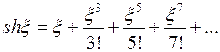 и положим
и положим 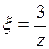 :
:
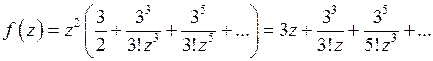 .
.
В силу единственности разложения в ряд Лорана, полученное разложение функции 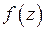 по степеням
по степеням 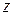 является рядом Лорана для данной функции в кольце
является рядом Лорана для данной функции в кольце 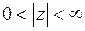 . Так как главная часть этого ряда Лорана содержит бесконечное множество слагаемых, то точка
. Так как главная часть этого ряда Лорана содержит бесконечное множество слагаемых, то точка 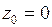 является существенно особой точкой
является существенно особой точкой 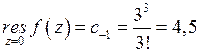 .
.
Согласно теореме Коши получаем
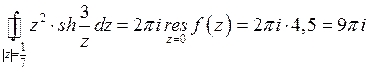 .
.
Пример 3. Вычислить 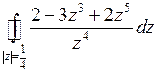 .
.
Решение.Подынтегральная функция 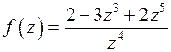 имеет изолированную особую точку
имеет изолированную особую точку 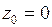 внутри круга
внутри круга 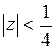 . Так как
. Так как 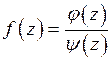 , где
, где 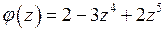 , причем
, причем 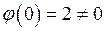 , а
, а 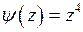 , то
, то 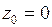 есть полюс 4-го порядка.
есть полюс 4-го порядка.
Следовательно,
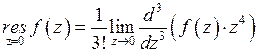 =
= 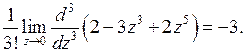
Согласно теореме Коши получаем
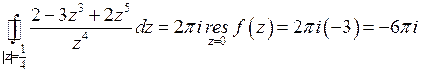 .
.
Пример 4. Вычислить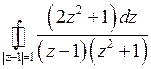 .
.
Решение.Функция 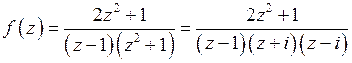 имеет полюсы I–го порядка в точках
имеет полюсы I–го порядка в точках 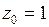 ,
, 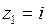 ,
, 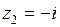 . Точки
. Точки 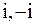 находятся вне круга
находятся вне круга 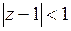 , так как
, так как 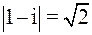 >1,
>1, 
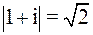 >1. Внутри круга
>1. Внутри круга 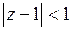 находится один полюс
находится один полюс 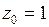 первого порядка. Найдем
первого порядка. Найдем 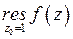 по формуле (2)
по формуле (2) 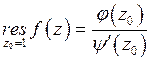 , где
, где 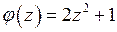 ,
, 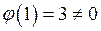 и
и 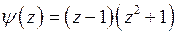 ,
, 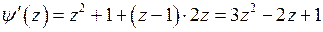 ,
, 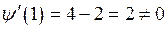 . Имеем,
. Имеем, 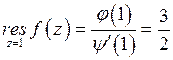 .
.
Следовательно, по теореме Коши:
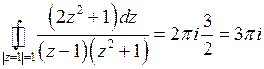 .
.
Интеграл вида 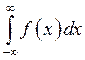
Теорема 1.Пусть 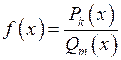 , где
, где 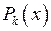 и
и 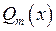 – многочлены степеней
– многочлены степеней 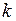 и
и 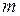 соответственно. Если
соответственно. Если 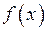 непрерывна на всей действительной оси и
непрерывна на всей действительной оси и 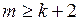 , то
, то
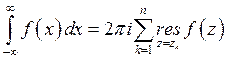 ,
,
где 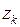 – полюса функции
– полюса функции 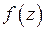 в верхней полуплоскости.
в верхней полуплоскости.
Пример 1.Вычислить 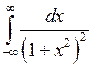 .
.
Решение.Так как 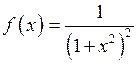 , то
, то 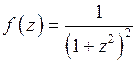 удовлетворяет условию теоремы 1. Функция
удовлетворяет условию теоремы 1. Функция 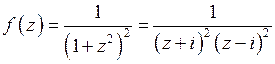 имеет полюс
имеет полюс 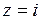 второго порядка в верхней полуплоскости. Поэтому, согласно теореме 1, находим
второго порядка в верхней полуплоскости. Поэтому, согласно теореме 1, находим
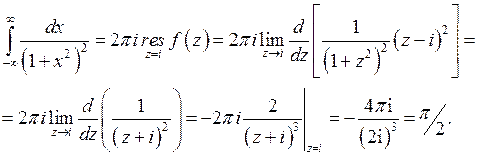
Интеграл вида 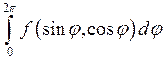
Интегралы вида 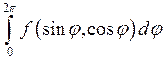 , где
, где 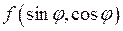 – рациональная функция от
– рациональная функция от 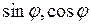 , сводятся к интегралам по замкнутому контуру от функций комплексного переменного. Для этого выражаем синус и косинус по формулам Эйлера и делаем замену
, сводятся к интегралам по замкнутому контуру от функций комплексного переменного. Для этого выражаем синус и косинус по формулам Эйлера и делаем замену 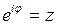 .
.
Имеем 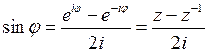 ,
, 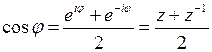 .
.
Подставляя эти выражения в подынтегральную функцию, получим 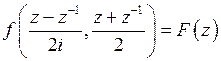 – рациональную функцию. Логарифмируя
– рациональную функцию. Логарифмируя
равенство 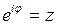 , находим
, находим 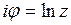 и
и 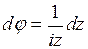 . При изменении
. При изменении 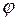 от 0 до
от 0 до 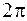 точка
точка 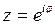 пробегает единичную окружность
пробегает единичную окружность 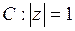 в положительном направлении.
в положительном направлении.
Следовательно, 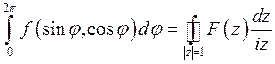 .
.
Последний интеграл по замкнутому контуру можно вычислить с помощью основной теоремы Коши.
Пример 2.Вычислить 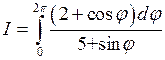 .
.
Решение. Пусть 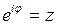 , тогда
, тогда
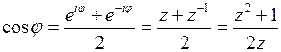 ,
, 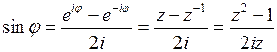 ,
,
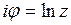 ,
, 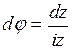 ; При изменении
; При изменении 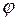 от 0 до
от 0 до 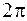 точка
точка 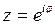 пробегает единичную окружность
пробегает единичную окружность 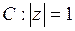 в положительном направлении.
в положительном направлении.
Следовательно,
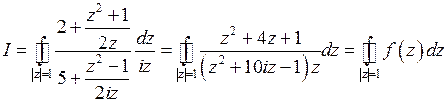 ,
,
где 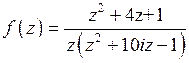 .
.
Для нахождения полюсов 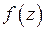 найдем нули знаменателя и их порядки.
найдем нули знаменателя и их порядки. 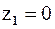 – ноль первого порядка.
– ноль первого порядка.
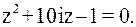
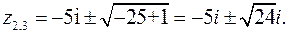
Так как 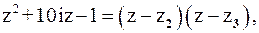 то
то 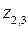
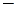 также нули первого порядка. Поскольку числитель функции
также нули первого порядка. Поскольку числитель функции 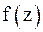 отличен от нуля в этих точках, то подынтегральная функция имеет три полюса первого порядка:
отличен от нуля в этих точках, то подынтегральная функция имеет три полюса первого порядка:
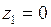 ,
, 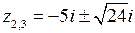 ,
,
При этом 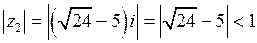 ,
,
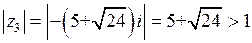 .
.
Итак, внутри единичной окружности 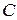 находятся два полюса первого порядка:
находятся два полюса первого порядка:
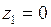 и
и 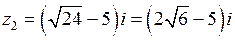 .
.
Найдем вычеты по формуле (2):
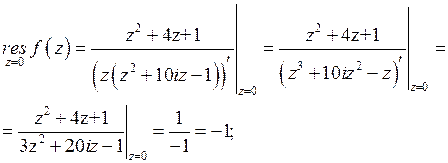
аналогично,
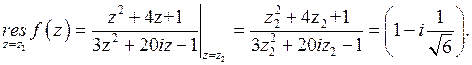
Итак, 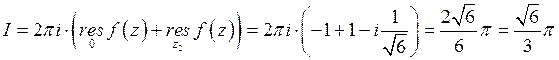 .
.
Интегралы вида 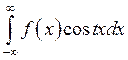 ,
, 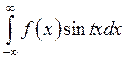
Теорема 2.Пусть 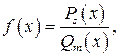 где
где 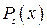 и
и 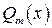 – многочлены степеней
– многочлены степеней 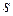 и
и 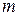 соответственно. Если
соответственно. Если 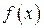 непрерывна на всей действительной оси и
непрерывна на всей действительной оси и 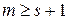 , то при
, то при 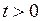
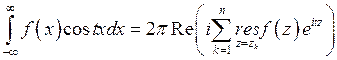 ,
,
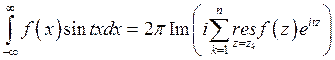 ,
,
где 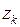 – полюса функции
– полюса функции 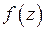 в верхней полуплоскости,
в верхней полуплоскости, 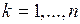 .
.
Пример 1. Вычислить 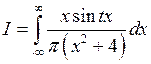 .
.
Решение.По условию, 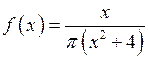 , значит
, значит 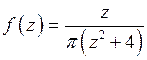 . Функция
. Функция 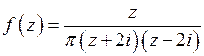 имеет полюс первого порядка
имеет полюс первого порядка 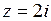 в верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (1) получаем
в верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (1) получаем
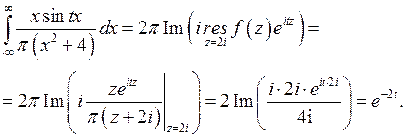
Пример 2.Вычислить 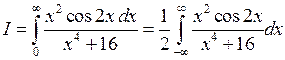 .
.
Решение.По условию 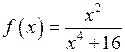 и
и 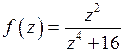 .
.
Функция 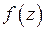 удовлетворяет условиям теоремы 2. Найдем полюса
удовлетворяет условиям теоремы 2. Найдем полюса 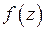 в верхней полуплоскости:
в верхней полуплоскости:
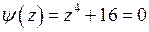 ,
, 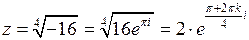 ,
, 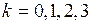 ;
;
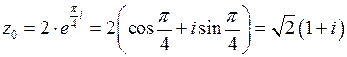 ,
, 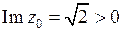 ;
;
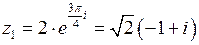 ,
, 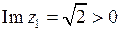 ;
;
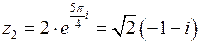 ,
, 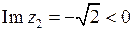 ;
;
 ,
, 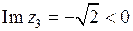 .
.
Так как 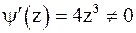 в точках
в точках 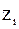 , то
, то 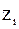 – нули первого порядка функции
– нули первого порядка функции 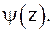 Кроме того
Кроме того 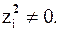 Следовательно функция
Следовательно функция 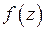 имеет полюсы первого порядка
имеет полюсы первого порядка 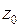 ,
, 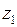 в верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (2)
в верхней полуплоскости. Поэтому на основании теоремы 2 и формулы (2)
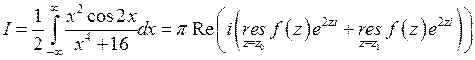 ,
,
где 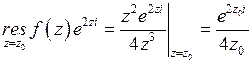 ,
, 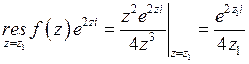 .
.
Имеем:
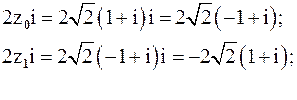
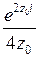
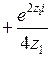
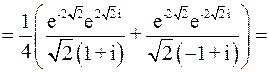
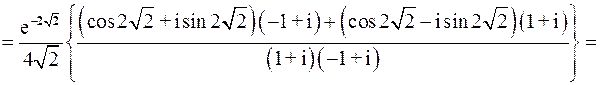
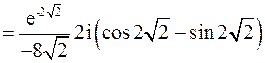 .
.
Следовательно,
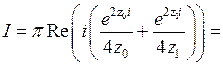
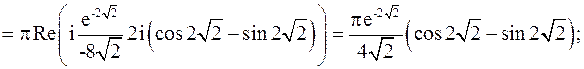
Дата добавления: 2022-05-27; просмотров: 266;











