По теореме о дифференцировании оригинала имеем
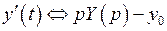 ,
,  .
.
Применяя к обеим частям уравнения преобразование Лапласа, получим алгебраическое уравнение
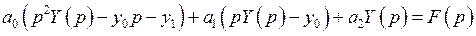 , или
, или
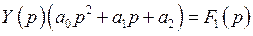 ,
, 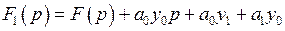 .
.
Отсюда
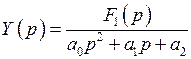 .
.
Переходя от этого изображения к оригиналу, получим искомую функцию 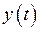 .
.
Пример 1. Найти частное решение дифференциального уравнения 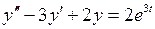 ,
, 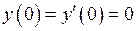 .
.
Решение. Пусть 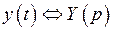 ;
; 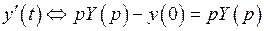 ;
;
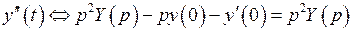 ;
; 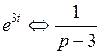 .
.
Запишем операторное уравнение:
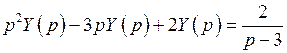 .
.
Откуда
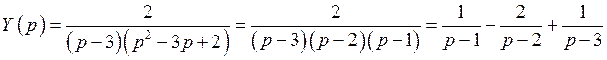 .
.
Используя теорему линейности и таблицу соответствия формула (2), получим
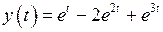 .
.
Пример 2. Найти частное решение дифференциального уравнения 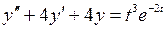 ,
, 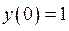 ,
, 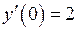 .
.
Решение. 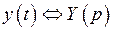 ;
; 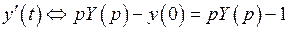 .
.
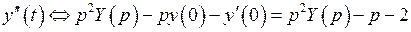
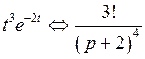 ;
; 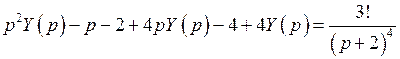 ;
;
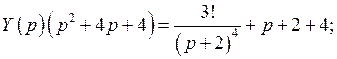
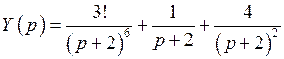 .
.
Используя таблицу соответствия формула (10) и теорему линейности, получим
 .
.
Отметим особую роль формулы Дюамеля при решении линейных дифференциальных уравнений с постоянными коэффициентами. Пусть требуется решить линейное дифференциальное уравнение с постоянными коэффициентами
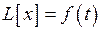 (3)
(3)
при нулевых начальных условиях. Если известно решение 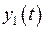 уравнения
уравнения
 (4)
(4)
с той же левой частью, а правой частью, равной 1, при нулевых начальных условиях, то формула Дюамеля позволяет записать решение данного уравнения без всяких вычислений. В самом деле пусть 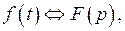
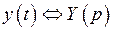 ,
, 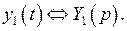
Тогда операторные уравнения, соответствующие уравнениям (3), (4), имеют вид
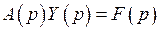 ,
, 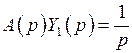 ,
,
откуда 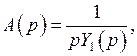
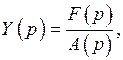
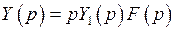 .
.
Тогда, согласно формуле Дюамеля,
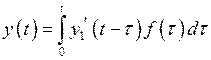 или
или 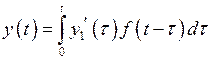 ,
,
или 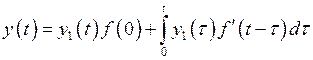 ,
,
или  .
.
Пример 3.Найти решениедифференциального уравнения с нулевыми начальными условиями, 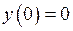 ,
, 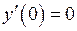 .
.
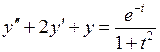 .
.
Решение. Решаем сначала уравнение 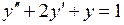 с теми же начальными условиями операционным методом:
с теми же начальными условиями операционным методом:
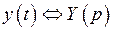 ,
, 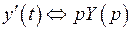 ;
; 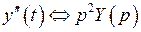 ;
; 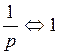 ;
;
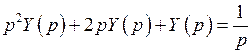 ;
;
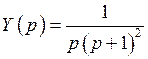 разложим на простейшие дроби:
разложим на простейшие дроби:
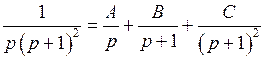 ;
;
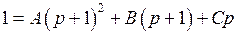 ;
;
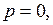
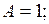
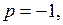
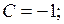
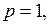
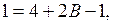
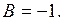
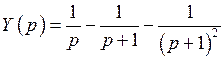 .
.
Используя теорему линейности и формулы соответствия, получим
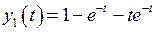 ,
, 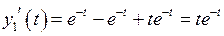 .
.
Применяя формулу Дюамеля, имеем
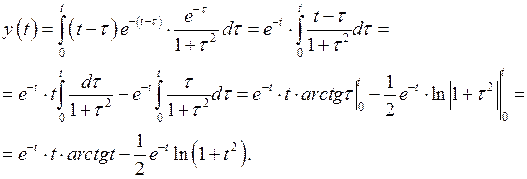
Дата добавления: 2022-05-27; просмотров: 186;











