Умножение изображений
Если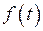 
и 
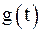являются оригиналам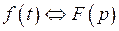и, 
и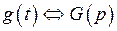 
, то выражению 
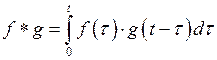, называемому сверткой функци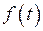й и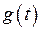 
, соответствует произведение изображений, то есть 
.
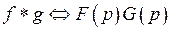Существенное значение имеет так называемые формулы Дюамеля:
.
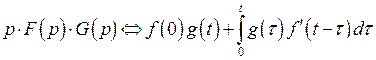
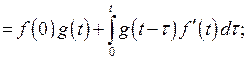
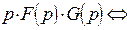
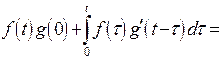
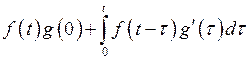При нахождении изображений по оригиналам и оригиналов по изображениям, удобно пользоваться формулами соответствия, которые приведены в следующей таблице:
| Номер формулы | Оригинал | Изображение |
| ||
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
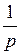
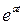
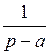
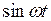
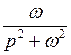
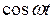
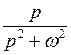
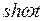
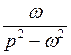
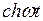
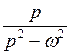
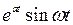
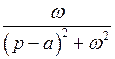
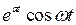
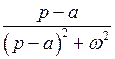
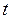
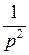
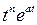
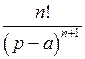
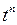
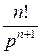
7.2. Нахождение изображения по оригиналу
Задачу о нахождении изображения по оригиналу можно решать, используя таблицу соответствия и свойства преобразования Лапласа.
Пример 1.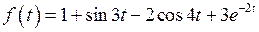 
. Найти 
.
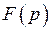Решение. Используя теорему линейности и формулы (1-4) таблицы соответствия, получим
.
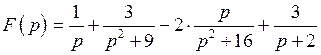Пример 2.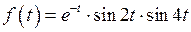 
. Найти .
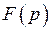Решение.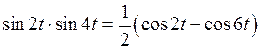 
.
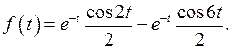
Используя теорему линейности, теорему затухания и формулу (8) таблицы соответствия, получим
.
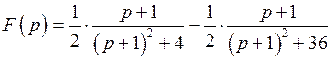Пример 3.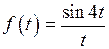 
. Найти .
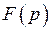Решение.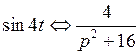 
.
Используя теорему об интегрировании изображения, находим
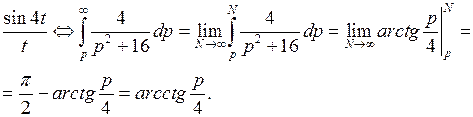
Пример 4.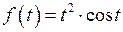 
. Найти .
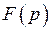Решение.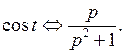 
Используя теорему о дифференцировании изображения, находим
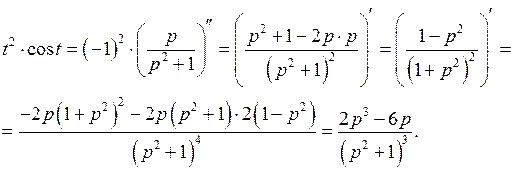
Если функция 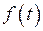задана разными выражениями на разных промежутках, то ее надо предварительно представить в ви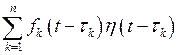де 
, где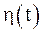 
– функция Хэвисайда, а затем воспользоваться теоремой запаздывания.
Пример 5.Найти изображение функции
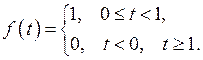
Решение.Представим 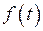в виде 
.
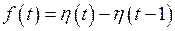Имеем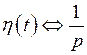 
; 
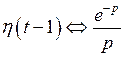. Используя свойство линейности, получим 
.
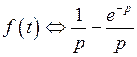Пример 6.Найти 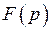, если оригинал 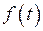задан графиком:
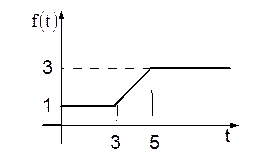
Решение
В аналитической форме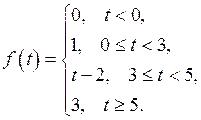 
Заметим, что на интервале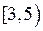 
уравнение прямой найдено по формуле
.
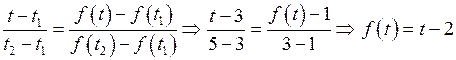Рассмотрим функции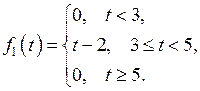 
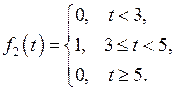
Тогда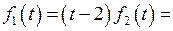 
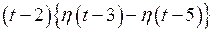(см. пример 5).
Поступая аналогично, получим
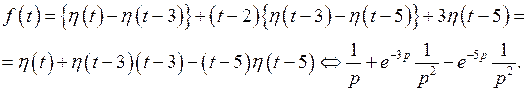
Дата добавления: 2022-05-27; просмотров: 182;
Поиск по сайту
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по географии
Публикации по медицине
