Теорема аналитичности
Для всякого оригинала 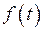 изображение
изображение 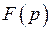 определено в полуплоскости
определено в полуплоскости 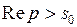 , где
, где 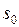 – показатель роста
– показатель роста 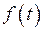 , и является в этой полуплоскости аналитической функцией. Если точка
, и является в этой полуплоскости аналитической функцией. Если точка 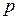 стремится к бесконечности так, что
стремится к бесконечности так, что 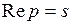 неограниченно возрастает, то
неограниченно возрастает, то 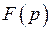 стремится к нулю:
стремится к нулю: 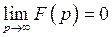 .
.
Предельные соотношения
Если 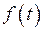 является оригиналом вместе со своей производной
является оригиналом вместе со своей производной 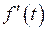 и
и 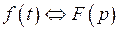 , то
, то 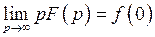 , где
, где 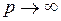 внутри угла
внутри угла 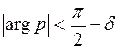 , и
, и 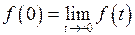 ; если существует
; если существует 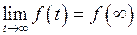 , то
, то 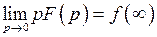 .
.
Теорема линейности
Если 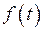 и
и 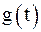 являются оригиналами и
являются оригиналами и 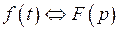 ,
, 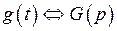 , то для любых комплексных постоянных
, то для любых комплексных постоянных 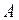 и
и 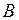
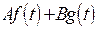 также является оригиналом и
также является оригиналом и 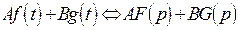 , то есть линейной комбинации оригиналов соответствует линейная комбинация изображений.
, то есть линейной комбинации оригиналов соответствует линейная комбинация изображений.
Теорема подобия
Если 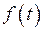 является оригиналом и
является оригиналом и 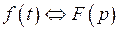 , то для любого постоянного
, то для любого постоянного 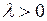 функция
функция 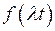 также является оригиналом и
также является оригиналом и 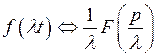 , то есть умножение аргумента оригинала на положительное число
, то есть умножение аргумента оригинала на положительное число 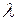 приводит к делению аргумента изображения и самого изображения
приводит к делению аргумента изображения и самого изображения 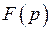 на то же число
на то же число 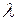 .
.
Теорема смещения
Если 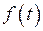 является оригиналом и
является оригиналом и 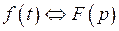 , то для любого действительного или комплексного числа
, то для любого действительного или комплексного числа 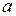
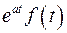 также является оригиналом и
также является оригиналом и 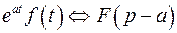 , то есть умножение оригинала на функцию
, то есть умножение оригинала на функцию 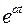 влечет за собой «смещение» независимой переменой
влечет за собой «смещение» независимой переменой 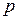 .
.
Дата добавления: 2022-05-27; просмотров: 161;











