Метод припасовывания
Этот метод применяется для случая, когда нелинейная характеристика 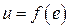 в САУ рис. 2.2 представляется в виде кусочно-линейной, т.е. на отдельных участках изменения переменной
в САУ рис. 2.2 представляется в виде кусочно-линейной, т.е. на отдельных участках изменения переменной 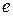 нелинейная характеристика аппроксимируется линейной зависимостью. Теоретически этот подход можно применять для систем любого порядка при вычислении как свободных (
нелинейная характеристика аппроксимируется линейной зависимостью. Теоретически этот подход можно применять для систем любого порядка при вычислении как свободных ( 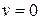 ), так и вынужденных процессов (
), так и вынужденных процессов ( 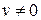 ).
).
Основная идея подхода следующая. Диапазон изменения переменной 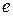 на входе нелинейности разбивается на ряд интервалов, так что в
на входе нелинейности разбивается на ряд интервалов, так что в 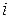 -ом интервале
-ом интервале 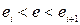 нелинейная функция
нелинейная функция 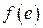 заменяется линейной
заменяется линейной 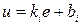 . Тогда в
. Тогда в 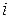 -ом интервале уравнения (2.6), (2.8) или (2.9) становятся линейными и теоретически можно найти общее решение соответствующих линейных дифференциальных уравнений при заданном входе
-ом интервале уравнения (2.6), (2.8) или (2.9) становятся линейными и теоретически можно найти общее решение соответствующих линейных дифференциальных уравнений при заданном входе 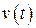 :
:
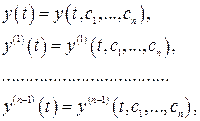 (2.30)
(2.30)
где 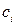 – произвольные постоянные.
– произвольные постоянные.
Задавая начальные условия для частного (конкретного решения) 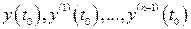 при условии
при условии 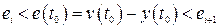 и полагая в (2.30)
и полагая в (2.30) 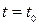 , находим произвольные постоянные и соответствующие частные решения
, находим произвольные постоянные и соответствующие частные решения 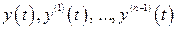 , которые справедливы только при
, которые справедливы только при 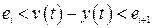 .
.
Далее находим значение момента времени 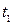 , при котором
, при котором 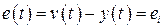 , либо
, либо 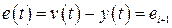 . При
. При 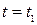 по выражениям (2.30) вычисляем конечные значения решения и его производных
по выражениям (2.30) вычисляем конечные значения решения и его производных 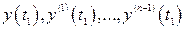 , которые принимаем за начальные значения решения в следующем
, которые принимаем за начальные значения решения в следующем 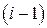 или
или 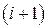 интервалах. Далее процесс поинтервального решения повторяется.
интервалах. Далее процесс поинтервального решения повторяется.
Итак, для каждого 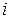 -го интервала изменения переменных системы имеем свою линейную модель, которая дает определенное решение, справедливое только для
-го интервала изменения переменных системы имеем свою линейную модель, которая дает определенное решение, справедливое только для 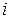 -го интервала. На границах интервалов, там, где
-го интервала. На границах интервалов, там, где 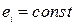 , производится припасовывание (склеивание, сшивание) решений: конечные значения решений для
, производится припасовывание (склеивание, сшивание) решений: конечные значения решений для 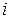 -го интервала становятся начальными значениями искомого решения для следующего интервала. Отсюда и название метода – метод припасовывания решений. Фактически он уже применялся для нахождения решений дифференциальных уравнений для фазовых траекторий в пункте 2.3.3. Границы интервалов
-го интервала становятся начальными значениями искомого решения для следующего интервала. Отсюда и название метода – метод припасовывания решений. Фактически он уже применялся для нахождения решений дифференциальных уравнений для фазовых траекторий в пункте 2.3.3. Границы интервалов 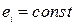 являются линиями переключения.
являются линиями переключения.
Пример 2.3. Пусть в нелинейной системе рис. 2.2 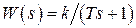 , а нелинейность имеет вид рис. 2.4, а, которая описывается уравнением
, а нелинейность имеет вид рис. 2.4, а, которая описывается уравнением
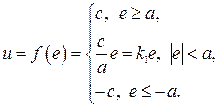 (2.31)
(2.31)
Исходная система нелинейных уравнений будет иметь вид
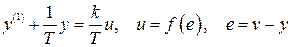 . (2.32)
. (2.32)
Исследуем процессы в системе при входном сигнале 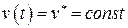 . Тогда из (2.32) с учетом (2.31) получим три модели системы для трех интервалов:
. Тогда из (2.32) с учетом (2.31) получим три модели системы для трех интервалов:
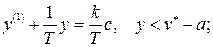
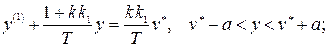
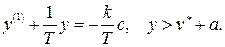
Общее решение в каждом случае будет иметь вид:
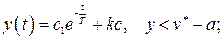
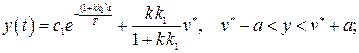 (2.33)
(2.33)
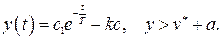
Пусть 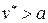 ,
, 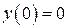 , тогда из первого уравнения (2.33) найдем
, тогда из первого уравнения (2.33) найдем 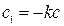 и решение будет
и решение будет 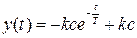 . Найдем момент времени
. Найдем момент времени 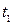 , когда
, когда 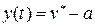 . Это вытекает из решения уравнения
. Это вытекает из решения уравнения 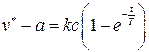 при условии
при условии 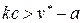 . Момент
. Момент 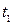 определится по формуле
определится по формуле
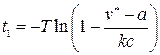 .
.
По первой формуле (2.33) определяем
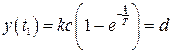 .
.
Конечное значение процесса 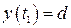 принимаем за начальное для второй формулы (2.33), тогда получим
принимаем за начальное для второй формулы (2.33), тогда получим 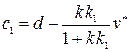 и
и
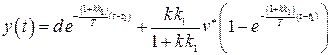 . (2.34)
. (2.34)
Итак, закон изменения координаты 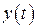 при
при 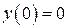 и
и 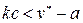
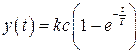 ,
, 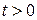 . (2.35)
. (2.35)
Если же 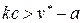 , то при
, то при 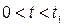 выход будет изменяться по закону (2.35), а далее при
выход будет изменяться по закону (2.35), а далее при 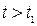 закон изменения будет (2.34).
закон изменения будет (2.34).
При 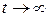 в первом случае на выходе имеем установившееся значение
в первом случае на выходе имеем установившееся значение 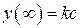 , а во втором
, а во втором 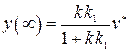 .
.
Дата добавления: 2022-02-05; просмотров: 704;











