Изолированные особые точки
Точка 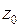 называется изолированной особой точкой функции
называется изолированной особой точкой функции 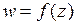 , если
, если 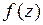 аналитична в кольце
аналитична в кольце 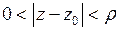 , но не определена в точке
, но не определена в точке 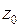
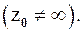
Если 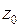 – изолированная особая точка функции
– изолированная особая точка функции 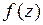 , то эту функцию можно разложить в ряд Лорана (3), который сходится к ней в кольце
, то эту функцию можно разложить в ряд Лорана (3), который сходится к ней в кольце 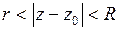 , где
, где 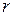 – сколь угодно малое положительное число, а
– сколь угодно малое положительное число, а 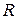 – расстояние от точки
– расстояние от точки 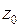 до другой особой точки функции
до другой особой точки функции 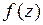 .
.
Изолированная особая точка 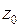 называется устранимой, если разложение (3) не содержит степеней разности
называется устранимой, если разложение (3) не содержит степеней разности 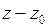 с отрицательными показателями, то есть
с отрицательными показателями, то есть
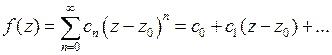 .
.
Точка 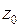 является устранимой особой точкой функции
является устранимой особой точкой функции 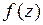 в том и только том случае, если функция
в том и только том случае, если функция 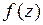 ограничена в некоторой окрестности точки
ограничена в некоторой окрестности точки 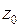 .
.
Пример 1.Функция 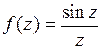 имеет изолированную особую точку
имеет изолированную особую точку 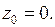 Чтобы найти разложение в ряд Лорана
Чтобы найти разложение в ряд Лорана 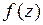 в окрестности точки
в окрестности точки 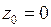 , воспользуемся формулой (5).
, воспользуемся формулой (5).
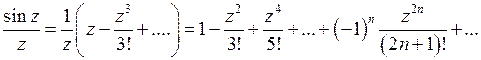 .
.
Это разложение не содержит степеней 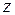 с отрицательными показателями. Следовательно, точка
с отрицательными показателями. Следовательно, точка 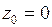 – устранимая особая точка.
– устранимая особая точка.
Изолированная особая точка 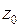 называется полюсом, если разложение (3) содержит конечное число
называется полюсом, если разложение (3) содержит конечное число 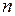 степеней разности
степеней разности 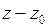 с отрицательными показателями, при этом число
с отрицательными показателями, при этом число 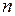 называется порядком полюса.
называется порядком полюса.
Для определения порядка полюса функции 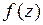 можно использовать теорему.
можно использовать теорему.
Для того, чтобы точка 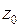 являлась полюсом порядка
являлась полюсом порядка 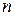 функции
функции 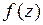 , необходимо и достаточно, чтобы функцию
, необходимо и достаточно, чтобы функцию 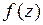 можно было представить в виде
можно было представить в виде
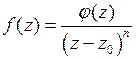 , (7)
, (7)
где 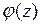 – аналитическая функция в окрестности точки
– аналитическая функция в окрестности точки 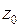 и
и 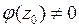 .
.
Полюса и нули аналитических функций связаны друг с другом.
Нулём функции 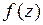 называют любую точку
называют любую точку 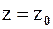 , в которой
, в которой 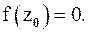 Разлагая аналитическую функцию в ряд Тейлора (1) в окрестности нуля, получим:
Разлагая аналитическую функцию в ряд Тейлора (1) в окрестности нуля, получим:
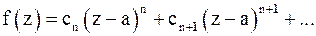 , (8)
, (8)
где 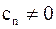 и
и 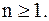 Число n называют порядком нуля аналитической функции
Число n называют порядком нуля аналитической функции 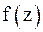 в точке
в точке 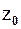 . Из (8) следует, что в окрестности нуля порядка n аналитическая функция
. Из (8) следует, что в окрестности нуля порядка n аналитическая функция 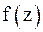 допускает представление
допускает представление
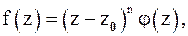 (9)
(9)
где 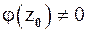 . Кроме того, порядок нуля можно определить следующим образом.
. Кроме того, порядок нуля можно определить следующим образом.
Если 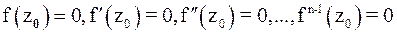 , а
, а 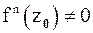 , то порядок нуля аналитической функции
, то порядок нуля аналитической функции 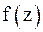 в точке
в точке 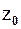 равен n.
равен n.
Справедливо утверждение.
Если аналитическую функцию 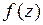 можно представить в виде
можно представить в виде 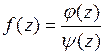 , где аналитические функции
, где аналитические функции 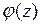 и
и 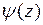 имеют в точке
имеют в точке 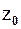 нули порядка k и m соответственно,
нули порядка k и m соответственно, 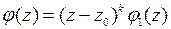 и
и 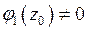 ,
, 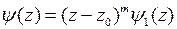 и
и 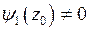 ,то в точке
,то в точке 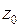 функция
функция 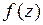 имеет полюс порядка
имеет полюс порядка 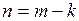 , при
, при 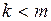 ; устранимую особую точку при
; устранимую особую точку при 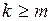 .
.
В частности, если 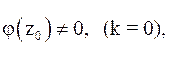 а
а 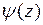 имеет в этой точке нуль порядка
имеет в этой точке нуль порядка 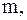 то
то 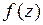 имеет в точке
имеет в точке 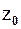 полюс порядка
полюс порядка 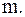 То есть в этом случае порядок полюса функции
То есть в этом случае порядок полюса функции 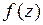 совпадает с порядком нуля знаменателя.
совпадает с порядком нуля знаменателя.
Изолированная особая точка 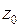 называется существенно особой, если разложение (3) содержит бесконечное множество степеней
называется существенно особой, если разложение (3) содержит бесконечное множество степеней 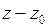 с отрицательными показателями.
с отрицательными показателями.
Пример 2.Найти все особые точки функций 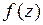 , определить их тип.
, определить их тип.
1. 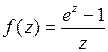 . 2.
. 2. 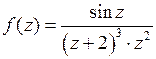 . 3.
. 3. 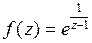 .
.
4. 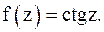
Решение.1. Чтобы найти разложение в ряд Лорана функции 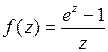 в окрестности точки
в окрестности точки 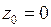 , воспользуемся формулой (5). Получим:
, воспользуемся формулой (5). Получим:
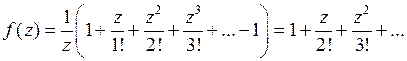 ,
,
Так как полученный ряд не содержит степеней 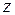 с отрицательными показателями, то точка
с отрицательными показателями, то точка 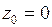 является устранимой особой точкой.
является устранимой особой точкой.
2. Функция 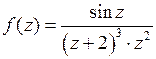 имеет две изолированные особые точки
имеет две изолированные особые точки 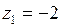 и
и 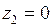 . Определим их тип. Пусть
. Определим их тип. Пусть 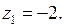 Представим функцию в виде
Представим функцию в виде 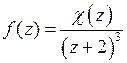 , где
, где 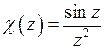 ,
, 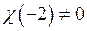 .
.
Тогда, согласно (7), 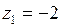 есть полюс порядка
есть полюс порядка 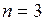 .
.
Пусть 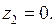 Представим функцию
Представим функцию 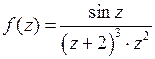 в виде
в виде 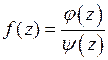 , где
, где 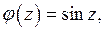
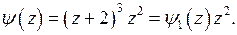 Так как
Так как 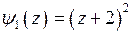 при
при 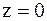 ,
, 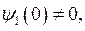 то порядок нуля знаменателя
то порядок нуля знаменателя 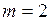 .
.
Для  имеем:
имеем: 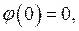
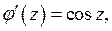
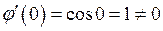 , откуда следует, что
, откуда следует, что 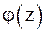 имеет ноль первого порядка, то есть
имеет ноль первого порядка, то есть 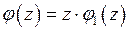 и
и 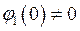 .
.
Следовательно, точка 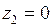 есть полюс порядка
есть полюс порядка 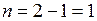 , то есть простой полюс.
, то есть простой полюс.
3. Функция 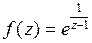 имеет изолированную особую точку
имеет изолированную особую точку 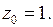 Подставим в разложение в ряд Тейлора (5) функции
Подставим в разложение в ряд Тейлора (5) функции 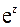 вместо z выражение
вместо z выражение 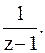 Получим разложение
Получим разложение 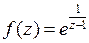 в окрестности особой точки
в окрестности особой точки 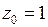
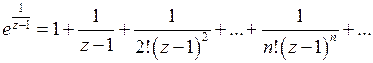 .
.
Этот ряд содержит бесконечное множество степеней 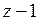 с отрицательными показателями; следовательно,
с отрицательными показателями; следовательно, 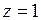 – существенно особая точка.
– существенно особая точка.
4. Для функции 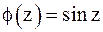 точки
точки 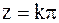 (k – целое число) являются нулями первого порядка, так как
(k – целое число) являются нулями первого порядка, так как 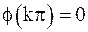 ,
, 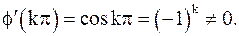 Тогда для
Тогда для 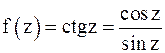 точки
точки 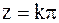 являются полюсами первого порядка (см. (7)), так как
являются полюсами первого порядка (см. (7)), так как 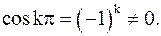
Бесконечно удаленную точку 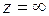 называют изолированной особой точкой функции
называют изолированной особой точкой функции 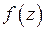 , если в некоторой ее окрестности (то есть вне круга с центром в точке
, если в некоторой ее окрестности (то есть вне круга с центром в точке 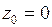 достаточно большого радиуса) нет других особых точек функции
достаточно большого радиуса) нет других особых точек функции 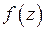 . Для изучения поведения функции
. Для изучения поведения функции 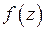 в окрестности точки
в окрестности точки 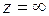 полагают
полагают 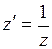 . Тогда окрестность точки
. Тогда окрестность точки 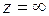 перейдет в окрестность точки
перейдет в окрестность точки 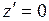 и
и 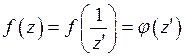 . Если
. Если 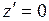 является устранимой, полюсом или существенно особой точкой для функции
является устранимой, полюсом или существенно особой точкой для функции 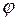 , то
, то 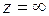 считают, соответственно, устранимой, полюсом или существенно особой точкой функции
считают, соответственно, устранимой, полюсом или существенно особой точкой функции 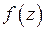 .
.
Можно показать, что точка 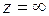 будет устранимой, полюсом или существенно особой точкой функции
будет устранимой, полюсом или существенно особой точкой функции 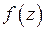 , если ряд Лорана для
, если ряд Лорана для 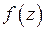 в этой точки окрестности не содержит степеней
в этой точки окрестности не содержит степеней 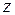 с положительными показателями, содержит их в конечном числе или бесконечное множество соответственно.
с положительными показателями, содержит их в конечном числе или бесконечное множество соответственно.
Пример 3.Исследовать поведение функции 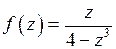 в окрестности бесконечно удаленной точки.
в окрестности бесконечно удаленной точки.
Решение.Введем переменную 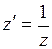 . Тогда
. Тогда
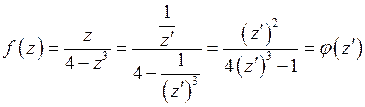 .
.
Так как 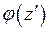 ограничена в окрестности точки
ограничена в окрестности точки 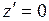 ,
, 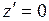 является устранимой особой точкой для
является устранимой особой точкой для 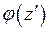 , то и точка
, то и точка 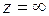 также является устранимой особой точкой для функции
также является устранимой особой точкой для функции 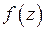 .
.
Пример 4. Исследовать поведение функции 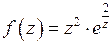 в окрестности бесконечно удаленной точки.
в окрестности бесконечно удаленной точки.
Решение. Разложим данную функцию в ряд Лорана. Для этого подставим в разложение в ряд Тейлора (5) функции 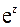 вместо z выражение
вместо z выражение 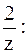
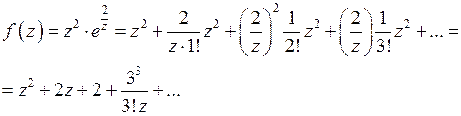
Это разложение содержит конечное число степеней 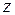 с положительными показателями, причем наивысший показатель степени
с положительными показателями, причем наивысший показатель степени 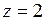 . Поэтому точка
. Поэтому точка 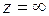 является полюсом второго порядка для функции
является полюсом второго порядка для функции 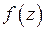 .
.
Дата добавления: 2022-05-27; просмотров: 222;











