Интегрирование функций комплексного переменного
Пусть заданы функция комплексного переменного 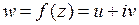 и кусочно-гладкая кривая
и кусочно-гладкая кривая 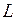 . Последнее означает, что L состоит из конечного числа гладких дуг (дуг с непрерывно изменяющейся касательной). Если кривая L задана параметрическими уравнениями
. Последнее означает, что L состоит из конечного числа гладких дуг (дуг с непрерывно изменяющейся касательной). Если кривая L задана параметрическими уравнениями
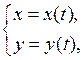 (1)
(1)
где 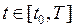 , то кривую L будем всегда считать ориентированной в направлении возрастания параметра t.
, то кривую L будем всегда считать ориентированной в направлении возрастания параметра t.
Интеграл от функции 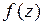 можно определить через криволинейные интегралы от действительных функций
можно определить через криволинейные интегралы от действительных функций 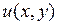 и
и 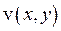 следующим образом:
следующим образом:
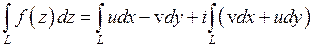 . (2)
. (2)
Пример 1.Вычислить интеграл 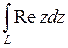 , где
, где 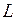 – отрезок прямой, соединяющей точки
– отрезок прямой, соединяющей точки 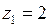 и
и 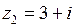 .
.
Решение.У нас 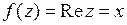 ,
, 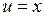 ,
, 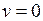 и, согласно (2), получим
и, согласно (2), получим
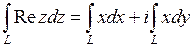 .
.
Так как прямая проходит через точки 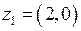 и
и 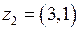 комплексной плоскости, то ее уравнение имеет вид
комплексной плоскости, то ее уравнение имеет вид 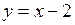 ,
, 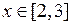 .
.
Поэтому окончательно находим
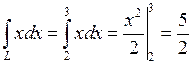 ,
,
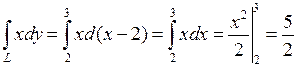 ,
,
Таким образом, 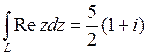 .
.
Если кривая задана параметрическими уравнениями
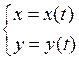 , где
, где 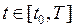 , то переменная
, то переменная 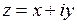 примет вид:
примет вид:
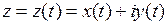 ;
; 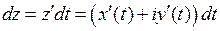 .
.
В этом случае
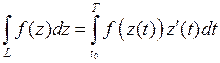 . (3)
. (3)
То есть для вычисления 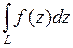 надо в подынтегральном выражении заменить
надо в подынтегральном выражении заменить 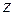 на
на 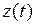 как под знаком функции, так и под знаком дифференциала и вычислить определенный интеграл в пределах от
как под знаком функции, так и под знаком дифференциала и вычислить определенный интеграл в пределах от 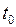 до
до 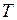 .
.
Пример 2.Вычислить 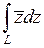 ,
,
где 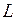 – отрезок параболы
– отрезок параболы 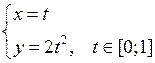
Решение.По условию 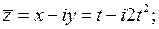
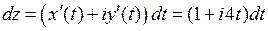 .
.
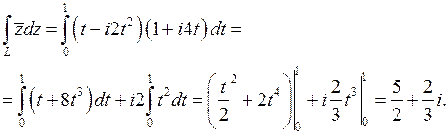
Если кривая 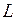 является окружностью с центром в точке
является окружностью с центром в точке 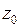 и радиусом
и радиусом 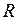 , то
, то 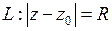 (см. пример 1 из п.2.1). Запишем комплексное число
(см. пример 1 из п.2.1). Запишем комплексное число 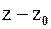 в показательной форме
в показательной форме 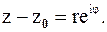 Для всех точек окружности
Для всех точек окружности 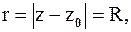
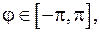 откуда следует, что
откуда следует, что 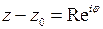 , или
, или 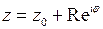 ,
, 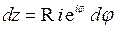 ,
, 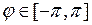 . Тогда
. Тогда
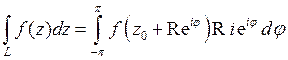 . (4)
. (4)
Формулы (2) – (4) используются чаще всего в том случае, если подынтегральная функция 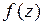 не является аналитической в области, содержащей кривую
не является аналитической в области, содержащей кривую 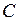 .
.
Если функция 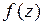 аналитическая в односвязной области, содержащей кривую
аналитическая в односвязной области, содержащей кривую 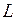 , то
, то
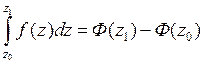 , где
, где 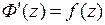 .
.
Пример 3.Вычислить интеграл 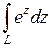 , где
, где 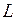 – отрезок прямой, содержащей точки
– отрезок прямой, содержащей точки 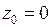 и
и 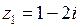 .
.
Решение.Функция 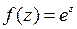 является аналитической на плоскости
является аналитической на плоскости 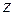 . Поэтому
. Поэтому
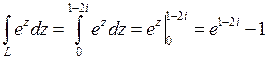 .
.
Ряды
Ряд Тейлора
Справедливы следующие теоремы.
1. Всякую функцию 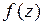 , аналитическую в круге с центром в точке
, аналитическую в круге с центром в точке 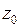 можно представить внутри этого круга в виде суммы ряда Тейлора:
можно представить внутри этого круга в виде суммы ряда Тейлора:

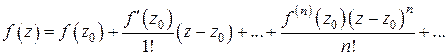 (1)
(1)
Во всякой замкнутой области, принадлежащей этому кругу, ряд Тейлора (1) сходится равномерно.
2. Всякую аналитическую функцию в каждой внутренней точке области аналитичности можно разложить в ряд Тейлора (1). Это разложение справедливо в области 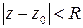 , где
, где 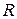 – расстояние от точки
– расстояние от точки 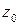 до ближайшей особой точки функции
до ближайшей особой точки функции 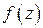 , то есть точки, в которой
, то есть точки, в которой 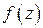 не является аналитической.
не является аналитической.
3. Если функция 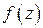 разлагается в окрестности точки
разлагается в окрестности точки 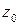 в степенной ряд
в степенной ряд 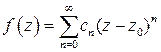 , то этот ряд является ее рядом Тейлора, то есть
, то этот ряд является ее рядом Тейлора, то есть
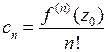 ,
, 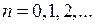 .
.
Пользуясь теоремой 3, можно разложить данную функцию 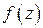 в ряд по степеням
в ряд по степеням 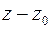 , который является ее рядом Тейлора в окрестности точки
, который является ее рядом Тейлора в окрестности точки 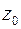 . Часто коэффициенты такого ряда находят, используя известные разложения функций
. Часто коэффициенты такого ряда находят, используя известные разложения функций 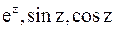 и т.д.
и т.д.
Напомним также разложение
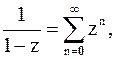 (2)
(2)
сходящееся в круге 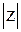 <1.
<1.
Пример 1.Разложить функцию 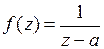 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 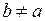 . Указать область, в которой справедливо это разложение.
. Указать область, в которой справедливо это разложение.
Решение.В окрестности точки 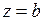 функция
функция 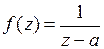 является аналитической. Следовательно, согласно теореме 2, ее можно разложить в ряд Тейлора. Для разложения в ряд Тейлора преобразуем данную функцию к виду
является аналитической. Следовательно, согласно теореме 2, ее можно разложить в ряд Тейлора. Для разложения в ряд Тейлора преобразуем данную функцию к виду
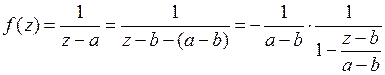 .
.
Разложим второй сомножитель в ряд по формуле (2). Область сходимости этого ряда 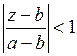 , отсюда
, отсюда 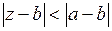 .
.
Искомое разложение имеет вид:
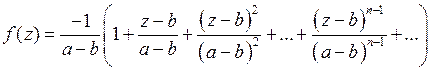 ,
,
или
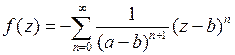 ;
; 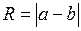 .
.
Пример 2. Разложить функцию 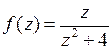 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 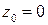 . Указать область, в которой справедливо это разложение.
. Указать область, в которой справедливо это разложение.
Решение.Для разложения в ряд Тейлора преобразуем данную функцию к виду 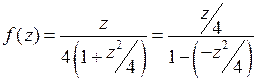 и воспользуемся формулой (2).
и воспользуемся формулой (2).
Так как 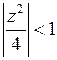 , то
, то 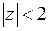 . Получаем искомое разложение:
. Получаем искомое разложение:
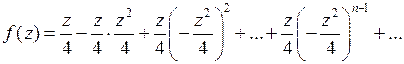 ,
,
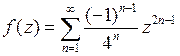 ;
; 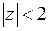
Ряд Лорана
Справедлива теорема:
Функция 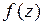 , аналитичная в кольце
, аналитичная в кольце 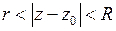 , представляется в этом кольце сходящимся рядом Лорана
, представляется в этом кольце сходящимся рядом Лорана
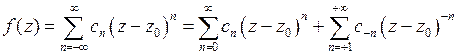 , (3)
, (3)
где
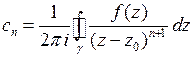 , (4)
, (4)
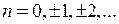 ,
, 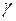 – любая окружность, ориентированная против часовой стрелки и лежащая внутри указанного кольца с центром в точке
– любая окружность, ориентированная против часовой стрелки и лежащая внутри указанного кольца с центром в точке 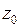 . Разложение в ряд Лорана единственно.
. Разложение в ряд Лорана единственно.
Первое слагаемое в разложении (3) называется правильной частью ряда Лорана, второе слагаемое – главной частью ряда Лорана. Правильная часть ряда Лорана сходится в круге 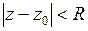 . Главная часть ряда Лорана сходится во внешности круга радиуса
. Главная часть ряда Лорана сходится во внешности круга радиуса 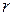 , то есть при
, то есть при 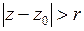 .
.
Разложение (3) иногда можно получить на практике, не применяя формулы (4) для коэффициентов 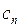 .
.
Пример 1. Найти все разложения функции 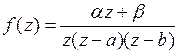 в ряд Лорана по степеням
в ряд Лорана по степеням 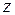 .
.
Решение.Пусть 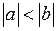 . Тогда данная функция может быть разложена в ряд Лорана в кольцах:
. Тогда данная функция может быть разложена в ряд Лорана в кольцах:
I) 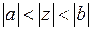 , II)
, II) 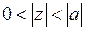 , III)
, III)  ,
,
где она является аналитической.
Разлагаем 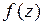 на элементарные дроби:
на элементарные дроби:
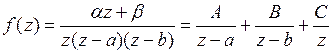 .
.
I. Дробь 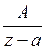 разлагается вне круга
разлагается вне круга 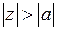 по степеням
по степеням 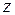 с отрицательными показателями, то есть
с отрицательными показателями, то есть
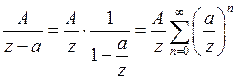 , при
, при 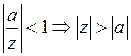 .
.
Дробь 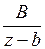 разлагается внутри круга
разлагается внутри круга 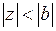 по степеням
по степеням 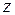 с положительными показателями, то есть
с положительными показателями, то есть
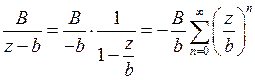 , при
, при 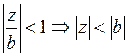 .
.
Итак, 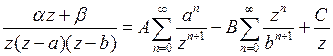 , при
, при 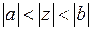 .
.
II. Дроби 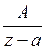 и
и 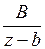 разложим в ряд по степеням
разложим в ряд по степеням 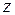 с положительными показателями внутри круга
с положительными показателями внутри круга 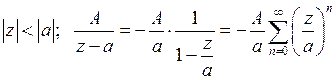 ,
,
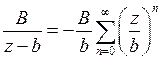 ,
, 
Итак, 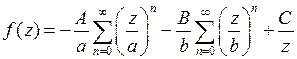 , при
, при 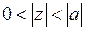 .
.
III. Дроби 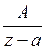 и
и 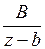 разложим по степеням
разложим по степеням 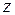 с отрицательными показателями, то есть
с отрицательными показателями, то есть
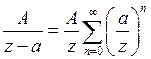 , где
, где 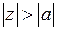 ;
; 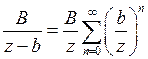 , где
, где 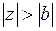 .
.
Итак, 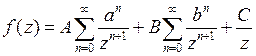 ,
, 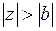 .
.
Пример 2.Найти все лорановские разложения 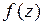 по степеням
по степеням 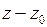 , если
, если 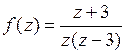 ,
, 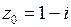 .
.
Решение.Пусть 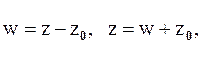
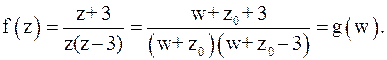
Точки  являются особыми точками функции
являются особыми точками функции 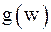 (в них
(в них 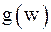 не аналитична). Тогда кольцами аналитичности
не аналитична). Тогда кольцами аналитичности 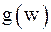 будут области:
будут области: 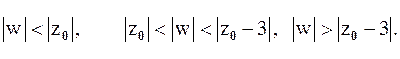
Возвращаясь к переменной 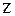 , получаем следующие области разложения
, получаем следующие области разложения 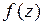 по степеням
по степеням 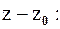
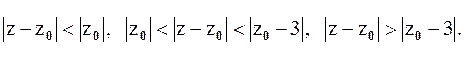
Рассмотрим разложение функции 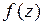 в ряд Лорана в кольце
в ряд Лорана в кольце 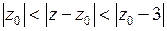 , то есть
, то есть 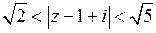 .
.
Представим функцию 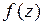 в виде
в виде
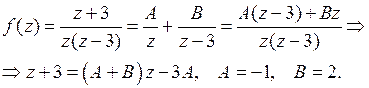

Таким образом, 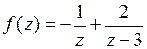 .
.
Дробь 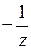 разложим по степеням
разложим по степеням 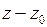 с отрицательными показателями вне круга
с отрицательными показателями вне круга 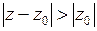 , то есть
, то есть
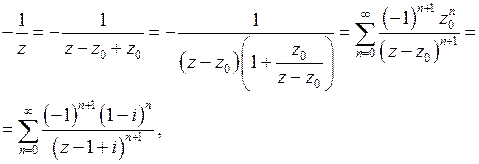
где 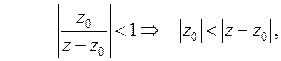
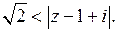
Дробь 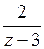 разложим по степеням
разложим по степеням 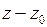 с положительными показателями внутри круга
с положительными показателями внутри круга 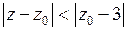 , то есть
, то есть
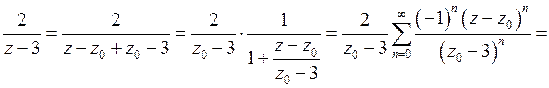
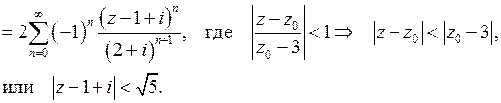
Итак,  ,
,
где 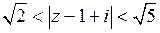 .
.
Остальные случаи разложения данной функции в ряд Лорана предлагается рассмотреть самостоятельно.
Для разложения функции в ряд Лорана иногда используют готовые разложения элементарных функций в ряд Тейлора.
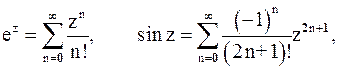
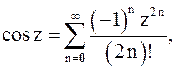
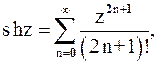
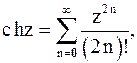 (5)
(5)
которые сходятся во всей комплексной плоскости.
Пример 3.Функцию 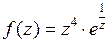 разложить в ряд Лорана в окрестности точки
разложить в ряд Лорана в окрестности точки 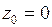 .
.
Решение.Функция 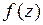 является аналитической в кольце
является аналитической в кольце 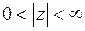 . Следовательно, она разложима в ряд Лорана. Воспользуемся разложением функции
. Следовательно, она разложима в ряд Лорана. Воспользуемся разложением функции 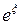 в ряд Тейлора
в ряд Тейлора 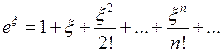 .
.
и положим 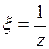 :
:
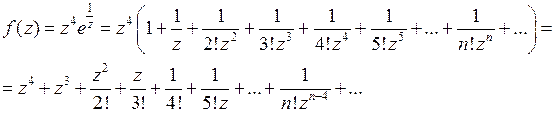 (6)
(6)
В силу единственности разложения в ряд Лорана (6) является рядом Лорана для функции 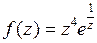 в кольце
в кольце 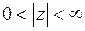 .
.
Дата добавления: 2022-05-27; просмотров: 242;











