Алгоритм на псевдокоде
Добавление в ДБ-дерево(D: Данные, p: pVertex)
Обозначим
VR, HR — логические переменные, определяющие вертикальный или горизонтальный рост дерева (в начале VR, HR равны ИСТИНА)
IF (p=NIL)
new(p); p→Date =D, p®Left= NIL; p→Right = NIL;
p→Balance=0; VR= ИСТИНА;
ELSE
IF (p→Date> D) Добавление в ДБ-дерево(D, p→Left)
IF (VR = ИСТИНА)
IF (p→Balance = 0) q:= p→Left; p→Left:= q→Right;
q→Right := p; p:=q; q→Balance :=1
VR := ЛОЖЬ; HR =ИСТИНА;
ELSE p→Balance:= 0; HR:=ИСТИНА;
FI
ELSE HR := ЛОЖЬ;
FI
ELSE IF (p→Date< D)
Добавление в ДБ-дерево (D, p→Right),
IF (VR = ИСТИНА) p→Balance:= 1; VR: = ЛОЖЬ;
HR := ИСТИНА;
ELSE IF (HR = ИСТИНА)
IF(p→Balancе > 0) q := p→Right;
p→Right := q→Left;
p→Balance := 0; q→Balance := 0;
p→Left := p; p :=q
VR:= ИСТИНА; HR:= ЛОЖЬ;
ELSE HR:= ЛОЖЬ;
FI
FI
FI
FI
FI
FI
 Примерпостроения двоичного Б-дерева приведен на следующем рисунке.
Примерпостроения двоичного Б-дерева приведен на следующем рисунке.
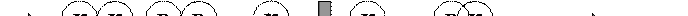
Рисунок 56 Построение двоичного Б-дерева
При построении двоичного Б-дерева реже приходится переставлять вершины, поэтому АВЛ-деревья предпочтительней в тех случаях, когда поиск ключей происходит значительно чаще, чем добавление новых элементов. Кроме того, существует зависимость от особенностей реализации, поэтому вопрос о применение того или иного тапа деревьев следует решать индивидуально для каждого конкретного случая.
13.6 Варианты заданий
1. Написать процедуру поиска элемента с заданным ключом в Б-дереве порядка m.
2. Определить трудоемкость поиска в Б-дереве порядка m.
3. Написать процедуру определения высоты Б-дерева порядка m.
4. Запрограммировать процедуру добавления нового элемента в Б-дерева порядка m.
5. Графически изобразить Б-дерево порядка 2.
6. Запрограммировать процедуру добавления новой вершины в двоичное Б-дерево. Определить количество необходимых операций для добавления вершины.
7. Написать процедуру определения высоты двоичного Б-дерева.
8. Экспериментально сравнить двоичное Б-дерево и ИСДП по высоте как двоичные деревья.
9. Экспериментально сравнить высоты двоичного Б-дерева и случайного дерева поиска как двоичные деревья.
10. Экспериментально сравнить двоичное Б-дерево и АВЛ-дерево по высоте как двоичные деревья.
11. Графически изобразить двоичное Б-дерево.
14. Деревья оптимального поиска (ДОП)
14.1 Определение дерева оптимального поиска
До сих пор предполагалось, что частота обращения ко всем вершинам дерева поиска одинакова. Однако встречаются ситуации, когда известна информация о вероятностях обращения к отдельным ключам. Обычно для таких ситуаций характерно постоянство ключей, т.е. в дерево не включаются новые вершины и не исключаются старые и структура дерева остается неизменной. Эту ситуацию иллюстрирует сканер транслятора, который определяет, является ли каждое слово программы (идентификатор) служебным. Статистические измерения на сотнях транслируемых программ могут в этом случае дать точную информацию об относительных частотах появления в тексте отдельных ключей.
Припишем каждой вершине дерева Vi вес wi, пропорциональный частоте поиска этой вершины (например, если из каждых 100 операций поиска 15 операций приходятся на вершину V1, то w1=15). Сумма весов всех вершин дает вес дерева W. Каждая вершина Vi расположена на высоте hi, корень расположен на высоте 1. Высота вершины равна количеству операций сравнения, необходимых для поиска этой вершины. Определим средневзвешенную высоту дерева с n вершинами следующим образом: hср=(w1h1+w2h2+…+wnhn)/W. Дерево поиска, имеющее минимальную средневзвешенную высоту, называется деревом оптимального поиска (ДОП).
Пример. Рассмотрим множество из трех ключей V1=1, V2=2, V3=3 со следующими весами: w1=60, w2=30, w3=10, W=100. Эти три ключа можно расставить в дереве поиска пятью различными способами.
 |  |
Рисунок 57 Различные деревья поиска с вершинами V1=1, V2=2, V3=3
Легко видеть, что минимальной средневзвешенной высотой обладает дерево 1 на рисунке 57, которое представляет собой список или вырожденное дерево. Дерево 3 не является деревом оптимального поиска, хотя представляет собой идеально сбалансированное дерево. Очевидно, для минимизации средней длины пути поиска нужно стремится располагать наиболее часто используемые вершины ближе к корню дерева.
Задача построения ДОП может ставится в двух вариантах:
· Известны вершины и их веса.
· Вес вершины определяется в процессе работы. Например, после каждого поиска вершины ее вес увеличивается на 1. В этом случае необходимо перестраивать структуру дерева при изменении весов.
Далее будем рассматривать задачупостроения ДОП с фиксированным набором ключей и их весов.
14.2 Точный алгоритм построения ДОП
Поскольку число возможных конфигураций из n вершин растет экспоненциально с ростом n, то решение задачи построения ДОП при больших n методом перебора нерационально. Однако деревья оптимального поиска обладают свойствами, которые позволяют получить алгоритм построения ДОП, начиная с отдельных вершин с последовательным включением новых вершин в дерево. Далее будем считать, что множество вершин, входящих в дерево, упорядочено. Поскольку вес дерева остается неизменным, то вместо средневзвешенной высоты будем рассматривать взвешенную высоту дерева: P=h1w1+h2w2+…+hnwn
Свойство 1. Для дерева поиска с весом W справедливо соотношение P=PL+W+PR, где PL, PR – взвешенные высоты левого и правого поддеревьев корня.
Доказательство. Пусть вершина Vi с весом wi является корневой для некоторого i=1, …n. Поскольку левое и правое поддеревья являются деревьями поиска, то в левое поддерево входят вершины V1, V2, …, Vi-1, а в правое – Vi+1, …, Vn. Взвешенные высоты этих поддеревьев вычисляются следующим образом.
PL = (h1-1)w1+(h2-1)w2+…+(hi-1-1)wi-1
PR = (hi+1-1)wi+1+ …+ (hn-1)wn
Рассмотрим выражение взвешенной высоты для всего дерева, замечая, что hi=1
P=h1w1+h2w2+…+hnwn= (h1-1)w1 + w1+(h2-1)w2+ w2…+(hi-1-1)wi-1 + wi-1 +
+ wi + (hi+1-1)wi+1+ wi+1 …+ (hn-1)wn + wn = PL+W+PR
Свойство 2. Все поддеревья дерева оптимального поиска также являются деревьями оптимального поиска для соответствующих подмножеств вершин.
Доказательство. Предположим, что одно из поддеревьев, например, правое, не является ДОП, т.е. существует дерево поиска с тем же множеством вершин, но с меньшей взвешенной высотой. Тогда по свойству 1 взвешенная высота всего дерева также не является минимальной. Данное противоречие доказывает свойство 2.
На основе приведенных свойств можно разработать точный алгоритм построения ДОП. Обозначим Tij – оптимальное поддерево, состоящее из вершин Vi+1, …, Vj. Введем матрицу АR=||Arij||, 0≤i,j≤n элементы которой содержат номер корневой вершины поддерева Tij, 0≤i<j≤n. Взвешенную высоту поддерева Tij обозначим Apij, а вес поддерева Tij обозначим Awij, 0≤i<j≤n. Очевидно, что P=Apo,n, W=Awo,n, Тii – пустые деревья (без вершин), Awii=0, Apii=0, i=1, …n.
Используя свойство 2, величины Awij, Apij можно вычислить рекуррентно по следующим соотношениям (для всех возможных поддеревьев):
Awij=Awi,j-1+Awj, 0≤ i < j ≤ n (1)
Apij=Awij+min (Api,k-1+Apk,j), 0≤ i < j ≤ n (2)
i<k≤j
Во время вычислений будем запоминать индекс k*, при котором достигается минимум во втором соотношении. Значение k* является индексом корневой вершины поддерева Tij во всем множестве вершин. Занесем в матрицу АR k* –индекс корня Tij, т.е. Arij = k*, 0≤i<j≤n.
Идея построения дерева состоит в следующем. В матрице АR берем значение Aro,n (номер корневой вершины всего дерева в упорядоченном массиве вершин), пусть оно равно k. Добавляем вершину Vk в дерево, используя обычный алгоритм добавления вершин в дерево поиска. Затем из матрицы АR берем значения Aro,k-1 и добавляем вершину с этим номером в левое поддерево. Далее берем Ark,n и добавляем вершину с этим номером в правое поддерево и т.д.
Пример. Построить дерево оптимального поиска с вершинами V1=1, V2=2, V3=3 и весами w1=60, w2=30, w3=10. Сначала вычислим Awij, Apij, Arij, 0≤i<j≤n. Легко видеть, что
T00, T11, T22, T33 – пустые поддеревья
T01, T12, T23 – поддеревья из одной вершины (1), (2), (3)
T02, T13 – поддеревья из двух вершин (1,2) и (2,3)
T03 – поддерево из трех вершин (1,2,3)
По формулам (1) и (2) вычислим элементы матрицы весов AW и элементы матрицы взвешенных высот AP, значения матрицы АR запишем в верхних уголках ячеек матрицы АP.
| Аwij | ||||
| Аpij | ||||
| 601 | 1201 | 1501 | ||
| 302 | 502 | |||
| 103 | ||||
Аp01=Аw01+min(Аp00+Аp11) =60 (k*=1)
0<k≤1
Аp12=Аw12+min(Аp11+Аp22) =30 (k*=2)
1<k≤2
Аp23=Аw23+min(Аp22+Аp33) =10 (k*=3)
2<k≤3
Аp02=Аw02+min(Аp00+Аp12, Аp01+Аp22)=90+30=120 (k*=1).
0<k≤2 k=1 k=2
Аp13=Аw13+min(Аp11+Аp23, Аp12+Аp33)=40+10=50 (k*=2).
1<k≤3 k=2 k=3
Аp03=Аw03+min(Аp00+Аp13, Аp01+Аp23, Аp02+Аp33)=100+50=150 (k*=3).
0<k≤3 k=1 k=2 k=3
Корневой вершиной будет вершина V1, поскольку Аr0,3=1. Левое поддерево пустое, корень правого поддерева – вершина V2 (r1,3=2) и т.д. Полученное дерево показано на рисунке.

Рисунок 58 ДОП для w1=60, w2=30, w3=10
Поскольку существует около n2/2 значений Аpij , а вычисление (2) требует выбора одного из 0<i-j£ n значений, то весь процесс будет занимать О(n3) операций при n→∞. Д. Кнут отмечает, что можно избавиться от одного множителя n и тем самым сохранить практическую ценность алгоритма. Поиск Аrij можно ограничить, то есть сократить число вычислений до j-i (если найден корень оптимального поддерева Tij, то ни добавление справа новой вершины, ни отбрасывание левой вершины не могут сдвинуть вправо этот оптимальный корень). Это свойство выражается соотношением Аri,j-1 ≤ Аrij ≤ Аri+1,j , что и ограничивает поиск Аrij диапазоном Аri,j-1…Аri+1,j. Это уменьшает трудоемкость алгоритма до О(n2) операций при n→∞.
Дата добавления: 2022-02-05; просмотров: 382;











