Алгоритм на псевдокоде

del (r: pVertex, Уменьшение: boolean)

IF (r→right ≠ NIL)

del (r→right, Уменьшение)

IF Уменьшение BR (r, Уменьшение) FI

ELSE q→Data := r→Data

q := r

r := r→Left

Уменьшение := ИСТИНА

FI

Пример: Удаление из АВЛ-дерева вершин B 9 2 4 1 7 E F

Рисунок 48 Удаление из АВЛ-дерева

Поиск элемента с заданным ключом, включения нового элемента, удаления элемента – каждое из этих действий в АВЛ-дереве можно произвести в худшем случае за О(log n) операций.

Отличие между процедурами включения и удаления заключается в следующем. Включение может привести самое большое к одному повороту, исключение может потребовать поворот во всех вершинах вдоль пути поиска. Наихудшим случаем с точки зрения количества балансировок является удаление самой правой вершины у плохого АВЛ-дерева (дерева Фибоначчи). По экспериментальным оценкам на каждые два включения встречается один поворот, а при исключении поворот происходит в одном случае из пяти.

12.5 Варианты заданий

1. Написать процедуру, которая определяет, является ли двоичное дерево АВЛ-деревом. Проверить правильность работы процедуры на различных двоичных деревьях.

2. Написать процедуру для построения деревьев Фибоначчи заданной высоты.

3. Экспериментально определить среднюю длину пути в дереве Фибоначчи.

4. Запрограммировать процедуру добавления новой вершины в АВЛ-дерево. Определить количество необходимых операций для добавления вершины.

5. Запрограммировать процедуру удаления вершины из АВЛ-дерева. Определить количество необходимых операций для удаления вершины.

6. Экспериментально сравнить АВЛ-дерево и ИСДП по высоте.

7. Экспериментально сравнить высоты АВЛ-дерева и случайного дерева поиска.

8. Экспериментально определить количество поворотов на одно включение вершины в дерево.

9. Экспериментально определить количество поворотов на одно исключение вершины из дерева.

10. Графически изобразить АВЛ-дерево.

13. Б-ДЕРЕВЬЯ

13.1 Определение Б-дерева порядка m

Деревья, имеющие вершины со многими потомками, будем называть сильноветвящимися. Такие деревья могут быть эффективно использованы для решения следующей задачи: формирование и поддержание крупномасштабных деревьев поиска, для которых необходимы включения и удаление элементов, но для которых либо не хватает оперативной памяти, либо она слишком дорога для долговременного использования.

В этом случае вершины дерева могут храниться во внешней памяти (например, на диске), тогда ссылки представляют собой адреса на диске, а не в оперативной памяти. Если использовать двоичное дерево для n = 10⁶ элементов, то потребуется log(10⁶) = 20 шагов поиска. Так как каждый шаг включает в себя обращение к диску, то необходимо минимизировать число обращений к диску. Сильноветвящиеся деревья – идеальное решение этой проблемы, т.к. при обращении к диску можно считывать не один элемент, а целую группу, причём размер сектора диска определяет размер минимальной порции (обычно кратен 512 байт). Таким образом, за одно обращение считывается поддерево, которое будем называть страницей. Например, пусть для дерева из 10⁶ элементов размер страницы равен 100 вершин. Поиск будет требовать в среднем log₁₀₀(10⁶) = 3, а не 20 обращений к диску. Однако если дерево растёт случайным образом, то в худшем случае может потребоваться даже 10⁴ обращений. Поэтому Р. Байером и Е. Маккрейтом был сформулирован критерий управления ростом дерева: каждая страница (кроме одной) должна содержать (при заданном постоянном m) от m до 2m элементов.

Таким образом, для дерева с n элементами и максимальном размером в 2m вершин в худшем случае потребуется log_mn обращений к страницам (диску). При этом коэффициент использования памяти не меньше, чем 50%, так как страницы всегда заполнены минимум наполовину. Также эта схема позволяет достаточно просто осуществлять поиск, включения и удаления элементов.

Введем следующее определение. Б – дерево порядка m – это дерево со следующими свойствами:

1. В каждой странице хранится k элементов данных d₁ < d₂ < ... < d_k и k+1 указатель p₀, p₁, ...p_k. Каждый указатель p_i либо равен NIL, либо указывает на вершину, все элементы которой больше d_i, но меньше d_i+1.

Рисунок 49 Страница Б-дерева

2. Для каждой вершины, кроме корня m ≤ k ≤ 2m, для корня 1 ≤ k ≤ 2m.

3. Все листья дерева расположены на одном уровне.

Пример Б-дерева при m = 2.

Рисунок 50 Пример Б-дерева

Очевидно, количество обращений к диску равно высоте Б-дерева. Легко видеть, что минимальное количество вершин в Б-дереве при заданной высоте h определяется равенством n_min = 2(m+1)^h-1 – 1. Отсюда высота Б-дерева порядка m с n элементами данных 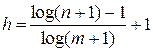. Например, при m =255 высота h меньше, чем log n/8, т.е. по сравнению с обычными двоичными деревьями требуется в 8 раз меньше обращений к диску.

13.2 Поиск в Б-дереве

Если спроецировать Б – дерево на один уровень, то элементы расположатся в возрастающем порядке слева направо. Такое размещение определяет способ поиска элемента с заданным ключом. Страница считывается в оперативную память, а затем производится поиск среди элементов d₁, d₂, …,d_k (упорядоченных!). Если k мало, то можно использовать простой последовательный поиск, если k достаточно большое, то – двоичный поиск.

Будем считать, что элементы на странице представлены в виде массива. Тогда структура данных может быть следующим образом описана (на Паскале):

type pPage = ^Page; {указатель на страницу}

Item = record {тип элемента}

Data: integer;

p: pPage;

end;

Page = record {тип страницы}

k: 0 . . 2*m;

p0: pPage;

e: array [1 . . 2*m] of Item;

end;

где m – порядок Б – дерева,

k – количество элементов на странице,

p0 – указатель на страницу с элементами < d₁,

e – массив элементов на странице.

Рисунок 51 Структура страницы Б-дерева