Алгоритм на псевдокоде

Разделение корневой страницы

Root := NIL

DO <ввести D>

Построение Б-дерева (D, Root, Rost, u)

IF (Rost = true) (включение новой корневой страницы)

q :=Root

new(Root)

root→k := 1

root→p₀ := q

root→e₁:= u

FI

OD

13.4 Определение двоичного Б-дерева

На первый взгляд кажется, что наименьший интерес представляют Б-деревья первого порядка. Но иногда стоит обращать внимание и на такие исключительные варианты. Очевидно, что Б-дерево первого порядка не имеет смысла использовать для представления больших множеств данных, требующих вторичной памяти, т.к. приблизительно 50% всех страниц будут содержать только один элемент.

Двоичное Б-дерево состоит из вершин (страниц) с одним или двумя элементами. Следовательно, каждая страница содержит две или три ссылки на поддеревья. На рисунке 53 показаны примеры страниц Б – дерева при m = 1.

Рисунок 53 Виды вершин ДБД

Поэтому вновь рассмотрим задачу построения деревьев поиска в оперативной памяти компьютера. В этом случае неэффективным с точки зрения экономии памяти будет представление элементов внутри страницы в виде массива. Выход из положения – динамическое размещение на основе списочной структуры, когда внутри страницы существует список из одного или двух элементов.

Рисунок 54 Вершины двоичного Б-дерева

Таким образом, страницы Б-дерева теряют свою целостность и элементы списков начинают играть роль вершин в двоичном дереве. Однако остается необходимость делать различия между ссылками на потомков (вертикальными) и ссылками на одном уровне (горизонтальными), а также следить, чтобы все листья были на одном уровне.

Очевидно, двоичные Б-деревья представляют собой альтернативу АВЛ-деревьям. При этом поиск в двоичном Б-дереве происходит как в обычном двоичном дереве.

Высота двоичного Б-дерева 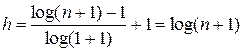. Если рассматривать двоичное Б-дерево как обычное двоичное дерево, то его высота может увеличиться вдвое, т.е. 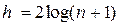. Для сравнения, в АВЛ-дереве даже в самом плохом случае h<1.44 log n. Поэтому сложность поиска в двоичном Б-дереве и в АВЛ-дереве одинакова по порядку величины.

13.5 Добавление вершины в дерево

Построение двоичного Б-дерева происходит путем добавления новой вершины в уже существующее дерево. Введем логическую переменную VR, показывающую вертикальный рост дерева (в случае, если страница переполнилась и средний элемент передается на вышележащий уровень) и логическую переменную HR, определяющую горизонтальный рост дерева (если новый элемент размещается на этой же условной странице). Также определим показатель баланса BAL для каждой вершины, который принимает значение 0, если у данной вершины есть только вертикальные ссылки (вершина одна на странице), и значение 1, если у данной вершины есть правая горизонтальная ссылка.

При добавлении элементов в двоичное Б-дерево различают 4 ситуации, возникающих при росте левых или правых поддеревьев (см. рис. 55). Самый простой случай (1) — рост правого поддерева вершины А, когда А — единственный элемент на странице. Тогда вертикальная ссылка просто превращается в горизонтальную (HR=1, баланс вершины А равен 1). Если на странице уже два элемента (2), то при добавлении новой вершины С средняя вершина В передается на вышестоящий уровень (VR=1, баланс вершины В равен 0).

В случае роста левого поддерева, если вершина В одна на странице (3), то вершина А добавляется на эту страницу. Однако левая ссылка не может быть горизонтальной, поэтому требуется переопределение ссылок (HR=1, баланс вершины А равен 1). Если на странице два элемента, то, как и в случае 2, средняя вершина В поднимается на вышестоящий уровень (VR=1, баланс вершины В равен 0).

Рисунок 55 Четыре ситуации, возникающих при росте левых или правых поддеревьев