Алгоритм на псевдокоде
Сортировка части массива с границами (L,R).
Обозначим: L-левую границу рабочей части массива
R-правую границу рабочей части массива
х:=аL, i:=L, j:=R,
DО (i£j)
DО (ai<x) i:=i+1 OD
DО (aj>x) j:=j-1 OD
IF (i<=j)
ai↔ aj,, i:=i+1, j:=j-1
FI
OD
IF (L<j)
<Сортировка части массива с границами (L,j)>
FI
IF (i<R)
<Сортировка части массива с границами (i,R)>
FI
Очевидно, трудоёмкость метода существенно зависит от выбора элемента х, который влияет на разделение массива. Максимальные значения М и С для метода быстрой сортировки достигаются при сортировке упорядоченных массивов (в прямом и обратном порядке). Тогда в этом случае в одной части остаётся только один элемент (минимальный или максимальный), а во второй – все остальные элементы. Выражения для М и С имеют следующий вид
M=3(n-1), C=(n2+5n+4)/2
Таким образом, в случае упорядоченных массивов трудоёмкость сортировки имеет квадратичный порядок.
Элемент am называется медианой для элементов aL…aR, если количество элементов меньших am равно количеству элементов больших am с точностью до одного элемента (если количество элементов нечётно). В примере буква К- медиана для КУРАПОВАЕ.
Минимальная трудоемкость метода Хоара достигается в случае, когда на каждом шаге алгоритма в качестве ведущего элемента выбирается медиана массива. Количество сравнений в этом случае C=(n+1)log(n+1)-(n+1). Количество пересылок зависит от положения элементов, но не может быть больше одного обмена на два сравнения. Поэтому количество пересылок – величина того же порядка, что и число сравнений. Асимптотические оценки для средних значений М и С имеют следующий вид
С=О(n log n), М=О(n log n) при n → ∞.
Метод Хоара неустойчив.
4.3 Проблема глубины рекурсии.
В теле подпрограммы доступны все объекты, описанные в основной программе, в том числе и имя самой подпрограммы. Это позволяет внутри тела подпрограммы осуществлять её вызов. Процедуры и функции, организующие вызовы «самих себя» называются рекурсивными. Рекурсия широко используется в программирование, потому что многие математические алгоритмы имеют рекурсивную природу.
В качестве примера приведём известный алгоритм вычисления факториала неотрицательного целого числа:
0!=1
1!=1
n!=(n-1)!*n
function fact (n:word):longint;
begin
if (n=0) or (n=1) then fact:=1
else fact:=fact(n-1)*n;
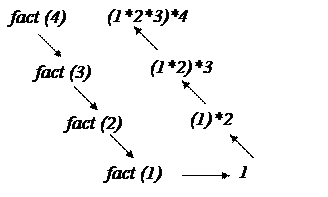 end;
end;
Рисунок 10 Схема вызовов при вычислении 4!
Рекурсивное оформление программы более компактно, наглядно и эффективно. Но существует опасность переполнения стека. Каждый вызов подпрограммы требует специально отведённой области памяти, называемой фреймом. В ней хранятся фактические параметры, адреса возврата, локальные переменные и регистры УП.
Фрейм
| Практический параметр |
| Адрес возврата |
| Регистры из программы |
| Локальные переменные |
Рисунок 11 Структура фрейма
При выходе из программы эта память освобождается. Но если подпрограмма вызывает другую подпрограмму или саму себя, то в дополнение к существующему фрейму создаётся новый, т.е. n вложенных вызовов требуют выделения n фреймов в памяти.
Рассмотренный алгоритм Хоара может потребовать n вложенных вызовов (n – размер массива), т.е. глубина рекурсии достигает n. Это большой недостаток предложенного алгоритма. Попробуем уменьшить глубину рекурсии до log n. В рассмотренном алгоритме производится 2 рекурсивных вызова. Но один из них можно заменить простой итерацией, т.е. для одной части массива будем применять рекурсию, а для другого – простую итерацию. Чтобы уменьшить глубину рекурсии нужно делать рекурсивный вызов для меньшей по размеру части массива. Тогда в худшем случае, когда размеры правой и левой частей будут одинаковые, максимальная глубина рекурсии будет не больше log n. Например, для массива из 1 млн. элементов понадобиться одновременно менее 20 фреймов в памяти. Запишем новую версию алгоритма:
Дата добавления: 2022-02-05; просмотров: 453;











