Глава 7. Алгоритмы.

Понятие алгоритма в настоящее время широко используется, тем не менее, строго это понятие не определено.

В математике алгоритм означает точное предписание, которое задает вычислительный процесс, начинающийся с исходных данных и направленный на получение полностью определенного исходными данными результата (см., например, [9]).

Примерами алгоритмов являются:

§ Правила выполнения сложения и умножения натуральных чисел. Исходными данными являются пары натуральных чисел, результатом – натуральное число.

§ Правило отыскания корней квадратного уравнения с действительными коэффициентами. Исходными данными являются коэффициенты уравнения 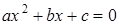, результатом – два (может быть, равных) корня квадратного уравнения (если результат ищется в комплексных числах). Если результат обязательно должен быть действительным числом, то при результат получен не будет.

§ Правило отыскания производной многочлена степени n. Исходными данными являются коэффициенты многочлена, результатом – коэффициенты производной многочлена.

Алгоритм может оперировать не только с числами, но и с любыми символами и их последовательностями (словами). Следовательно, алгоритм можно понимать более широко, как тот или иной способ или путь решения некоторой задачи. Примерами могут быть: алгоритм расстановки мебели в квартире, алгоритм строительства дома и т.д.

Алгоритм должен удовлетворять следующим требованиям.

· Массовость алгоритма. Алгоритм применяется к исходным данным, которые выбираются из потенциально бесконечного множества.

· Дискретность алгоритма. Для размещения данных необходима однородная и дискретная, то есть организованная в виде одинакового количества ячеек, память.

· Элементарность шагов алгоритма. Закон получения последующей системы величин из предшествующей системы должен быть простым.

· Детерминированность алгоритма. Величины, получаемые на каком-либо (не начальном) этапе решения задачи, должны однозначно определяться величинами, полученными на предшествующих этапах. Кроме того, после каждого шага алгоритма должно быть указано, какой шаг выполняется дальше, либо дается команда остановки.

· Результативность алгоритма. После конечного числа шагов работа должна быть остановлена с указанием того, что считать результатом.

Можно выделить семь параметров, характеризующих алгоритм:

1) совокупность возможных исходных данных;

2) совокупность возможных результатов;

3) совокупность возможных промежуточных результатов;

4) правило начала;

5) правило непосредственной переработки;

6) правило окончания;

7) правило извлечения результата.

Мы рассмотрим элементы теории алгоритмов – рекурсивные функции и машины Тьюринга.

В Содержание.