Принцип двойственности.

Пусть Т – произвольная программа (машина Тьюринга). Обозначим Т* программу, которая получается из Т заменой (во всех командах) R на L и наоборот. Программа Т* называется двойственной к Т.

Пример.Машина Тьюринга в произвольной записи, начиная с любой ячейки, двигаясь вправо, находит первый нуль. Соответствующая программа имеет вид:

.

Возможны три случая.

1. В начальный момент головка машины обозревает нуль. Машина останавливается.

2. В начальный момент головка машины обозревает единицу, и справа от начальной ячейки есть хотя бы один нуль. Машина переместит головку через массив единиц вправо и остановится перед первым нулем.

3. В начальный момент головка машины обозревает единицу, и справа от начальной ячейки запись состоит только из единиц. Машина будет перемещать головку через массив единиц вправо, не останавливаясь.

В программе заменим символ R на L. Получим программу:

.

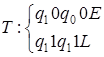Данная программа будет двойственной к предыдушей. Непосредственной проверкой можно убедиться, что головка машины, двигаясь влево, будет отыскивать первый нуль.

Очевидно, что (Т*)*=Т, то есть понятие двойственности является взаимным. Машины Тьюринга, соответствующие двойственным программам, будем называть двойственными машинами Тьюринга.

Из примера было видно, что двойственные машины функционируют симметричным образом. Так, пусть в начальный момент времени имеется конфигурация

,

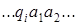и машина Т в момент времени t переработает ее в конфигурацию

.

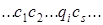В то же время, двойственная машина Т* конфигурацию

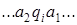
(симметричную первой конфигурации относительно 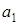) в момент времени t переработает в конфигурацию

,

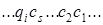симметричную второй конфигурации относительно .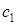

В Содержание.