Способы композиции машин Тьюринга.
1. Последовательное подключение одной машины Тьюринга к другой. Пусть 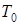 и
и 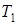 – две машины Тьюринга над алфавитом {0,1}, множества состояний машин не пересекаются. Перенумеруем 0,1,…,l-1 все команды с
– две машины Тьюринга над алфавитом {0,1}, множества состояний машин не пересекаются. Перенумеруем 0,1,…,l-1 все команды с  программы
программы 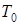 . Пусть p(x) – предикат на множестве {0,1,…,l-1}. Последовательное подключение
. Пусть p(x) – предикат на множестве {0,1,…,l-1}. Последовательное подключение 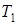 к
к 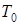 (относительно предиката p(x)) – это машина Тьюринга
(относительно предиката p(x)) – это машина Тьюринга 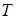 , которая получается следующим образом. Первая половина таблицы для
, которая получается следующим образом. Первая половина таблицы для 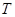 совпадает с таблицей
совпадает с таблицей 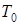 для тех клеток, в которых нет команды с
для тех клеток, в которых нет команды с  .
.
Если p(n)=1, то в клетке n – команда 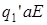 ,
, 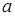 – номер строки (0 или 1), где находится клетка n,
– номер строки (0 или 1), где находится клетка n, 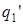 – начальное состояние
– начальное состояние 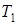 .
.
Если p(n)=0, то в клетке n – команда с  . Вторая половина таблицы Т полностью совпадает с таблицей
. Вторая половина таблицы Т полностью совпадает с таблицей 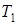 .
.
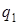 … … 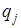 … … 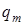
| 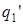 … … 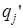 … … 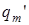
| |
В частном случае, если  – начальное состояние машины
– начальное состояние машины 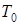 , а
, а 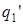 – начальное состояние
– начальное состояние 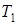 , заменим в программе
, заменим в программе 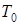 состояние
состояние  на состояние
на состояние 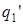 , и полученную программу объединим с программой
, и полученную программу объединим с программой 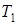 . В результате мы получим программу для машины
. В результате мы получим программу для машины 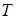 , которая является композицией машин
, которая является композицией машин 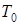 и
и 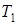 по паре состояний (
по паре состояний (  ,
, 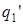 ).
).
2. Итерация машины Тьюринга. Пусть 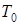 – машина Тьюринга над алфавитом {0,1}. Перенумеруем 0,1,…,l-1 все команды с
– машина Тьюринга над алфавитом {0,1}. Перенумеруем 0,1,…,l-1 все команды с  программы
программы 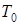 . Пусть p(x) – предикат на множестве {0,1,…,l-1}. Итерация машины Тьюринга
. Пусть p(x) – предикат на множестве {0,1,…,l-1}. Итерация машины Тьюринга 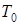 относительно предиката p(x) – это машина Тьюринга Т, которая получается следующим образом. Таблица Т совпадает с таблицей
относительно предиката p(x) – это машина Тьюринга Т, которая получается следующим образом. Таблица Т совпадает с таблицей 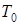 для тех клеток, в которых нет команды не с
для тех клеток, в которых нет команды не с  .
.
Если p(n)=1, то в клетке n – команда 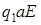 , a – номер строки, где находится клетка n,
, a – номер строки, где находится клетка n, 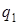 – начальное состояние
– начальное состояние 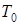 .
.
Если p(n)=0, то в клетке n – команда с  .
.
Действительно, имеет место итерация, т.е. многократная работа машины 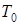 .
.
В частном случае, если  – заключительное состояние машины
– заключительное состояние машины 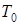 , а
, а 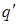 – любое состояние машины
– любое состояние машины 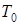 , не являющееся заключительным, то заменим в программе
, не являющееся заключительным, то заменим в программе 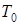 состояние
состояние  на состояние
на состояние 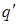 . В результате мы получим программу для машины Т, которая является итерацией машины
. В результате мы получим программу для машины Т, которая является итерацией машины 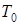 по паре состояний (
по паре состояний (  ,
, 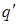 ).
).
Отметим, что начальных и заключительных состояний может быть несколько.
В Содержание.
Задачи.
1. По заданной машине Тьюринга 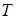 и начальной конфигурации
и начальной конфигурации 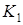 найти заключительную конфигурацию:
найти заключительную конфигурацию:
1) 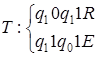 ;
; 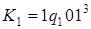 .
.
2) 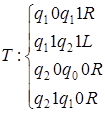 ;
; 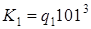 .
.
3)  ;
; 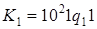 .
.
4) 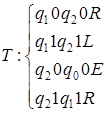 ;
; 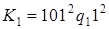 .
.
5) 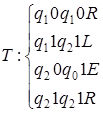 ;
; 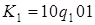 .
.
6) 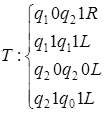 ;
; 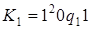 .
.
7) 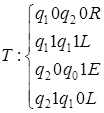 ;
; 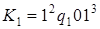 .
.
8) 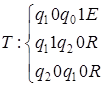 ;
; 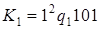 .
.
9) 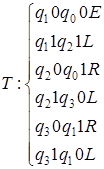 ;
; 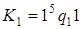 .
.
10) 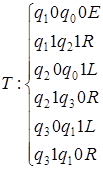 ;
; 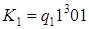 .
.
2. Выяснить, применима ли машина Тьюринга 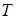 к слову
к слову 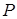 . Если применима, то записать результат
. Если применима, то записать результат 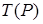 применения машины
применения машины 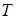 к слову
к слову 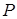 . Предполагается, что в начальный момент времени головка машины обозревает самую левую единицу слова.
. Предполагается, что в начальный момент времени головка машины обозревает самую левую единицу слова.
1) 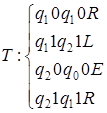 ; а)
; а) 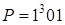 ; б)
; б) 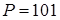 .
.
2) 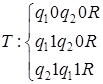 ; а)
; а) 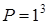 ; б)
; б) 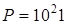 .
.
3) 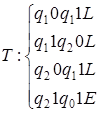 ; а)
; а) 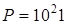 ; б)
; б) 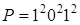 .
.
4) 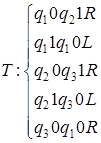 ; а)
; а) 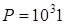 ; б)
; б) 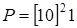 .
.
5) 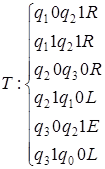 ; а)
; а) 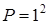 ; б)
; б) 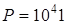 .
.
3. Построить в алфавите {0,1} машину Тьюринга, обладающую свойствами:
1) машина имеет одно состояние, одну команду и применима к любому слову в алфавите {0,1};
2) машина имеет одно состояние, две команды, не применима ни к какому слову в алфавите {0,1}, и в процессе работы головка обозревает бесконечное множество ячеек;
3) машина имеет две команды, не применима ни к какому слову в алфавите {0,1}, и в процессе работы головка обозревает одну ячейку.
Предполагается, что в начальный момент времени головка машины обозревает самый левый символ слова.
4. По словесному описанию машины Тьюринга построить ее программу (в алфавите {0,1}).
1) Начав работу с первой единицы массива из единиц, машина “сдвигает” его на две ячейки вправо, не изменяя остального содержимого ленты, и останавливается на последней единице перенесенного массива.
2) Начав двигаться влево от произвольной ячейки, головка находит первую при таком перемещении ячейку с единицей (если такая встретится на пути) и, сделав один шаг вправо, останавливается на соседней ячейке. Содержимое ленты не меняется.
3) Машина начинает работу с самой левой непустой ячейки и отыскивает нуль, примыкающий с левой стороны к первому справа массиву из трех единиц, окаймленному нулями. Головка останавливается на первой единице найденного массива (если такой есть). Содержимое ленты не меняется.
4) Головка машины, начав работу с произвольной ячейки, содержащей единицу, двигается влево до тех пор, пока не пройдет подряд пять нулей. Головка останавливается на первой ячейке слева за этими пятью нулями, напечатав в ней единицу. Остальное содержимое ленты не меняется.
5) При заданном 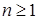 головка машины, начав работу с произвольной ячейки и двигаясь вправо, записывает подряд
головка машины, начав работу с произвольной ячейки и двигаясь вправо, записывает подряд 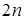 нулей и останавливается на последнем из них.
нулей и останавливается на последнем из них.
6) Головка машины, двигаясь вправо от какой-либо пустой ячейки, находит первый при таком перемещении массив, содержащий не менее семи единиц, стирает в нем первые семь единиц и останавливается на самой правой из ячеек, в которых были стерты единицы. Остальное содержимое ленты не меняется.
7) При заданном значении n головка машины из n записанных единиц оставляет на ленте 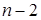 единицы, так же записанных подряд, если
единицы, так же записанных подряд, если 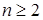 , и работает вечно, если
, и работает вечно, если 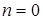 или
или 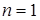 .
.
8) Машина реализует алгоритм вычисления функции 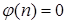 , считая, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.
, считая, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.
9) Машина реализует алгоритм вычисления функции 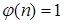 , считая, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.
, считая, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.
10) Машина реализует алгоритм вычисления функции 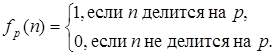
Считается, что число n представляется записанными подряд n единицами, и массив из n единиц уже найден.
11) Показать, что для всякой машины Тьюринга существует эквивалентная ей машина, в программе которой отсутствуют заключительные состояния.
12) Показать, что для всякой машины Тьюринга существует эквивалентная ей машина, в программе которой отсутствует символ E.
5. Для машин Тьюринга из задачи 1 построить двойственные машины.
6. Построить композицию 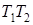 машин Тьюринга
машин Тьюринга 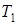 и
и 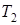 по паре состояний (
по паре состояний ( 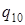 ,
, 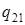 ) и найти результат применения композиции
) и найти результат применения композиции 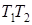 к слову
к слову 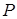 .
.
| 1) | 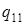
| 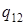
| 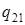
| 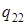
| |||
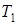 : :
| 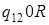
| 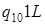
| , 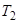 : :
| 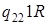
| 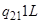
| ||
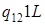
| 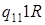
| 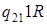
| 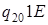
|
а) 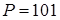 ; б)
; б) 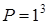 .
.
| 2) | 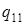
| 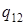
| 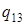
| |
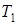 : :
| 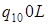
| 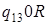
| 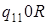
| |
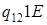
| 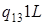
| 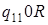
|
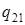
| 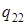
| ||
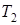 : :
| 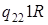
| 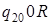
| |
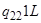
| 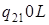
|
а) 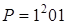 ; б)
; б) 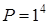 .
.
| 3) | 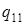
| 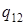
| 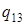
| |
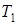 : :
| 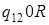
| 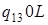
| 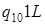
| |
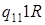
| 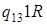
| - |
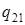
| 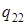
| 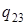
| ||
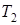 : :
| 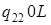
| 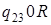
| 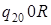
| |
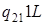
| 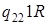
| 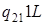
|
а) 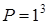 ; б)
; б) 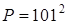 .
.
7. Найти результат применения итерации машины 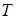 по паре состояний (
по паре состояний (  ,
, 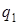 ) к слову
) к слову 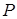 (заключительными состояниями являются
(заключительными состояниями являются  и
и 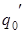 ).
).
1)
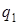
| 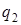
| 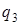
| 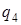
| 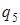
| ||
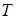 : :
| 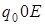
| 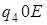
| 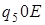
| 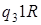
| 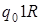
| |
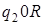
| 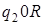
| 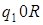
| - | - |
а) 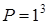 ; б)
; б) 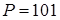 .
.
2)
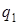
| 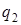
| 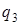
| 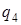
| 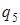
| 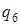
| ||
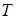 : :
| 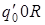
| 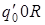
| 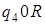
| 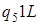
| 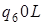
| 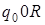
| |
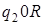
| 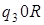
| 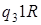
| 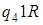
| 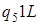
| 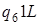
|
а) 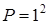 ; б)
; б) 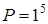 .
.
В Ответы и указания.
В Содержание.
Ответы и указания.
Глава 1. Высказывания, формулы, тавтологии. 2. 2), 5), 8), 10) – истинные высказывания. 1), 4), 7) – ложные высказывания. 3), 6) высказываниями не являются. 3. Обратите внимание, что 7) – составное высказывание. 5. Не являются тавтологиями: 2), 3), 5). Вернуться в Задачи.
Глава 3. Исчисление высказываний. 1. 1), 2), 5), 7), 8), 9) – формулы исчисления высказываний. 3), 4), 6), 10) формулами исчисления высказываний не являются. 2. 2). 3. 5) Применить лемму. 6), 7), 9) – применить результат 5). 8), 10), 11), 12) – применить результат 9). Вернуться в Задачи.
Глава 5. Предикаты. 1. 1) 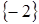 . 3)
. 3) 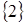 . 5)
. 5) 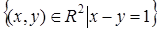 . 7)
. 7) 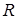 . 8)
. 8) 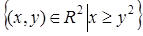 . 9)
. 9) 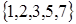 . 10)
. 10) 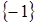 . 2. 1), 3), 4), 6), 7), 9), 10). 1. 2), 5), 8). 0. 3. 7) Воспользоваться формулой
. 2. 1), 3), 4), 6), 7), 9), 10). 1. 2), 5), 8). 0. 3. 7) Воспользоваться формулой 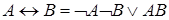 .
.
4. 1) 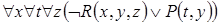 .
.
2) 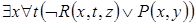 . 3)
. 3) 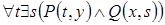 .
.
4) 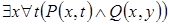 . 5)
. 5) 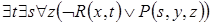 .
.
6) 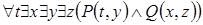 . 7)
. 7) 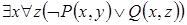 .
.
8) 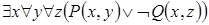 .
.
9) 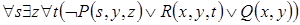 .
.
10) 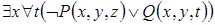 . 8. Можно привести такой пример:
. 8. Можно привести такой пример: 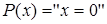 ,
, 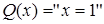 . Предикаты рассматриваются на множестве
. Предикаты рассматриваются на множестве 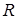 . Вернуться в Задачи.
. Вернуться в Задачи.
Глава 8. Рекурсивные функции. 1. 1) 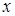 . 2)
. 2) 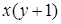 .
.
3) 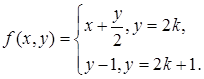 4)
4) 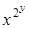 . 5)
. 5) 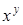 . 6)
. 6) 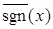 . 7)
. 7) 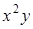 .
.
8)  9)
9) 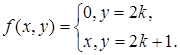
10) 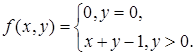 Вернуться в Задачи.
Вернуться в Задачи.
Глава 9. Машины Тьюринга. 1. 1) 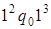 . 2)
. 2) 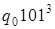 . 3)
. 3) 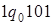 . 4)
. 4) 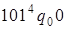 . 5)
. 5) 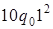 . 6)
. 6) 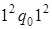 . 7)
. 7) 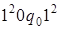 . 8)
. 8) 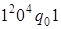 . 9)
. 9) 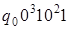 .
.
11) 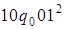 . 2. 1) а)
. 2. 1) а) 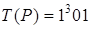 ; б)
; б) 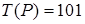 . 2) а) Неприменима;
. 2) а) Неприменима;
б) 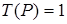 . 3) а); б) Неприменима. 4) а)
. 3) а); б) Неприменима. 4) а) 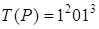 ; б) Неприменима. 5) а) Неприменима; б)
; б) Неприменима. 5) а) Неприменима; б) 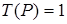 . 6. 1) а)
. 6. 1) а) 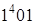 ; б)
; б) 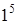 . 2) а)
. 2) а) 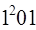 ;
;
б) 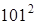 . 3) а)
. 3) а) 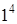 ; б)
; б) 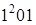 . 7. 1) а)
. 7. 1) а) 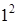 ; б)
; б) 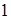 . 2) а)
. 2) а) 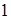 ; б)
; б) 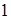 . Вернуться в Задачи.
. Вернуться в Задачи.
В Содержание.
Литература.
1. Бочкарева О.В. Учебное пособие по математике (специальные главы). М., Радио и связь, 2001.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. М., Наука, 1992.
3. Горбатов В.А. Фундаментальные основы дискретной математики. М., Наука, 2000.
4. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. М., Энергоатомиздат, 1988.
5. Кук Д., Бейз Г. Компьютерная математика. М., Наука,1990.
6. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М., ФИЗМАТЛИТ, 2001.
7. Логинов Б.М. Введение в дискретную математику. Калуга, 1998.
8. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. СПб, Лань, 1999.
9. Математическая энциклопедия. Т. 1. М., Советская Энциклопедия, 1977.
10. Мендельсон Э. Введение в математическую логику. М., Наука, 1984.
11. Непейвода Н.Н. Прикладная логика. Новосибирск, Изд-во Новосибирского университета, 2000.
12. Новиков Ф.А. Дискретная математика для программистов. СПб, Питер, 2000.
13. Тишин В.В. Теория алгоритмов, предикаты. Самара, 2001.
14. Фролов И.С. Элементы математической логики. Самара, Самарский университет, 2001.
15. Яблонский С.В. Введение в дискретную математику. М., Высшая школа, 2001.
В Содержание.
Дата добавления: 2022-02-05; просмотров: 863;











