Формальная арифметика.

Формальная арифметика – теория первого порядка со следующими специальными символами.

1) Предметная константа 0.

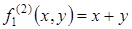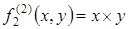2) Двуместные функциональные буквы и , одноместная функциональная буква .

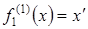3) Двуместная предикатная буква .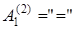

Собственные аксиомы следующие:

1) .

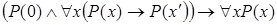2) .

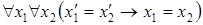3) .

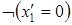4) .

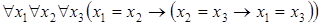5) .

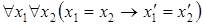6) .

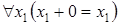7) .

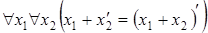8) .

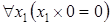9) .

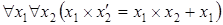Здесь 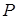– произвольная предикатная буква.

Теория частично упорядоченных множеств.

Теория частично упорядоченных множеств – это теория первого порядка с двумя предикатными буквами , .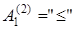

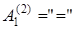Собственные аксиомы следующие:

1) .

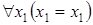2) .

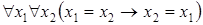3) .

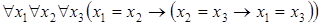4) .

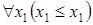5) .

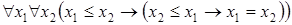6) .

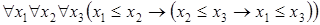Моделью данной теории является частично упорядоченное множество.

Для теорий первого порядка справедлива следующая теорема.

Теорема Гёделя о неполноте.Во всякой достаточно богатой теории первого порядка (в частности, во всякой теории, включающей формальную арифметику), существует такая истинная формула 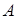, что 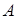ни , ни 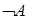не являются выводимыми в данной теории.

В Содержание.

Задачи.

1. Укажите, какие из следующих выражений являются формулами исчисления предикатов. В каждой формуле укажите свободные и связанные вхождения переменных:

1) .

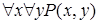2) .

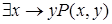3) .

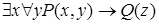4) .

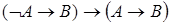5) .

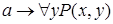6) .

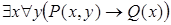7) .

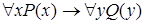8) .

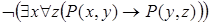9) .

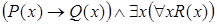10) .

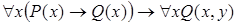2. Пусть 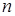– натуральное число. Даны следующие утверждения.

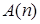· – “число 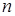кратно 5”;

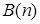· – “число 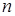кратно 2”;

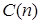· – “число 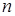кратно 4”;

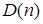· – “число 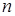кратно 10”;

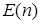· – “число 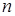кратно 20”.

Укажите, какие из следующих высказываний истинны, какие ложны.

1) .

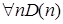2) .

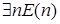3) .

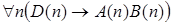4) .

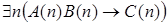5) .

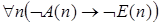6) .

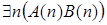7) .

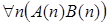8) .

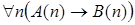9) .

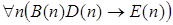10) .

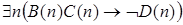3. Записать утверждения с помощью следующих обозначений: 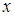, 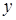– человек, 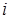– преподаватель Иванов, 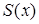– студент, 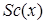– школьник, 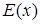– отличник, 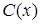– староста, 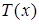– преподаватель, 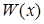– работающий, 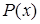– член профсоюза, 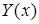– молодой, 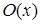– старый, 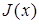– справедливый, 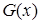– девушка, 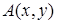– 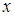боится .

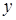1) Некоторые школьники и студенты – отличники.

2) Все старосты отличники и работают.

3) Все преподаватели и студенты являются членами профсоюза.

4) Не все молодые преподаватели справедливы.

5) Некоторые молодые и все старые преподаватели справедливы.

6) Все студенты и некоторые преподаватели молоды.

7) Среди работающих студентов есть отличники.

8) Некоторые студенты боятся преподавателя Иванова.

9) Никто из студенток не боится преподавателя Иванова.

10) Среди студенток-старост есть отличницы.

4. Построить систему собственных аксиом для следующих систем:

1) Линейное векторное пространство.

2) Группа (алгебраическая).

3) Метрическое пространство.

4) Семья.

5) Студенческая группа.

В Содержание.