СИСТЕМЫ СЧИСЛЕНИЯ МИКРОЭВМ. ДВОИЧНАЯ АРИФМЕТИКА. РАЗРЯДНЫЕ СЕТКИ. ПРЯМОЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
Системы счисления
Система счисления - это способ представления любого числа посредством некоторого алфавита символов. Различают непозиционные системы счисления (например, римская), позиционные (десятичная, двоичная, восьмеричная, шестнадцатеричная и др.) и системы с иррациональным основанием (коды Фибоначчи). Количество различных цифр в позиционной системе называют основанием системы S .
Любое число N в позиционной системе с основанием S представляется формулой
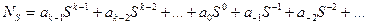 , (2.1)
, (2.1)
где k - количество цифр в числе N; a - любые из S цифр системы счисления.
Если найдено представление числа N в виде (2.1), то само число можно записать в виде:
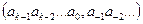 (2.2)
(2.2)
Например, если десятичное число выражается полиномом 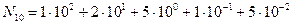 , то само число равно 125,1510.
, то само число равно 125,1510.
В двоичной системе счисления (2 с/с) используются только две цифры: 0 и 1; в восьмеричной (8 с/с) - восемь цифр: 0-7; в шестнадцатеричной (16 с/с) - десять цифр: 0-9 и шесть букв: А, В, С, D , Е, F. МикроЭВМ так же, как и другие ЭВМ, работают с информацией, представленной в 2 с/с.
Для связи оператора с микроЭВМ (для ввода и вывода данных, команд, адресов) используется 8 с/с (микроЭВМ типа DEC) или 16 с/с (микроЭВМ типа INTEL), так как в 2 с/с запись информации получается длинной и неудобной для оператора.
Перевод чисел из 10 с/с в другую позиционную систему с основанием S осуществляется по разным правилам для целой и дробной частей числа.
Перевод целых чисел. Для перевода целого числа из 10 с/с в систему с основанием (2 с/с, 8 с/с, 16 с/с) необходимо последовательно разделить это число и получаемые частные на основание S до тех пор, пока частное не станет меньше S. Запись числа производится, начиная с последнего частного, с присоединением остатков в последовательности, обратной их получению.
Пример. Перевести число 3310 в 2 с/с.
| - | |||||||||||
| - | |||||||||||

| - | ||||||||||
| - | |||||||||||
| - | |||||||||||

| |||||||||||
Запись. 3310 = 1000012 = 418 =2116.
Перевод дробных чисел. Для перевода дробной части из 10 с/с в систему S (2 с/с, 8 с/с, 16 с/с) необходимо умножить эту дробь и дробные части (без учета целых) получающихся произведений на основание S. Запись дроби производится с нуля с добавлением после запятой целых частей (сверху - вниз) получающихся произведений. Если при последовательном умножении после запятой не получаются нули, то перевод осуществляется с заданной точностью.
Пример. Перевести 0,62510 в 2 с/с.
| X | 0, | |
| X | 1, | |
| X | 0, | |
| 1, |
Запись: 0,62510 = 0,1012 = 0,58 = 0,A16.
В последней записи число 10 заменено символом А в соответствии со способом кодирования в 16 с/с (см. табл.2.1).
Перевод чисел из 10 с/с в 2 с/с можно производить, используя формулу (2.1), а также через 8 с/с или 16 с/с.
Очевидно, что основания 8 с/с и 16 с/с есть степени основания 2 с/с: 23 = 8, а 24 = 16. Следовательно, для записи каждой цифры восьмеричного числа необходимо три двоичных разряда (триада), а для представления каждой цифры шестнадцатеричного числа – четыре разряда (тетрада). Представление десятичных, восьмеричных и шестнадцатеричных целых чисел приведено в табл.2.1.
Перевод двоичных чисел в 8 с/с и 16 с/с. Производится путем разбиения двоичного числа на триады и тетрады соответственно влево и вправо от запятой с последующей заменой триад и тетрад на их символьные эквиваленты в соответствии с табл.2.1. Недостающие позиции в триадах и тетрадах заполняются нулями.
Таблица 2.1. Представление чисел.
| 10 c/c | 2 c/c | 8 c/c | 16 c/c |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Перевод чисел из 8 с/с и 16 с/с в двоичную. Производится заменой каждой цифры соответствующего числа двоичной триадой и двоичной тетрадой согласно таблице 2.1. Для дробных чисел можно написать аналогичную таблицу.
Пример. Перевести 10001,012 в 8 с/c и 16 с/c.
Запись: 010 001,0102 = 21,28
0001 0001,01002 = 11,416
Дата добавления: 2021-12-14; просмотров: 643;











