Параллелограмм (ромб)

Впервые с этими видами четырехугольников учащиеся знако­мятся в VII классе. Учитель предлагает школьникам из множества многоугольников отобрать только четырехугольники и объяснить, по каким признакам они это сделали. Затем из четырехугольников он просит выбрать только такие, у которых противоположные сто-

роны параллельны, и говорит, что такие четырехугольники назы­ваются параллелограммами (среди них будут прямоугольники, в том числе квадраты).

Далее рассматриваются элементы параллелограмма: стороны, углы. Учитель просит определить их количество и сообщает, что называние сторон любого параллелограмма такое же, как и сторон прямоугольника. Учащиеся показывают и называют верхнее и нижнее основания, боковые стороны, противоположные и смежные стороны.

Затем каждый ученик на своих моделях параллелограммов, среди которых будут и прямоугольники, должен установить свойства углов путем их совмещения. Учащиеся приходят к выводу, что противоположные углы параллелограммов (прямоугольников) равны.

Далее измеряются стороны параллелограммов (прямоугольни­ков). Оказывается, что в одних параллелограммах только противо­положные стороны равны, а в других — все стороны равны. «Па­раллелограмм, у которого все стороны равны,— сообщает учитель,— называется ромбом». Среди ромбов окажутся и квадраты.

В параллелограммах учащиеся проводят диагонали.

Путем неоднократного измерения устанавливается свойство диа­гоналей параллелограмма.

Высота в параллелограмме (ромбе) проводится внутри фигуры, т. е. из точки (вершины параллелограмма) опускается перпендику­ляр на противоположное основание.

В старших классах, начиная с VII, целесообразно работать над родовыми и видовыми понятиями. С этой целью учитель предла­гает школьникам модели многоугольников и просит:

а) отобрать четырехугольники;

б) среди четырехугольников выбрать все параллелограммы;

в) из параллелограммов выделить сначала прямоугольники, а уже из них квадраты или из параллелограммов выделить ромбы, а из них квадраты.

Учащимся предлагается измерить длину сторон параллелограм­ма и установить, является ли он ромбом, определить вид углов в параллелограмме и установить, является ли он прямоугольником. В VII классе основное внимание следует уделить классифика­ции многоугольников. Среди множества многоугольников выделя­ются сначала фигуры с наибольшим количеством углов, затем все меньшим и меньшим. Наконец, отбираются четырехугольники (четыре вершины, четыре угла, четыре стороны). Среди них дети выделяют параллелограммы — Четырехугольники с попарно параллельными сторонами. Оказывается, что в эту группу входят прямоугольники, и квадраты, и ромбы, и любые другие параллелограммы. Среди параллелограммов выделяются две группы: группа параллелограммов с равными сторонами (ромбы) и группа параллелограммов с прямыми углами (прямоугольники). Прямоугольники разделяются на две группы: прямоугольники и их частный вид — квадраты. Ромбы — на ромбы и квадраты. Учащимся будет легко проводить сравнение фигур, если они будут

пользоваться единой схемой, где указана последовательность сравне­ния фигур.

Схема классификации фигур в теме «Многоугольники».

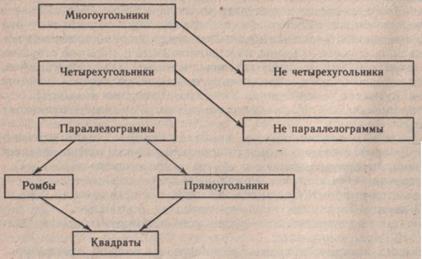
Для того чтобы учащиеся лучше понимали зависимость между известными им родовыми и видовыми понятиями, необходимо из­готовить таблички с названиями фигур и проводить с ними различные упражнения, например располагая таблички в соответствии со схе­мой сверху вниз, снизу вверх.

Однако не все учащиеся могут справиться с полной классифи­кацией всех многоугольников, устанавливая отношения иерархии между ними. Таким учащимся предлагается работать с этой схемой по частям. Например, учитель кладет табличку со словом «много­угольники», под ней учащиеся должны положить таблички со сло­вами «четырехугольники», «не четырехугольники», или учитель про­сит положить табличку со словом «параллелограмм», а под ней уча­щиеся кладут таблички с названиями фигур, относящихся к парал­лелограммам.

Построение параллелограмма

Для наиболее подготовленных учащихся начиная с VII класса может быть доступным построение любого параллелограмма с по­мощью транспортира.

Задача. Построить параллелограмм ABCD, если AD=9 см, 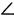А = 30 ⁰ , 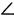D = 150°, AB = 6 см.

Построение параллелограмма по заданным элементам проводит­ся в таком порядке: 1) на произвольной прямой от точки А откла­дывается сторона AD (AD=9 см); 2) в точке А на стороне AD строится А ( А = 30°); в точке D на стороне AD строится

D( D =150°); 3) на проведенных лучах откладываются еще две стороны параллелограмма (AB = DC=6 см); 4) точки В и С соеди­няются отрезком.

Параллелограмм может быть построен по двум сторонам и одному углу: 1) на произвольной прямой от точки А откладывается данная сторона AD (AD = 8 см); 2) в точке А строится A ( A =40°); 3) на стороне угла, не принадлежащей прямой, от точки А откладывается вторая данная сторона АВ (АВ = 6 см); 4) через точку В проводится прямая, параллельная AD; 5) на ней откладывается длина стороны ВС (BC=AD = 8 см); 6) точки С и D соединяются отрезком.

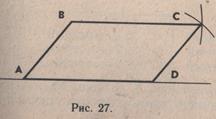
Следующий способ построения параллелограмма опирается на умение школьников строить треугольник с помощью циркуля. Уча­щиеся, зная длину сторон и величину одного из углов параллело­грамма, строят данный угол ( А) и от его вершины на сторонах угла откладывают данные отрезки (АВ и АD). Затем из конца одного отрезка (точки В) проводят с помощью циркуля дугу радиусом, равным второму отрезку, а из конца другого отрезка (точки D) — дугу радиусом, равным первому отрезку. Точка пересечения дуг (точка С) является недостающей четвертой вершиной паралле­лограмма (рис. 27).

Для построения любого ромба достаточно знать длину его стороны и величину какого-либо угла. Все этапы построения такие же, как и при построении любого параллелограмма.

В классе, где детям оказываются доступными работы, подобные вышеописанным, могут быть изучены углы, образующиеся в четырех­угольниках при пересечении диагоналей. Например, учащиеся вы­черчивают параллелограмм (ромб) и проводят в нем диагонали. Учитель просит учащихся сказать, сколько углов образовано при пересечении диагоналей, и установить с помощью транспортира, какова их величина (в градусах). Учащиеся должны определить, как делятся диагонали в точке пересечения.

Построение ромба и квадрата

Для построения ромба и квадрата можно воспользоваться свойст­вом диагоналей этих фигур: диагонали каждой фигуры в точке пересечения делятся пополам и образуют четыре прямых угла.

В точке пересечения диагонали квадрата делятся на четыре равных отрезка. В точке пересечения диагонали ромба делятся на попарно равные отрезки.

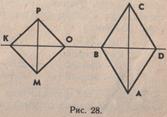
Строим две взаимно перпендикулярные прямые, от точки их пересечения отложим равные отрезки, концы этих отрезков соеди­ним. Получится квадрат (рис. 28). Проверим это, измеряя стороны и углы построенного четырехугольника.

Для построения ромба также воспользуемся свойствами его диагоналей. Сначала построим две взаимно перпендикулярные пря­мые и от точки их пересечения отложим на одной прямой два попарно равных отрезка и на другой прямой два других попарно равных отрезка. Соединим концы этих отрезков. Получим ромб. Проверим результат построения измерением. Измерим стороны — они равны и противоположные углы равны, следовательно, построен­ная фигура — ромб.

Треугольники

В Iклассе учащиеся учатся выделять треугольники сначала по образцу, затем знакомятся с названием этих фигур, выбирают треугольники из множества фигур по названию.

Во II классе они учатся вычерчивать треугольники с помощью линейки по точкам (вершинам).

В III классе из множества многоугольников школьники должны уметь выделять только треугольники. Учащимся будет легче за­помнить название элементов треугольника, если учитель напомнит, что это уже известные им названия. Таких элементов будет по три: три вершины, три угла, три стороны (основание и две боковые).

При изучении треугольников следует широко использовать их моделирование из трех планок.

Виды треугольников в зависимости от величины их углов

В V классе для каждого ученика необходимо заготовить набор треугольников (не менее трех), отличающихся величиной углов. С помощью чертежного треугольника они определяют виды углов этих треугольников. Модели треугольников и углы в них нумеруются. Если даны чертежи треугольников, то учащиеся обозначают вершины треугольников буквами. Последовательно прикладывая чертежный треугольник к углам фигуры, учащиеся записывают название вида угла. Например:

∆ № 1 ∆ № 2 ∆ № 3

1 — острый 1 — острый 1 — острый

2 — прямой 2 — острый 2 — острый

3— острый 3— острый 3— тупой

Учитель дает определение: «Треугольник, в котором один угол прямой (два других острые), называется прямоугольным треуголь-

ником». Аналогично учащиеся подводятся к определению других видов треугольников (остроугольного и тупоугольного).. Под соот­ветствующими номерами они записывают их названия: ∆ № 1 — прямоугольный, ∆ № 2 — остроугольный, ∆ № 3 — тупоугольный. После знакомства с прямоугольным треугольником необходимо дать его сопоставление с прямоугольником, так как сходство в произношении этих терминов приводит к их слабой дифферен­циации.

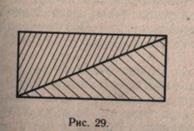
Эти фигуры надо сразу сопоставить, показать сходство и разли­чие. Следует образовать из прямоугольника два прямоугольных треугольника путем проведения в нем диагонали и записать: ABCD — прямоугольник; ABC, ACD — прямоугольные треугольники (рис. 29).

Даются задания: разрезать прямоугольник так, чтобы получи­лось два прямоугольных треугольника; а затем из этих треугольни­ков составить прямоугольник.

Здесь же необходимо рассмотреть вопрос о количестве прямых и тупых углов в прямоугольном и тупоугольном треугольниках. Учитель предлагает на произвольной прямой отложить отрезок — основание (любой длины) и с помощью чертежного треугольника построить прямые углы при концах основания (или два тупых угла). Учащиеся видят, что две стороны прямых углов не могут пере­сечься, а, следовательно, и треугольник не может образоваться. Две стороны тупых углов при тех же вершинах расходятся в раз­ных направлениях. Они тем более не могут пересечься и образовать треугольник. Значит, в треугольнике может быть только один пря­мой (тупой) угол, а два других — острые. Учитель задает такие вопросы: «Если в треугольнике один угол прямой, то какие будут два других угла? Как называется такой треугольник? Почему?»

Умственно отсталые учащиеся не могут вообразить или интуитив­но почувствовать, что не может быть треугольника с двумя или со всеми прямыми (тупыми) углами. В этом их надо убеждать, и не раз.

Виды треугольников в зависимости от длин их сторон

Для знакомства с видами треугольников по соотношению длин сторон каждый ученик получает треугольники двух видов: разно-

сторонний и равнобедренный. Предлагается измерить стороны этих треугольников и записать их длины. Например, учащиеся запи­сывают: ААВС, АВ = 5 см, ВС = 6 см, АС=8 см.

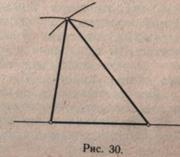
Учитель сообщает, что треугольники с разными по длине сто­ронами называются разносторонними треугольниками (рис. 30).

Измеряются стороны другого треугольника и записываются их длины. Устанавливается, что у него равны две боковые стороны, а третья имеет другую длину — это равнобедренный треугольник.

Учащиеся измеряют стороны различных треугольников на мо­делях и чертежах и определяют вид треугольника. В ходе этих упражнений выясняется, что среди равнобедренных есть треуголь­ники, у которых все стороны одинаковы. Ученики узнают, что такие равнобедренные треугольники называются равносторонними.

Необходимо показать учащимся использование треугольников с разной длиной сторон в технике, в быту.

В качестве упражнений учащимся предлагаются два вида за­даний: 1) измерить стороны треугольника, записать результаты измерения, определить вид треугольника; 2) известны длины всех трех сторон треугольника, определить его вид.

Построение треугольников

Когда дети будут свободно владеть классификацией треуголь­ников по длине сторон, можно перейти к их построению с помощью

циркуля и линейки.

Учитель делает на доске запись: АВ = 5 см, ВС = 6 см, АС=8 см, и сообщает, что он записал длины сторон треугольника. Ученики должны определить вид этого треугольника. Далее учитель говорит, что надо построить треугольник со сторонами данной длины (V класс).

Для построения нужно провести произвольную прямую. Одна из данных сторон принимается за основание будущего треугольника. Чтобы сохранить привычные обозначения вершин треугольника, за основание принимается сторона АС = 8 см. Отрезок, равный 8 см, откладывается циркулем на прямой и обозначается буквами. Затем раствором циркуля, равным 5 см (АВ = 5 см), из точки А как из центра проводится дуга, а раствором циркуля, равным 6 см (ВС = = 6 см), из точки С как из центра проводится вторая дуга. Точка пересечения дуг обозначается буквой В, точка В соединяется отрезками с точками А и С. Учащиеся проверяют правильность построения треугольника путем измерения сторон. Под чертежом они делают запись: АВ — 5 см, ВС = 6 см, СА=8 см. ∆ АВС — разносторонний (рис. 30).

При построении равнобедренного и равностороннего треуголь­ников последовательность и приемы работы остаются теми же.

Теперь, рассматривая каждый из треугольников, ученики должны уметь определить вид треугольника и по виду углов, и по длине сторон. Например, если дан ∆ АВС, учащиеся сначала с помощью учителя, а затем самостоятельно должны измерить его стороны, определить виды его углов и сделать такие записи:

∆ АВС

АВ = 6см 5 мм А — острый

ВС = 6 см 5 мм B — острый

С А = 7 см C — острый

∆ АВС -- равнобед- ∆ АВС — остро-

ренный угольный

Следовательно, АВС равнобедренный и остроугольный. Та­ким образом, каждый из треугольников получает два названия: по длине сторон и по виду углов.

Учащимся нужно предлагать треугольники разных видов — как по длине сторон, так и по виду углов. Работа по построению треугольников должна чередоваться с работами по измерению сторон и определению величины углов на моделях или чертежах треуголь­ников.

В VII классе учащиеся знакомятся с построением треугольника по данной длине двух сторон и величине угла между ними.

Дано: АВ и АС — стороны треугольника, A = 45°.

Построить: ∆ АВС.

Первый способ построения треугольника: 1) с помощью транспортира строим угол А, равный 45°; 2) откладываем на сторонах угла с помощью циркуля отрезки АВ и АС; 3) точки С и В соединяем, получаем ∆ АВС.

Стороны могут задаваться не только геометрически в виде отрезков, но и с указанием их длин.

В VII классе учащиеся также знакомятся с построением тре­угольника по стороне и двум прилежащим к ней углам с помощью транспортира. Например, дано: АС — сторона треугольника, А = =70^о, В =80^o. Построить ∆ АВС.

Построение: 1) на произвольной прямой откладываем отре­зок АС; 2) с помощью транспортира в точке А, справа от нее, строим A = 70°, а в точке С, слева от нее,— C = 80°; 3) продол­жаем стороны углов до пересечения, получаем треугольник АВС.

Второй способ построения треугольника: I) на произвольной прямой откладывается одна из данных сторон треугольника (AM = 10 см); 2) в точке А, справа от нее, строится данный угол ( А = 70°); 3) на стороне угла, не принадлежащей проведенной вначале прямой, от точки А откладывается вторая данная сторона (АD = 8 см); 4) точки М и D соединяются отрезка­ми, ADM построен, его размеры (две стороны AM и AD и угол, «включенный между ними) соответствуют условию задачи.

В каждом классе (V—IX) учитель должен давать задание на построение треугольника, равного данному. Сначала выясняется, что нужно знать, чтобы построить такой треугольник: при построении треугольников разных видов .(равностороннего, равнобедренного, разностороннего) нужно определить, сколько и какие данные необхо­димы для построения и почему.

Высота треугольника

В VI классе дети изучают перпендикулярные прямые, значит, их можно познакомить с высотой треугольника. Одни треугольники выше, другие — ниже. Установить это можно не всегда, а только в том случае, когда основания треугольников принадлежат одной пря­мой. Если треугольники расположить не на одной прямой, то сравнить треугольники по высоте без измерения ее будет трудно. Для этого надо определить расстояние, на котором находится вершина от основания. Расстояние измеряется по перпендикуляру (учащееся должны вспомнить, как определяется расстояние от точки до пря­мой).

Учитель сообщает учащимся, что высота в треугольнике — это перпендикуляр, опущенный из вершины треугольника на основа­ние или на продолжение основания. Сначала показывается уча­щимся чертеж остроугольного треугольника и высота в нем. Затем предъявляется прямоугольный треугольник с прямым углом при основании. Учитель просит отыскать высоту в этом треугольнике. Учащиеся приходят к выводу, что в прямоугольном треугольнике высота совпадает со стороной прямого угла.

Далее предъявляется чертеж тупоугольного треугольника. В нем высота — это перпендикуляр, опущенный из вершины на продолже­ние основания.

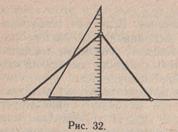
Наконец, надо познакомить школьников с построением высоты в треугольнике (рис. 31 и 32). Им надо показать, что построение высоты в треугольнике сводится к построению перпендикуляра из точки к данной прямой, т. е. к уже известному им способу построения. Тем не менее учитель объяснение построения высоты проводит сначала в остроугольном треугольнике. Например, дан ∆ АВС— остроугольный. Требуется построить высоту. Построение:

1) сторону прямого угла чертежного треугольника приложить к основанию АС данного треугольника так, чтобы вторая его сторона прошла через вершину В;

2) провести из вершины В перпендикуляр к основанию АС; он пересечет основание в точке D. Отрезок BD — высота АВС. В этом учащиеся могут убедиться, определяя виды углов BDC и BDA.

Наибольшую трудность у школьников вызывает построение вы-

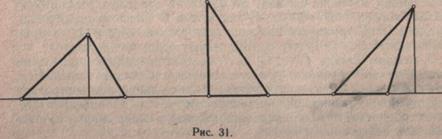
соты в тупоугольном треугольнике, так как высота в этом случае пересекает не основание, а его продолжение. Если дан тупоуголь­ный треугольник (с тупым углом при основании), то учитель по­казывает, что провести высоту на его основание невозможно. Следо­вательно, нужно продолжить основание и провести высоту на его продолжение. На первых порах ученики затрудняются самостоя­тельно продолжить основание, поэтому целесообразно чертить тре­угольник на произвольной прямой, где основание уже имеет продолжение. Учащиеся убеждаются в том, что перпендикуляр (высота треугольника) проходит вне треугольника, и подводятся к выводу: «Высота — это перпендикуляр, опущенный из вершины треугольника на основание или на продолжение основания». Необ­ходимо чаще требовать от учащихся построения высоты в треуголь­никах разных видов, сравнения треугольников по высоте. В этом случае школьникам придется строить высоты, измерять их, произ­водить разностное сравнение полученных чисел.

Сумма углов треугольника

Учащиеся VII класса должны по возможности самостоятельно прийти к выводу, что сумма углов треугольника любого вида равна 180°.

Методика подхода к такому выводу может быть различной. В одном классе можно идти дедуктивным путем — сообщить сразу, что сумма углов любого треугольника равна 180°. Затем убедить учащихся в этом на чертежах или моделях треугольников разного вида. Ученики последовательно измеряют углы с помощью транс­портира, находят их сумму, устанавливают вид треугольника по виду углов или длине сторон и подтверждают правильность поло­жения, высказанного учителем.

В другом классе можно использовать индуктивный путь — каж­дый ученик получает по 2—3 треугольника, измеряет углы каждого треугольника, находит их сумму. В результате в тетрадях возникает, например, такая запись: в ∆ ABC 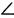A =45°, 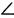В = 90°, 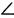C = 45°. Сумма углов в ∆ АВС равна 45°+45°+90° = 180°.

На основании практической работы, проделанной учащимися всего класса, они приходят к выводу о сумме углов в треугольнике.

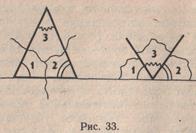
Для проверки правильности этого вывода может быть осущест­влена еще одна практическая работа. Школьники чертят разверну­тый угол с вершиной в точке О. Выполняют на листе бумаги чертеж треугольника (чертят треугольники разных видов). Вырезают треугольник, разрезают на три части, т. е. отделяют друг от друга все три угла. Затем помещают полученные модели углов последо­вательно внутрь развернутого угла так, чтобы их вершины совпадали с вершиной развернутого угла. Школьники видят, что углы треуголь­ника заполняют полностью внутреннюю область развернутого угла, г. е. их сумма равна 180° (рис. 33).

Далее проводятся различные упражнения с треугольниками раз­ных видов. Например, такие:

Учитель предлагает сравнить углы равностороннего треуголь­ника. Получив готовый чертеж (или выполнив его), учащиеся накладывают на один из углов прозрачный лист бумаги, обво­дят угол, а затем угол на бумаге совмещают с двумя другими углами треугольника. Делается вывод о равенстве углов равно­стороннего треугольника. Затем учащиеся измеряют углы этого треугольника с помощью транспортира. Результаты измерения по­казывают, что градусная мера каждого угла — 60^е. Вычислив сумму трех углов, школьники получают 180°.

1) Учащимся раздается чертеж равнобедренного треугольника. Они измеряют углы и устанавливают равенство углов при основа­нии (прилежащих к основанию). Находят сумму углов треугольника.

2) Измеряются углы разностороннего треугольника. Учащиеся приходят к выводу, что все они разной величины, а сумма углов равна 180°.

В дальнейшем знание суммы углов в треугольнике помогает детям установить точность произведенных ими измерений углов треугольника.

В VII классе учащиеся решают задачи вида:

1) Чему равна градусная мера каждого из углов равносторон­него треугольника и почему? (180°: 3.)

2) Угол при вершине равнобедренного треугольника равен 80°. Чему равен каждый из двух других углов? Какова градусная мера других двух углов? (180° —80° = 100°; 100°:2 = 50°.)

3) В разностороннем треугольнике ∆ ABC 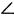A=50°, 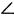B = 70°. Вычислить градусную меру 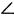C. (50°+ 70°= 120°; 180° - 120° = 60°.)

4) В ∆ АВС 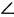А = 35°, 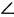B в 2 раза больше, 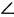C — ? (35°-2 = = 70°; 70° + 35° = 105°; 180°-105° = 75°.)

5) В ∆ АВМ 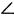В в 3 раза больше, чем 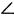A, a 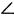C в 2 раза больше, чем 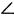A. Чему равна градусная мера каждого угла треуголь­ника? ( 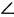А = 1 ч.; 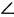В = 3 ч.; 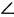C=2 ч.; I ч. + З ч. + 2 ч. = 6 ч.; 180°: 6 = 30°; 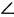А=30^o; 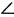В = 30° * 3 = 90°; 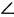C = 30° - 2 = 60°.) ∆ ABC — прямоугольный разносторонний.

6) В ∆ АВС 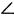А = 45°; 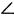В на 15° больше, чем 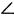А, 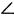С — ? (45° + 15° = 60°; 45° + 60° = 105°; 180°-105° = 75°.) И т. д.

Зная, чему равна сумма углов треугольника, школьники могут по-новому рассмотреть вопросоколичестве прямых и тупых углов

в треугольнике. Например, можно установить, что нет треугольника с двумя углами по 90°, так как сумма двух углов треугольника уже равна 180°.

Если один угол больше 90°, то второй и третий углы не могут содержать 90° или больше. Значит, в тупоугольном треугольнике может быть только один тупой угол.