Марковские модели в теории вычислительных систем.

Марковским называется случайный процесс, состояния которого в определенный момент времени t + δ зависят только от текущего состояния в момент времени t и не зависит от предыстории процесса, т.е. состояний, в которых пребывал процесс до момента t.

При описании реальных процессов с помощью марковских, можно, во-первых, пренебречь предысторией процесса, если это возможно, либо включить факторы, влияющие на состояния процессов в момент времени t, как параметры настоящего времени.

В класс марковских процессов выделяются процессы с дискретными состояниями, такие процессы называются марковскими цепями.

Если количество состояний в марковской цепи ограничено, то такая цепь называется конечной и состояние S={S₁, S₂, …, S_k} конечно.

Конечная марковская цепь может быть определена в непрерывном времени, когда система переходит из одного состояния в другое в произвольный момент времени t, и может быть определена на дискретном времени, когда переход из одного состояния в другое осуществляется в строго ориентированные моменты времени 1, 2, 3…

Соответственно конечная марковская цепь будет называться непрерывной либо марковской дискретной цепью.

Чтобы задать дискретную марковскую цепь нужно определить:

1). множество состояний системы S

2). задать матрицу вероятностей перехода из одного состояния в другое:

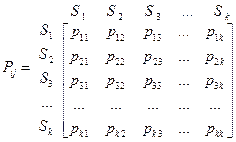
3). задать вектор начальных вероятностей

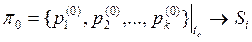
определяющий вероятность нахождения в момент времени t₀ системы состояний S_i.

Пример:

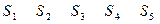
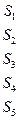
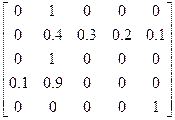
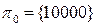
Функционирование данной марковской цепи может быть представлено в виде графа. Вершины – состояния в некоторый момент времени. Дуги – вероятность перехода из одного состояния в другое.

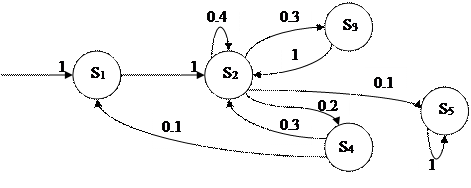
Таким образом, марковская цепь порождает множество реализации случайного процесса, который представляется последовательностью состояний S, соответствующей моменту времени 0, 1, 2…

Марковские цепи могут классифицироваться в зависимости от возможности перехода из одного состояния в другое.

В этой классификации основными разновидностями являются поглощающие и эргодические цепи.

Поглощающие марковские цепи содержат некоторое поглощающее состояние, достигнув которого процесс уже никогда его не покидает, т.е. по сути дела он прекращается.

Для задания такого процесса

p₀₀=1, p_0j=1

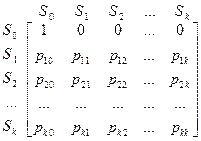
Из какого бы состояния не проистекал процесс, существует вероятность =1, что он окажется в поглощающем состоянии.

Основными характеристиками случайного рождаемого поглощающей марковской цепью является:

1). число пребываний процесса в состояниях S₁…S_k до момента поглощения,

2). число пребываний в каждом из состояний S_i, i=1..k на всем множестве состояний.

Это случайная величина со своим законом распределения, мат. ожиданием и дисперсией.

Поглощающие марковские цепи широко используются в вычислительных системах в качестве временных моделей программ и вычислительных процессов.

При моделировании программ состояние цепи отождествляется с блоками программы, а матрица переходов отождествляется с порядком переходов между блоками.

Этот порядок определяется структурой программы, входными данными, распределением ресурсов и т.д.

В результате такого представления можно вычислить число обращений к блокам программы, а также время выполнения программы, которые будут носить статистический характер и определяться своими характеристиками – мат. ожиданием, дисперсией и в сл. необходимым законом распределения.

Вычислительный процесс, сводящийся к последовательности обращения к ресурсам, которая определена программой, можно представить поглощающей марковской цепью, состояния которой соответствуют состояниям ресурсов системы, например процессора, памяти, либо периферийных устройств. В этом случае переходные вероятности отображают порядок обращения к различным ресурсам.

Эргодические марковские цепи представляют собой множество состояний, связанных матрицей переходных состояний, т.о. что из какого бы состояния процесс не проистекал, после некоторого числа шагов он мог оказаться в любом другом состоянии.

Т.о. процесс, начавшись в одном состоянии, никогда не прекращается, а последовательно переходит из одного состояния в другое, попадая в различные состояния с различной частотой.

Основной характеристикой эргодической цепи является вероятность пребывания процесса в состоянии S_j(j=1..k).

Эта вероятность определяет долю времени, которую процесс проводит в каждом из состояний. Используя эту характеристику можно определить загрузку.

Эргодические цепи могут использоваться в качестве модели надежности.

Состояния системы, различающиеся составом исправленного и неисправленного оборудования, могут трактоваться, как состояния эргодической цепи.

Переходы между состояниями могут трактоваться как отказы и восстановления, а также как реконфигурации связи между устройствами.

Оценки, полученные в такой модели, могут дать данные о надежности систему в целом.

Лекция №13